Kezdőlap


Cím:	Torziós jelenségek és méréstechnikai alkalmazásaik
Szerző(k):	Keglevich László
Füzet:	1964/december, 225 - 231. oldal	PDF \| MathML
Témakör(ök):	Szakmai cikkek

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Gyakran megfigyelhető hosszú zsinóron függő testeken, így pl. darukon lógó terheken, súlyosabb csillárokon, hogy felfüggesztő zsinórjuk körül lassú forgásszerű lengőmozgást végeznek. Hasonló mozgást végez az ide-oda forgó játéktárcsa is, amelyet keménypapír korongból, vagy nagyobb átmérőjű gombból és rajta átfűzött kettős fonálból annak idején talán magunk is készítettünk. Először néhányszor megcsavartuk a tárcsát a kifeszített fonálpár körül, majd ütemesen húzogatva a fonál két végét, ismétlődő és váltakozó irányú forgómozgását felerősítettük és fenntartottuk. Akárhányszor látunk felnyitott óraszerkezetet, azonnal megragadja figyelmünket az ide-oda járó billegő kerék is. Az ilyen fajta mozgások megfigyelésének eredményét hasznosították ugyanis az órások, amikor az ismétlődő mozgást végző lengőinga helyett a hordozható órákba is beszerelhető lengőkereket, a billegőt alkalmazták.

1. ábra

E mozgásokkal szoros kapcsolatban van az a megfigyelés is, hogy pl. fúrók és még inkább fúrótornyok fúróhegyei a nagy csavaró igénybevétel folytán tengelyük körül jelentősen elcsavarodnak. Hasonló történik gépek tengelyes erőátvitelénél is. Tengelyek ilyenfajta, sokszor nem kedvező elcsavarodását a tervezőnek a méretezésnél megfelelően figyelembe kell vennie.
A két összefüggő jelenség beható vizsgálata olyan eredményekre vezetett, amelyek lehetővé tették a csavaró igénybevételnél a helyes méretezést, és igen érzékeny tengely körül lengő rendszerek és eszközök (pl. torziós ingák, galvanométerek) szerkesztését. Az utóbbiak széles körű alkalmazása pedig jelentős mértékben előbbre vitte a méréstechnika fejlődését.
Hogy ezen ún. torziós jelenségek lényegét és a jelenségen alapuló műszereket, ill. méréseket megértsük, vizsgáljuk meg először a csavaró igénybevétel tulajdonságait.

A csavaró igénybevétel

Ha egyik végén rögzített szilárd testet, pl. rudat, drótot, pálcát vagy szalagot hossztengelye körül kissé elforgatunk, a tengelyre merőleges szomszédos rétegek egymáshoz képest egyenlő mértékben elfordulnak. Az elfordulás szöge (

α

) elég kis szögelfordulás esetén (a rugalmasság határa alatt) a tapasztalat szerint arányos a működő forgatónyomatékkal (

F = P ϱ

), a szál hosszával (

l

), hengeres szál esetén fordítottan arányos az

r

sugár negyedik hatványával és függ az anyagi minőségtől:

2. ábra

\begin{matrix} α = β \frac{2 F l}{r^{4} π} . \end{matrix}

(1)

Itt

β

a csavarás rugalmassági együtthatója, amely anyagonként más és más. Használatos ennek reciprokra is, a torzió modulusz (

G

\begin{matrix} G = \frac{1}{β} . \end{matrix}

(2)

Az elforgatás során a szálban rugalmas feszültség ébred, amely az elforgatást akadályozni és az elforgató hatás megszűnése után az eredeti nyugalmi állapotot visszaállítani igyekszik. Ez a rugalmas feszültség a szomszédos rétegek részecskéinek összetartó erejéből származik és nagysága (1)-ből kifejezve:

\begin{matrix} F = \frac{1}{β} \frac{r^{4} π}{2 l} α . \end{matrix}

(3)

Mivel az elcsavart szálban ébredő rugalmas feszültség kismértékű elcsavarás esetén az elforgatási szöggel egyenesen arányos és az elcsavarást okozó forgatónyomatékkal ellenkező irányú, vagyis

F_{r} = - F

, így ez is harmonikus rezgőmozgás lineáris erőtörvényéhez hasonló

\begin{matrix} F_{r} = - D^{*} α \end{matrix}

(4)

lineáris forgatónyomaték-törvényt jelent. A

D^{*}

az ún. ,,direkciós forgatónyomaték'', amely az egységnyi szögelforduláshoz szükséges forgatónyomatékot jelenti, és esetünkben (3) alapján a szál adataival kifejezve:

\begin{matrix} D^{*} = \frac{1}{β} \frac{r^{4} π}{2 l} . \end{matrix}

(5)

Egy szál végére erősített test eszerint kis kitérítés után tengelye körül harmonikus rezgőmozgást, tehát periodikus forgómozgást, vagy a gyakorlati kifejezéssel élve, torziós lengést végez.

Torziós rendszerek

A legegyszerűbb ilyen torziós lengéseket végző eszköz egy vékony szálra függesztett keresztrúd, amelyre megfelelő módon testek erősíthetők. Az ilyen felépítésű eszközzel szögelfordulás, vagy a lengés lefolyásának megváltozása alapján kis erőhatások mérhetők. Az előbbi esetben torziós mérlegnek, az utóbbi esetben torziós ingának szokás nevezni. Ilyen eszközöket használt nagy jelentőségű méréseinél pl. Cavendish, Coulomb és Eötvös Loránd. Természetesen létrejöhet torziós lengés mindkét végén rögzített szál, vagy tengellyel rögzített, de spirál-rugóval torziós lengések végzésére alkalmassá tett test esetén is, mint pl. a feszített-szálas galvanométer, ill. az órák billegő kereke esetében. Az utóbbinál tulajdonképpen a spirál-rugó nem csavarási, hanem hajlítási igénybevételnek van kitéve. Biztonságos rugóvastagság esetén azonban így lehet csak kellő kis értékűvé tenni a rendszer torzió moduluszát.

A torziós lengések fontos jellemzője a lengésidő (

T

). Ennek mérésével meghatározhatjuk a lengőrendszer egyéb olyan jellemzőit, amelyek a lengésidővel összefüggésben vannak. Meg kell vizsgálnunk tehát, hogy a lengés mitől és milyen módon függ, továbbá meg kell állapítanunk ezen mennyiségek és a lengésidő között az összefüggést.

Párhuzam a haladó- és forgómozgás jelenségei közt

Kitűzött feladatunkat könnyen megoldhatjuk, ha megvizsgáljuk azt, hogy a csavarási igénybevétel és a torziós lengés milyen ismert jelenségekkel van analógiában.

4. ábra

Írjuk fel ezért a Hooke-törvény alapján valamely

l

hosszúságú,

q

keresztmetszetű és

ε

rugalmassági együtthatóval rendelkező pálcában az

y

hosszmenti megnyúlás vagy összenyomás esetén fellépő

P_{r}

ellenerő nagyságát:

\begin{matrix} | P_{r} | = \frac{1}{ε} \frac{q}{l} y . \end{matrix}

(6)

Ezt (3)-mal összehasonlítva könnyű észrevenni, hogy a csavarási igénybevétel a húzási-nyomási igénybevételnek a forgómozgásbeli megfelelője. Minthogy a pálcában fellépő ellenerő a kitéréssel arányos és azzal ellentétes irányú, ez éppen a harmonikus rezgőmozgás

\begin{matrix} P_{r} = - D y \end{matrix}

(7)

erőtörvényének felel meg. A rugalmas pálcában tehát egy hosszirányú

P

erőlökés esetén

\begin{matrix} D = \frac{1}{ε} \frac{q}{l} \end{matrix}

(8)

direkciós erő értékkel ugyanilyen irányú harmonikus rezgőmozgás jön létre. A forgómozgásnál ennek megfelelője a torziós lengés

(

(4), (5)

)

.
Tekintettel arra, hogy a harmonikus rezgőmozgásnál a rezgésidőt meg tudjuk határozni, próbáljuk párhuzamunkat továbbvinni, és a haladó mozgás összefüggéseibe a forgómozgás megfelelő mennyiségeit helyettesítve a lengésidőt a torziós lengés esetére ebből meghatározni. A harmonikus rezgőmozgás esetén a

D

direkciós erő a mozgástörvényből a következőképpen fejezhető ki:

\begin{matrix} D = m \frac{4 π^{2}}{T^{2}} . \end{matrix}

(9)

Ebből a rezgésidő

\begin{matrix} T = 2 π \sqrt[]{\frac{m}{D}} . \end{matrix}

(10)

Helyettesítsük ebbe (8) alapján a direkciós erőnek a pálca adataival kifejezett értékét és vezessük be itt is szokás szerint a rugalmassági együttható helyett az

E

rugalmassági moduluszt:

\begin{matrix} T = 2 π \sqrt[]{\frac{m l}{E q}} . \end{matrix}

(11)

Látható, hogy a rezgésidő arányos a hosszúság és a tömeg négyzetgyökével, továbbá fordítva arányos a keresztmetszet és az

E

rugalmassági modulusz négyzetgyökével. Az ilyenfajta pálca menti ún. longitudinális rezgések a hangtanban fontos szerepet játszanak.
Nézzük meg most, hogy a forgómozgás megfelelő mennyiségeit az előbbi összefüggésekbe helyettesítve hogyan kaphatjuk meg a lengésidőt. Először fejezzük ki (9)-hez hasonlóan a direkciós forgatónyomatékot a lengésidővel és az

I

tehetetlenségi nyomatékkal:

\begin{matrix} D^{*} = I \frac{4 π^{2}}{T^{2}} . \end{matrix}

(12)

Ebből a lengésidő

\begin{matrix} T = 2 π \sqrt[]{\frac{I}{D^{*}}} . \end{matrix}

(13)

Ha most a lengésidő képletében

D^{*}

-nak a rugalmas csavarásnál érvényes (5) értékét helyettesítjük (2) összefüggés felhasználásával, akkor a

\begin{matrix} T = 2 π \sqrt[]{\frac{2 I l}{G r^{4} π}} \end{matrix}

(14)

összefüggést nyerjük. Ez megadja egy torziós rugalmassága folytán periodikus forgómozgást végző test lengésidejét a test (inga) geometriai adatai, tehetetlenségi nyomatéka és torzió modulusza segítségével. Eszerint a

T

lengésidő a rendszer tehetetlenségi nyomatékának és a szál hosszának négyzetgyökével egyenesen, a szál sugarának második hatványával és a torzió modulusz négyzetgyökével pedig fordítottan arányos. Figyelemre méltó, hogy a sugár változásával igen érzékenyen változik a lengésidő. Pl. tízszer kisebb sugár esetén százszor nagyobb a lengésidő.
A párhuzam végigvitele eredménnyel járt, rendelkezésünkre áll a lengésidő képlete. A hasonlatot kiterjesztve az útképletre még beláthatjuk, hogy e mozgás útképlete is

sin

függvénnyel írható le. Azonban ennél többet is mondhatunk. Magasabb számítástechnikával igazolható, hogy bármilyen jelenség, amelynél a harmonikus rezgőmozgás erőtörvényéhez hasonló összefüggés érvényes, leírható

sin

függvénnyel, továbbá a rezgésidőre hasonló módon összefüggés nyerhető (pl. az elektromos rezgések feszültség-idő függése, a rezgőkörre vonatkozó Thomson-féle rezgésidő képlet).

Alkalmazások

Ezek után nézzük meg, hogy milyen feladatok megoldására alkalmas a torziós rendszer. Az egyik nagy terület az, ahol mint torziós mérleg használatos a kicsiny forgatónyomaték, ill. erők mérése. A mérleg érzékenységét növelhetjük azáltal, hogy elég kis szálkeresztmetszetű; nagy szakítószilárdságú anyagból készült szálat (pl. kvarc vagy platinaszálat) használunk, és a szögelfordulást tükrös leolvasással végezzük. A tükrös leolvasás úgy történik, hogy távcsővel nézünk a szálra erősített kicsiny tükörben egy skálát. Ilyen eszközzel lehet gravitációs, elektromos, mágneses, ill. súrlódási erőket mérni, vagy ezáltal más mennyiségeket is, mint pl. áramlási sebességet vagy elektromos áramot (galvanométerek). A tengelyes árammérő műszerek is ilyen áram hatására létrejövő és ezzel arányos szögelfordulást visznek mutatóra. Használatosak kicsiny tömegek mérésére is érzékeny torziós mérlegek, amelyek egy spirálrugóval egyensúlyozott, tengellyel rögzített karból állnak.

5. ábra

Ezen statikusnak nevezhető alkalmazások mellett a torziós inga lengésekkel kapcsolatos dinamikus alkalmazásai is jelentősek. Ezeknél időmérésre vezetjük vissza a mérni kívánt mennyiséget. A lengésidő mérésével ugyanis a (14) összefüggésben szereplő és a velük további összefüggésben álló minden mennyiség mérésére lehetőség nyílik. Ha figyelembe vesszük azt, hogy a lengésidő kisebb elfordulás esetén, akárcsak a harmonikus lengőmozgás esetében, független az amplitúdótól, akkor lehetővé válik, hogy a lengésidőt nagyszámú lengés együttes idejéből határozzuk meg. Így a több lengésidő együttes mérésénél elkövetett, de egy lengés mérésénél elkövetett hibával megegyező hibának csak egy része jut a lengésidőre, vagyis a lengésidő hibájának értéke annyiszor lesz kisebb, ahány lengésből meghatároztuk. Ezzel a mérni kívánt mennyiség mérési pontosságát jelentősen, a csillapodás okozta korlátig fokozhatjuk.

6. ábra

Torziós ingával nagy pontossággal mérhető a tehetetlenségi nyomaték és a torzió modulusz. Ezt a továbbiakban részletesen tárgyaljuk. Nagy pontossággal mérhetők ugyancsak az egyes kicsiny térerősségek lengésidő mérésével. Eötvös Loránd a gravitációs állandó mérésére dolgozott ki egy ilyen elven működő igen érzékeny eljárást. A nagyon finom drótszálon függő torziós ingát két ólomhasáb közé helyezte egyszer a hasábokat összekötő távolságra merőleges, majd ezzel párhuzamos egyensúlyi helyzetben. Mindkét esetre mérve a lengésidőt, a merőleges helyzetben nagyobb

T

értéket kapott, mivel a vonzóerő a kitérési szöget növelni igyekszik és ilyenkor a szál forgatónyomatékához hozzáadódik. Ez olyan, mintha a szál

D^{*}

direkciós forgatónyomatéka kissé lecsökkent volna. Párhuzamos esetben éppen ellenkező szerepe volt a hasáboknak. Az észlelt lengésidőkből és a geometriai adatokból a gravitációs állandó kiszámítható.
Alkalmazzák a torziós ingát a folyadékok folyékonyságára jellemző belső súrlódás mérésénél, ahol a forgástengelye körül lengetett hengerben levő folyadék fékező hatása a lengésidő megváltozásában jelentkezik. Különböző csillapítás-méréseknél szintén nélkülözhetetlen a torziós inga. Méréseredményeiből még az anyag szabályos felépítésétől való eltérésekre, a kristály-rácsszerkezetének hibáira is következtethetünk. Ilyen méréseknél a vizsgálandó anyagból készítik a nagy tömegű torziós inga szálát. Mindezeken túlmenően a módszer oly érzékennyé tehető, hogy vele a kicsiny fénykorpuszkulák becsapódásából eredő fénynyomás is mérhetővé válik (Lebegyev kísérlete). Az érzékenység itt a lengés ütemében történő periodikus megvilágítással igen nagy mértékben fokozható. Legmindennaposabb használata természetesen az egyszerű időmérésnél az időjelző órákban van, ahol a kis billegő kerék nem más, mint egy kis torziós inga, amelyet spirál rugó tesz a tengely körül lengőképessé. Az inga lengéseit egy számláló szerkezet, maga az óra számlálja, és az eredményt mutatóval jelzi. A hajszálrugók feszességének szabályozásával a

D^{*}

változtatása által elérhetjük azt, hogy óránk pontosan jár.

A torzió modulusz mérése

Az előbbi gondolatmenet során közelebbről megismertük a torziós jelenségeket, összefüggéseiket, ezek érvényességének feltételeit és az alkalmazásokat. Láttuk, hogy ezeknél a torziós tulajdonság jellemzésére a csavarás rugalmassági együtthatója, vagy még inkább ennek reciproka, a torzió modulusz szolgál. Érthető tehát, hogy ennek ismerete a különböző műszaki csavaró igénybevételeknél használt anyagok és torziós műszerek szálanyagainak helyes megválasztása szempontjából egyaránt fontos. Ezért az egyes anyagok torzió modulusz értékét az elérhető legnagyobb pontossággal már előre megmérik. Egységei a

{din/cm}^{2}

, a

{kp/cm}^{2}

, ill.

{kp/mm}^{2}

. A továbbiakban megvizsgáljuk, hogy milyen mérési módszerek kínálkoznak a torzió modulusz meghatározására.
Az (1) összefüggés torzió moduluszra kifejezett alakja,

\begin{matrix} G = \frac{2}{π} \frac{l F}{r^{4} α} \end{matrix}

(15)

csavaró igénybevétel alapján sztatikusan ad lehetőséget a meghatározásra. Ennél a geometriai adatokon kívül a működő forgatónyomatékot és a szögelfordulást is mérni kell. Az utóbbiak pontos mérése nehéz.
Meghatározható a torzió modulusz az anyagminta száljából készített torziós inga segítségével a (14)-ből nyert

\begin{matrix} G = 8 π \frac{l I}{r^{4} T^{2}} \end{matrix}

(16)

összefüggés alapján dinamikus módszerrel is, ha a torziós inga szálára akasztott test

I

tehetetlenségi nyomatéka ismert és ehhez képest a szál tehetetlenségi nyomatéka elhanyagolható. Ilyen mérésnél a geometriai adatokon kívül még a lengésidőt kell mérni. Az utóbbi óriási pontossággal mérhető, de a tehetetlenségi nyomaték a mérése és az elhanyagolás során adódó kisebb pontossága miatt a

G

érték pontosságát erősen korlátozza.
Akkor is meghatározható azonban torziós ingával a

G

, ha ismeretlen a test tehetetlenségi nyomatéka és nem hanyagolható el a szál tehetetlenségi nyomatéka sem. Az ehhez felhasználandó új összefüggéshez a forgómozgást végző test tehetetlenségi nyomatékának a tengely körüli tömegeloszlástól való függését leíró fontos szabály, a Steiner-tétel birtokában juthatunk el. A Steiner-tétel kimondja, hogy egy test valamely tengelyre vonatkoztatott tehetetlenségi nyomatéka megegyezik a szóban forgó tengellyel párhuzamos, súlyponton átmenő tengelyre vonatkoztatott tehetetlenségi nyomaték,

I_{0}

és a test e két tengelye közti távolság (

s

) négyzetével szorzott tömegének (

m

) összegével. Képletben:

\begin{matrix} I = I_{0} + m s^{2} . \end{matrix}

(17)

A tétel könnyen belátható, ha arra gondolunk, hogy egy merev test erő hatására úgy mozog, mintha súlyponton egyesített tömegére a súlypontban támadó erő működne. Az

I_{0}

súlyponton átmenő tengelyre vonatkoztatott tehetetlenségi nyomaték a test tömegeloszlásától függő állandó érték. Ha a tengely nem a súlyponton megy át, a mozgás szempontjából a súlypontba egyesítve képzelt össztömeg a súlyponttól

s

távolságra lévén

m s^{2}

tehetetlenségi nyomatékot jelent. Ehhez azonban még hozzá kell vennünk a valóságos tömegeloszlásból származó, súlyponton átmenő tengelyre vonatkoztatott

I_{0}

tehetetlenségi nyomatékot, és így épp a tételben kimondott összefüggést nyerjük.
E tétel birtokában keresünk tehát a torzió moduluszra összefüggést, amelyben

I

már nem szerepel. A gondolatmenet a következő. Két egyenlő

m

tömeget erősítünk ingánkra a forgástengelytől

s_{1}

távolságra és mérjük a

T_{1}

lengésidőt. Ezután a két tömeget

s_{2}

távolságra téve újra mérjük az ehhez tartozó

T_{2}

lengésidőt. A szál hosszának (

l

), sugarának (

r

) és ezen öt adatnak (

m

s_{1}

s_{2}

T_{1}

T_{2}

,) a mérésével a

G

már számolható.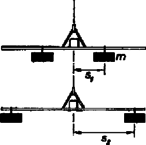

7. ábra

Az első esetben ugyanis az össz-tehetetlenségi nyomaték,

I_{1}

nem más, mint az üres inga tehetetlenségi nyomatékának (

I_{ü}

) és a tengelytől

s_{1}

távolságra levő

m

tömegek tehetetlenségi nyomatékának összege. Az utóbbi pedig a Steiner-tétel alapján az

m

tömegek súlypont körüli tehetetlenségi nyomatékának (

I_{m}

) és a súlypont-tengelytávolság (

s_{1}

) négyzetével szorzott tömegértékek összegezésével nyerhető.
Tehát

\begin{matrix} I_{1} = I_{ü} + 2 I_{m} + 2 m s_{1}^{2} . \end{matrix}

(18)

Ugyanígy a második esetben

\begin{matrix} I_{2} = I_{ü} + 2 I_{m} + 2 m s_{2}^{2} . \end{matrix}

(19)

és a két egyenlet megfelelő oldalainak különbsége

\begin{matrix} I_{2} - I_{1} = 2 m (s_{2}^{2} - s_{1}^{2}) . \end{matrix}

(20)

Ezen két esetben a lengésidő összefüggéseink négyzetének különbsége (14) szerint

\begin{matrix} T_{2}^{2} - T_{1}^{2} = \frac{4 π^{2} \cdot 2 l}{G r^{4} π} (I_{2} - I_{1}) . \end{matrix}

(21)

Az imént (20) meghatározott

I_{2} - I_{1}

különbséget ide helyettesítve

\begin{matrix} T_{2}^{2} - T_{1}^{2} = \frac{8 π l}{G r^{4}} \cdot 2 m (s_{2}^{2} - s_{1}^{2}) . \end{matrix}

(22)

Ebből

G

torzió moduluszt kifejezve nyerjük a keresett összefüggést:

\begin{matrix} G = \frac{16 π l m (s_{2}^{2} - s_{1}^{2})}{r^{4} (T_{2}^{2} - T_{1}^{2})}, \end{matrix}

(23)

amelyben már semmiféle tehetetlenségi nyomaték nem szerepel. Ehelyett megjelent a tömeg és az

s_{1}

, ill.

s_{2}

távolság, amelyek viszont jól mérhetők.

Keglevich László