Kezdőlap


Cím:	Néhány szó a reális gázokról
Szerző(k):	Vesztergombi György
Füzet:	1964/november, 161 - 166. oldal	PDF \| MathML
Témakör(ök):	Szakmai cikkek

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Mindenki ismeri a Linde-féle cseppfolyósítási eljárást, amely azon alapul, hogy a gázok kiterjesztéskor lehülnek. Tegyünk a készülékbe hidrogént. Várakozásunkkal ellentétben a komprimált hidrogén ahelyett, hogy kiterjesztéskor lehülne, felmelegszik. Vagyis a hidrogént ezzel a módszerrel nem lehet cseppfolyósítani. Ez az eredmény az első pillantásra nagyon meglepő. Úgy tűnik, mintha az energiamegmaradás törvényével jutottunk volna ellentétbe: nem tudjuk, honnan vette a gáz a felmelegedéshez szükséges hőenergiát. E probléma megoldásához kissé alaposabban meg kell ismerkednünk a gázok sajátosságaival.
A III. osztályos fizika tankönyvből ismeretes az egyetemes gáztörvény ideális gázokra, mely szerint $\frac{p V}{T} =$ konstans. Ezt az összefüggést a gázok molekulasúlynyi mennyiségére vonatkozóan $p V = R T$ alakban szokták írni, ahol $R = 8, 31 erg/fok \cdot mol = 8, 205 \cdot 10^{- 2} liter atm/fok \cdot mol$ , az univerzális gázállandó.
Ezen egyenlőség alapján azonban nem tudjuk megmagyarázni a fenti jelenséget, sőt még a közönséges gázok kiterjedésekor történő lehűlését sem, mert ha a $p V$ szorzat állandó, akkor $T$ -nek is állandónak kell maradnia. ‐ Viszont a legtöbb gáz mégis lehűl. Hova tűnik ekkor az energia?
Ez is azt bizonyítja, hogy mennyire eltérnek a reális gázok az ideális gáztól, amelyről feltételeztük, hogy a molekulái között nem hatnak erők, és a molekulák ütközéskor úgy viselkednek, mint elenyészően kis méretű abszolút rugalmas gömböcskék. Ezeknek a hibáknak a kiküszöbölésére állította fel Van der Waals holland fizikus a gázok általános állapotegyenletét. Ő mutatott rá arra, hogy az állapotegyenletben nem szabad a gáz rendelkezésére álló összes térfogattal számolni, hanem ebből le kell vonni a molekulák által betöltött $b$ térfogatot, vagyis a fenti egyenlet így módosul:
$(V - b) p = R T$ , ahol $b$ az anyagi minőségre jellemző állandó. Ebből a nyomásra a következő értéket kapjuk: $p = \frac{R \cdot T}{V - b}$ . A valóságban azonban a nyomás a molekulák közt fellépő vonzóerők miatt ennél valamivel kisebb. Ha ugyanis egy molekula a fal közvetlen közelében a fal felé halad, a szomszédai részéről kifejtett vonzóerők egy befelé irányuló erőt eredményeznek (gondoljunk csak a felületi feszültség analóg jelenségére), amely a falba ütköző molekula sebességét, impulzusát és ezzel együtt a falra gyakorolt nyomását is csökkenti. Ez a vonzóerő arányos a vonzó molekulák számával, ez pedig fordítottan arányos a térfogattal, ezért az egyes molekulákra kifejtett vonzás $\frac{a'}{V}$ alakban írható, ahol $a'$ állandó. A gáz felületegységre gyakorolt összes belső vonzása (vagyis a nyomás-csökkenés) a felületen levő egyes molekulákra kifejtett vonzásból adódik össze. Ezek száma azonban szintén fordítottan arányos a moltérfogattal: $\frac{a''}{V}$ , ahol $a''$ állandó. A molekulák kölcsönös vonzásából származó kohéziós nyomás $\frac{a'}{V} \cdot \frac{a''}{V} = \frac{a}{V^{2}}$ , ahol $a$ a gáz anyagi minőségére jellemző állandó.
Tehát az edény falára ható eredő nyomás: $p = \frac{R \cdot T}{V - b} - \frac{a}{V^{2}}$ .
Ezt rendezve kapjuk a Van der Waals-féle egyenletet:

\begin{matrix} (p + \frac{a}{V^{2}}) (V - b) = R T . \end{matrix}

Az állandók értékei néhány gázra:

\begin{matrix} a (\frac{{lit}^{2}}{{mol}^{2}} atm) & b (\frac{lit}{mol}) \\ Hidrogén & 0,245 & 0,0219 \\ Nitrogén & 1,345 & 0,0385 \\ Oxigén & 1,36 & 0,0318 \end{matrix}

A Van der Waals állapotegyenlet birtokában most már konkrét példákon is megmutathatjuk, hogy az egyes gázok hőmérséklete törvényszerűen megváltozik a nyomásváltozás hatására, mégpedig a gáz anyagi minőségétől függően. A következő kísérletet végezzük el. (Hogy a külső légnyomással ne kelljen törődnünk, képzeljük az egészet légüres térben.)

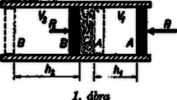1. ábra

Vegyünk egy jó hőszigetelő anyagból készült

q

keresztmetszetű csövet. Ezt egy porózus testtel, pl.

C

vattacsomóval két részre osztjuk. A cső két végét egy-egy ideális dugattyú zárja le. Az

A

és

C

közti részbe helyezzük a vizsgálandó adott hőmérsékletű gáz

1

molnyi mennyiségét. Hogy a két oldalon az állandó nyomást biztosítsuk, a dugattyúkra állandó

P_{1}

és

P_{2}

erővel hatunk. Legyen

P_{1} > P_{2}

, ekkor az

A C

részből, ahol nyomás

p_{1} = \frac{P_{1}}{q}

, a gáz eltolva a másik dugattyút, átáramlik a másik oldalra, ahol a nyomása

p_{2} = \frac{P_{2}}{q}

, a két rész közt a nyomás kiegyenlítődését a

C

vattacsomó, az ún. ,,fojtási hely'' akadályozza meg, ugyanis időegység alatt csak adott mennyiségű gáz áramolhat át rajta. Így ez a nyomáskülönbség mindaddig fennmarad, amíg az

A

dugattyú teljesen át nem nyomja a gázt. A folyamat eredménye az, hogy a teljes gázmennyiség

p_{1}

nyomásról

p_{2}

nyomású lett.
Mint az előbb említettük, a kísérlettel az volt a célunk, hogy a nyomásváltozás közben a gáz ne kapjon és ne is adjon le energiát. Teljes hőszigetelést feltételezve, munkavégzés csak a két dugattyúnál volt lehetséges. A jobboldalon nekünk kellett

L_{1} = P_{1} h_{1}

munkát végeznünk, míg a baloldalon a gáz végzett

L_{2} = P_{2} h_{2}

munkát. A gáz belső energiája akkor marad változatlan, ha

L_{1} = L_{2}

, vagyis

P_{1} h_{1} = P_{2} h_{2}

. Felhasználva a nyomás és nyomóerő közti összefüggést:

p_{1} q h_{1} = p_{2} q h_{2}

, és bevezetve a

q h_{1} = V_{1}

és

q h_{2} = V_{2}

jelöléseket, a

\begin{matrix} p_{1} V_{1} = p_{2} V_{2} összefüggést kapjuk. \end{matrix}

(1)

(Vigyázzunk, ez nem azonos a Boyle-Mariotte-törvénnyel, mert itt egy szóval sem említettük, hogy a két állapotban a hőmérséklet azonos, sőt éppen a hőmérséklet-változást keressük !)
Másrészt tudjuk, hogy a gázra mindkét állapotában érvényes a Van der Waals-egyenlet:

\begin{matrix} (p_{1} + \frac{a}{V_{1}^{2}}) (V_{1} - b) = R T_{1}, & (2) \\ (p_{2} + \frac{a}{V_{2}^{2}}) (V_{2} - b) = R T_{2} . & (3) \end{matrix}

Így az (1), (2) és (3) egy egyenletrendszert alkot, amelyben

V_{1}

V_{2}

és

T_{2}

az ismeretlenek. Ennek megoldását egy konkrét példán, éppen a hidrogén esetében végezzük el.
Vegyünk

1

molnyi, azaz

2

gramm hidrogént, amelynek nyomása

p_{1} = 100

atm, hőmérséklete

T_{1} = 0 C^{\circ} = 273, 16 K^{\circ}

. Az előbb vázolt eszközben terjesszük ezt ki

1

atm-ra. Kérdés, hogy mennyi lesz ekkor a hőmérséklet ?
Először a (2) egyenletből meghatározzuk

V_{1}

-et (ill. elegendő meghatározni

p_{1} V_{1}

-et). Beszorozva és átrendezve:

\begin{matrix} p_{1} V_{1} = R T_{1} - \frac{a}{V_{1}} + b p_{1} + \frac{a b}{V_{1}^{2}} . \end{matrix}

Mivel így harmadfokú egyenletet kapnánk, ezért egyszerűség kedvéért a korrekciós tagokban egy kis elhanyagolást végzünk. Feltehetően nem jelent lényeges eltérést, ha a jobboldalon levő

V_{1}

-ek helyébe az ideális gáztörvény alapján kapott

\frac{R T_{1}}{p_{1}}

értéket helyettesítjük, ebből:

\begin{matrix} p_{1} V_{1} = R T_{1} - \frac{a p_{1}}{R T_{1}} + p_{1} b + \frac{a b p_{1}^{2}}{R^{2} T_{1}^{2}} = 23, 62 atm  lit/mol. \\ (1) alapján, mivel p_{2} = 1 atm: V_{2} = p_{1} V_{1} / p_{2} = 23, 62 lit/mol. \end{matrix}

Ezt behelyettesítve (3)-ba:

T_{2} = \frac{(p_{2} + \frac{a}{V_{2}^{2}}) \cdot (V_{2} - b)}{R} = 287, 73 K^{\circ}

,
tehát a hőmérséklet-növekedés:

Δ T = 14, 57 K^{\circ}

.
Ugyanezt a kísérletet nitrogénnel elvégezve:

V_{2} = \frac{p_{1} V_{1}}{p_{2}} = 21, 31

lit, és

T_{2} = 260, 00 K^{\circ}

, tehát a hőmérséklet-növekedés:

Δ T = - 13, 16 K^{\circ}

(tehát hőmérséklet-csökkenés van). Ebből látható, hogy a hidrogén felmelegedése nem a véletlen műve, hanem a hidrogén tulajdonságaiból törvényszerűen következik. Nehogy azt gondoljuk azonban, hogy ez a felmelegedés a hidrogén egyedüli sajátsága, ugyanis bizonyos nyomáshatárok között minden gáz felmelegszik a kiterjesztés hatására. Ennek bizonyítására vizsgáljuk meg részletesebben a következő képletet:

\begin{matrix} Δ T = T_{2} - T_{1} = \frac{\frac{2 a}{R T_{1}} - b - \frac{3 a b p_{1}}{R^{2} T_{1}^{2}}}{c_{p}} (p_{2} - p_{1}) . \end{matrix}

Ez az itt nem részletezhető úton levezetett összefüggés explicite megadja minden gázra a kis

Δ p = p_{2} - p_{1}

nyomásváltozás hatására bekövetkező hőmérséklet-változást.
A továbbiakban egyszerűség kedvéért ennek a

Δ T

-nek csak az előjelét fogjuk vizsgálni. Mivel

c_{p}

, az állandó nyomáson vett fajhő pozitív és

Δ p

negatív (mivel

p_{2} < p_{1}

), ezért csak a

μ = \frac{2 a}{R T_{1}} - b - \frac{3 a b p_{1}}{R^{2} T_{1}^{2}}

kifejezés érdekel bennünket. Ha ide behelyettesítjük a hidrogén előző kísérletbeli adatait, akkor negatív értéket kapunk (tehát

Δ T > 0

), ha pedig a nitrogén adatait helyettesítjük be, akkor pozitívat (tehát

Δ T < 0

).
De ha az előző kísérletben a nitrogént nem

100

atm-ra, hanem mondjuk

500

atm-ra nyomjuk össze, és csak aztán terjesztjük ki, akkor ‐ mivel a

μ = \frac{2 \cdot 1, 345}{R \cdot 273} - 0, 0385 - \frac{3 \cdot 1, 345 \cdot 0, 0385 \cdot 500}{R^{2} \cdot 273}

kifejezés értéke körülbelül

- 0, 07

, vagyis negatív, ezért a nitrogén is felmelegszik (persze a kiterjesztés itt nem mehet

1

atm-ig, mert a fenti képlet csak kis

p_{1} - p_{2}

esetén érvényes).
Viszont ha van olyan nyomás, amelyen kis kiterjedés esetén felmelegedés, ill. lehűlés következik be, akkor a kettő között kell lennie egy olyan nyomás-értéknek, ahol ez az előjelváltozás megtörténik. Ekkor

μ = 0

, ebből:

\begin{matrix} \frac{2 a}{R T} - b - \frac{3 a b p}{R^{2} T^{2}} = 0. \end{matrix}

Nitrogén esetén

0 C^{\circ}

-on

p = 250

atm.

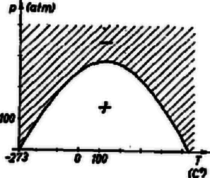2. ábra

Ha más

T

hőmérsékleten vizsgáljuk a jelenséget, akkor természetesen más

p

értéket kapunk. Ha ezeket az összetartozó

p - T

értékeket koordináta rendszerben ábrázoljuk, akkor parabolát kapunk. Ugyanis

- \frac{T^{2}}{b}

-vel beszorozva a

T^{2} - \frac{2 a}{R b} T +

+ \frac{3 a p}{R^{2}} = 0

valóban egy parabola egyenlete, melynek görbéjét nitrogén esetén a 2. ábra mutatja.
A megfelelő

(p; T)

értékpárokat inverziós pontoknak nevezzük, az általuk meghatározott görbét pedig inverziós görbének. Ennek a görbének az a tulajdonsága, hogy az alatta levő

(p; T)

pontokra

μ

pozitív, vagyis az ilyen állapotú gáz esetén a nyomás-csökkenés mindig hőfok-csökkenéssel jár. A felette levő

(p; T)

pontokra pedig mindaddig a hőmérséklet emelkedésével jár, amíg olyan kicsi nyomáshoz nem érünk, hogy a

(p; T)

pont a görbe alá kerül.
Mivel a reális gázoknak az ideális gáztól való ilyen eltéréseit szabatosan elsőként Joule és Thomson vizsgálták klasszikus kísérleteikben, ezért ezt a jelenséget Joule‐Thomson-effektusnak nevezik.
Láthatjuk tehát, hogy a Van der Waals állapotegyenletből tisztán matematikai úton levezethető a gázok kiterjesztéskor fellépő hőfokváltozása, sőt annak nagyságára is jó közelítéssel szolgál.
Arra a problémára azonban, hogy a hidrogén esetén honnan keletkezik, a nitrogén esetén hová tűnik a hőenergia, ez az egyenlet sem ad választ. Erre a kérdésre a magyarázatot mélyebben, a molekulák közti kölcsönhatás részletesebb vizsgálatában kell keresnünk.
Ha a gáz nyomását változtatjuk, akkor megváltozik a térfogat-egységben levő molekulák száma, s így ezen molekulák átlagos távolsága. A továbbiakban éppen ez a távolság fog nagy szerepet játszani.
Egyszerűség kedvéért egyelőre csak két molekula állapotát vizsgáljuk egymástól mért távolságuk függvényében.
E két molekula között különböző okokból vonzó

(P_{1})

és taszító erő

(P_{2})

lép fel, amelyek fordítottan arányosak a köztük levő távolság bizonyos (

κ_{1}

és

κ_{2}

) hatványával, így a következő alakban írhatjuk őket:

\begin{matrix} P_{1} = \frac{c_{1}}{r^{κ_{1}}}, P_{2} = \frac{c_{2}}{r^{κ_{2}}} \end{matrix}

ahol

c_{1}

és

c_{2}

jellemző anyagi állandók.
Hogy

P_{1}

vonzóerő, azt a negatív előjellel jelezzük. Pillanatnyilag tételezzük fel, hogy taszítóerő nem hat, ekkor ‐ ha el akarjuk egymástól távolítani a molekulákat, a vonzóerő ellen munkát kell végeznünk. Azt a munkát, amelyet akkor végzünk, amikor az egyik molekulát az adott

r

távolságból a végtelenbe visszük, a molekula helyzeti (potenciális) energiájának nevezzük. Ennek az

r

-től való függését a következő függvény írja le:

E'_{p o t} = - \frac{c'}{r^{k_{1}}}

, ahol

k_{1} = κ_{1} - 1 \approx 6

, és

c'

állandó. (Azért negatív, mert az eltávolításhoz valahonnan máshonnan kell az energiát elvonni.) A görbe menetét a grafikon mutatja.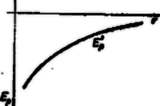

3. ábra

Ha pedig csak a taszítást vesszük figyelembe, akkor az erőtér végez munkát, miközben a molekulák távolodnak. Az az energia-mennyiség, amely a végtelenbe távolodáskor felszabadul, szintén a két molekula adott pontbeli potenciális energiáját jelenti, és nagysága

E''_{p o t} = - \frac{c''}{r^{k_{2}}}

, ahol

k_{2} = κ_{2} - 1 \approx 12

, és

c''

konstans.

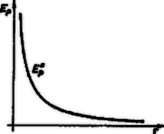4. ábra

Mivel a valóságban a vonzás és taszítás mindig együttesen hat, ezért az eredő potenciális energia az előző kettő algebrai összegével lesz egyenlő:

E_{p} = - \frac{c'}{r^{k_{1}}} + \frac{c''}{r^{k_{2}}}

E_{p}

-t megkapjuk a molekulák távolságának függvényében, ha az előző két diagramot grafikusan összegezzük.
Mivel

k_{1} < k_{2}

, azért nagyon kicsi

r

esetén:

a = \frac{E''_{p}}{E'_{p}} = - \frac{c''}{r^{k_{1}}} \cdot \frac{r^{k_{1}}}{c'} = \frac{c''}{c'} \cdot \frac{1}{r^{k_{2} - k_{1}}}

, ahol

- \frac{c''}{c'}

konstans, és

r^{k_{2} - k_{1}}

nagyon kicsi lévén

a

nagyon nagy lehet, vagyis

E''_{p}

abszolut értéke mellett

E'_{p}

elhanyagolható.

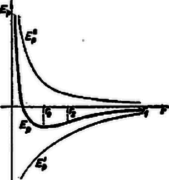5. ábra

Nagy

r

esetén azonban éppen fordítva áll a dolog, mert

r^{k_{2} - k_{1}}

nagyon nagy lehet. Ez összegezve azt jelenti, hogy

E_{p}

függvény kis

r

esetén azonosnak tekinthető

E''_{p}

-vel, vagyis ezen a szakaszon a vonzóerők elhanyagolhatók. Nagy

r

esetén pedig az

E'_{p}

-vel azonos, vagyis itt a taszítóerők hanyagolhatók el. Az átmeneti szakaszon a görbe minimumon megy át, mert előtte monoton fogyó, utána pedig növekedő.
Ezen előzetes megjegyzések után térjünk újra vissza a gázok kiterjesztésére, ill. összenyomására. A kiindulási állapotban olyan legyen a nyomás, hogy a molekulák távolsága a grafikonon jelzett viszonylag nagy

r_{1}

érték legyen. Nyomjuk össze a gázt annyira, hogy ez a távolság

r_{2}

legyen. Láthatjuk, hogy itt a molekulák kölcsönös helyzeti energiája csökkent, vagyis energia szabadult fel. Feltételezve, hogy a gáz zárt rendszert alkot, mivel ez az energia nem távozhat el, azért csak a molekulák mozgási energiájának a növelésére fordítódhat. De ez azt jelenti, hogy a gáz hőmérséklete növekszik, ugyanis a testek hőmérsékletét csak a molekulák közepes mozgási energiája,

\bar{ω_{0}}

szabja meg: definíciószerűen

T = \frac{2}{κ} \bar{ω_{0}}

. Vagyis

\bar{ω_{0}}

növekedése maga után vonja

T

-ét is. (

k

a Boltzmann-állandó, értéke

1, 3805 \cdot 10^{- 16}

erg/fok.)
A nyomás növelésével mindaddig nő a hőmérséklet, amíg az átlagos távolság egy bizonyos

r_{0}

-nál nagyobb, addig a pontig ugyanis a helyzeti energia csökken. Ezután azonban már helyzeti energianövekedés következik, amely hasonló okokból, mint előbb, most éppen a hőmérséklet csökkenésével jár.
Tehát ha bármilyen összetételű gázból indulunk ki, bár kezdetben az összenyomás hatására nőhet a hőmérséklet (amíg viszonylag nagy a molekulák átlagos távolsága), de egy bizonyos ponton a hőmérséklet-változás okvetlenül előjelet vált. Az ehhez az állapothoz tartozó

(p; T)

értékpár éppen a Van der Waals egyenletből levezetett inverziós ponttal azonos. Vegyük észre, hogy ha különböző kezdeti állapotokból indulunk ki (más a rendszer összes belső energiája), akkor a megfelelő

(p; T)

párok is különbözők lesznek.
Kiterjesztéskor persze éppen ellentétes folyamat játszódik le. Vagyis elég nagy nyomáson kiterjesztés hatására minden gáz felmelegszik. Hidrogén esetén már az

1

atm, nitrogénnél pedig csak több száz atm jelent ilyen elég nagy nyomást.
Végül megállapíthatjuk, hogy a folyamat molekuláris vizsgálata teljesen megszünteti az energetikai szempontból felmerült aggályainkat. Ugyanis az energia-megmaradás elvével megegyezésben itt sem történik egyéb, mint az energia egyik formájából (molekulák mozgási energiája) a másikba (kölcsönös helyzeti energia) történő átalakulása.

Vesztergombi György