Kezdőlap


Cím:	A görbületi sugárról
Szerző(k):	Vermes Miklós
Füzet:	1964/március, 129 - 133. oldal	PDF \| MathML
Témakör(ök):	Szakmai cikkek

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Néhány olyan kérdésről lesz szó, amely a görbületi kör és a görbületi sugár szerepét mutatja be, egyszersmind megismerkedünk ezekkel a fogalmakkal. Kiindulásul választjuk a homorú tükör képalkotását. Ismeretes, hogy az $r$ rádiuszú homorú gömbtükör $t$ távolságban levő tárgyakról $k$ távolságban ad képet és a tengely közelében haladó sugarak esetében jó közelítésben érvényes ez a törvény:

\begin{matrix} \frac{1}{t} + \frac{1}{k} = \frac{2}{r} = \frac{1}{f} . \end{matrix}

(1)

f = r / 2

neve fókusztávolság. A tengellyel párhuzamosan beeső sugarak a fókuszpontban találkoznak visszaverődés után, a fókuszpont tükörtől mért távolsága a fókusztávolság.

t

és

k

is a tükörtől számítandók.
Most az ellipszoid tükör viselkedését fogjuk tanulmányozni. Homorú tükrünk egy forgási ellipszoid, ennek metszetét tünteti fel az 1. ábra. Ellipszisünk fókuszai

F_{1}

és

F_{2}

, fél nagytengelye

A C = C B = a

, fél kistengelye

D C = C E = b

, excentritása

F_{1} C = C F_{2} = c

. Ismeretes, hogy

a^{2} = b^{2} + c^{2}

. Az

X

ponthoz tartozó vezérsugarak

r_{1} = F_{1} X

r_{2} = F_{2} X

. Az ellipszis definíciója szerint bármely pontban

r_{1} + r_{2} = 2 a .

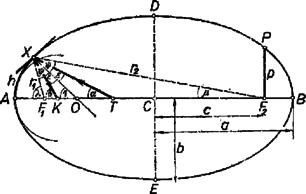1. ábra

Ellipszis alakú tükrünk

A

csúcspont körüli részét használjuk, és az ellipszis nagytengelyén helyezzük el

T

-ben a fényforrást. A belőle kiinduló egyik fénysugár

α

szöget zár be a tengellyel és

X

-ben éri el a tükröt. A beesési merőleges szerepét most

r_{1}

és

r_{2}

vezérsugarak szögfelezője

(X O)

tölti be mint a tükör érintkezőjének merőlegese, és ez az egyenes mindegyik vezérsugárral

ψ

szöget alkot. Az

ε

beesési szöggel érkező fénysugár ugyanakkora szöggel verődik vissza, majd

K

-ban metszi a tengelyt,

β

szögben. A vezérsugarak szögfelezője

γ

szögben metszi a tengelyt.

\begin{matrix} Az O T X_{4} -ből : ε + α = γ, \\ a K O X_{4} -ből : β = γ + ε, \end{matrix}

összegezve:

α + β = 2 γ

.
Tehát

γ

szög

α

és

β

számtani középértéke. Az

O F_{2} X_{4}

és

F_{1} O X_{4}

elhelyezkedéséből látszik, hogy

γ

a vezérsugarak

λ

és

μ

szögének is számtani középértéke:

\begin{matrix} 2 γ = λ + μ, \end{matrix}

ezért:

α + β = λ + μ

.
Ez minden közelítés nélkül pontosan igaz.
Ezután a szögek helyett távolságokat hozunk be, de ekkor olyan közelítéseket kell használnunk, amelyek csak a tengely közelében haladó fénysugarak esetében engedhetők meg. Először is a szögek helyébe a tangenseiket írjuk:

\begin{matrix} tgα+ tgβ= tgλ+ tgμ, \end{matrix}

azután beírjuk ezek közelítő értékeit az 1. ábra alapján:

\begin{matrix} \frac{h}{A T} + \frac{h}{A K} = \frac{h}{A F_{1}} + \frac{h}{A F_{2}} . \end{matrix}

h

kiegyszerűsíthető, ami azt jelenti, hogy képalkotás van, vagyis minden

T

-ből kiinduló fénysugár ugyanazon

K

pontban találkozik (a közelítéseket figyelembe véve). Az

A T = t

távolságot tárgytávolságnak, az

A K = k

távolságot képtávolságnak nevezzük. Továbbá

A F_{1} = a - c

A F_{2} = a + c

, tehát

\begin{matrix} \frac{1}{t} + \frac{1}{k} = \frac{1}{a - c} + \frac{1}{a + c} = \frac{a + c + a - c}{a^{2} - c^{2}} = \frac{2 a}{b^{2}} . \end{matrix}

Tehát a tárgytávolság és képtávolság reciprok értékeinek összege állandó. Ebben az állandóban

\begin{matrix} ϱ = \frac{b^{2}}{a} \end{matrix}

(2)

ugyanazt a szerepet tölti be, mint a gömbtükör (1) alatti törvényében a gömb

r

rádiusza. Ha ezzel a

ϱ

rádiusszal készítünk el egy gömbtükröt, és ellipszis tükrünk helyére tesszük, akkor a képalkotásban semmi különbséget sem találunk.

ϱ

-tól eltérő rádiuszú gömbök esetében

T

tárgy képe

K

-nál közelebb vagy távolabb keletkezne. Valamennyi létező kör közül ez a

ϱ

rádiuszú kör simul legjobban az ellipszishez az

A

csúcspontban, és képalkotás szempontjából az ellipszistükör

ϱ

rádiuszú gömbtükörrel pótolható. A (2) szerinti

ϱ

rádiusz neve az

A

ponthoz tartozó görbületi sugár, és a vele rajzolt kör (az 1. ábrán szaggatott vonal) a görbületi kör.
Az ellipszis függvényéből következik, hogy

ϱ

egyenlő a fókuszpontban emelt

p = F_{2} P

ordinátával, az ellipszis úgynevezett paraméterével. Hasonló számítást végezhettünk volna el a hiperbolára vonatkozóan is. Számításunk tartalmazza a gömbtükör távolság törvényének levezetését is, mert kör esetében

a = b = r

és

ϱ = r

.
Eddigi gondolatmenetünk az ellipszis csúcspontjára vonatkozott, de meg kell vizsgálnunk az ellipszis egyéb pontjait is, vagyis meg kell keresnünk a görbületi sugár nagyságát az ellipszis tetszés szerinti pontjához tartozóan. Kissé hosszabb számítás vár ránk, de az eredmény érdekes lesz. 2. ábránk ellipszis alakú tükrének

Y

pontját vizsgáljuk és optikai tengelyünk az

Y

-ban rajzolt érintő merőlegese, az

F_{1} Y F_{2}

szög szögfelezője. Az

Y O

optikai tengely mindegyik vezérsugárral

ψ

szöget alkot. A tengellyel párhuzamosan érkező fénysugár

X

-ben verődik vissza a tükörről, miközben

X O

szögfelező a beesési merőleges, amelynek két oldalán találjuk

γ

beesési és visszaverődési szögeket. Ugyanez a

γ

adja meg az

X O

szögfelezőnek a tengellyel alkotott

X O Y ∢ = γ

szögét is. Azonnal látszik, hogy

β = 2 γ

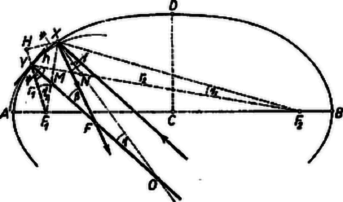2. ábra

Az ellipszis

Y X

íve

F_{1}

fókuszból

γ_{1}

F_{2}

fókuszból

γ_{2}

szög alatt látszik. Az

F_{1} M Y

és

O M X

háromszögekből, mert

M

-nél csúcsszög van:

\begin{matrix} γ_{1} + ψ = γ + F_{1} X O ∢, \end{matrix}

hasonlóan az

F_{2} N X

és

O N Y

háromszögekből, az

N

-nél levő csúcsszög folytán:

\begin{matrix} γ_{2} + F_{2} X O ∢ = γ + ψ . \end{matrix}

Az egyenleteket összeadva, és mivel

X O

F_{1} X F_{2}

szög felezője:

\begin{matrix} γ_{1} + γ_{2} = 2 γ . \end{matrix}

Érdekes, hogy

γ_{1}

és

γ_{2}

szögek számtani középértéke

γ

. Ez minden közelítés nélkül igaz. Ezzel

β

-ra vonatkozó összefüggésünk:

\begin{matrix} β = γ_{1} + γ_{2} . \end{matrix}

Most vesszük figyelembe, hogy

Y X = h

ív igen kicsiny és ennek értelmében közelítünk.

H X

merőleges

r_{1}

-re, ezért

H X = h cos ψ

. Radiánban kifejezve

γ_{1} = H X / r_{1} = h cos ψ / r_{1}

. Ugyanígy

γ_{2} = h cos ψ / r_{2}

. Radiánban kifejezve

β = h / Y F

. Ezeket felhasználva:

\begin{matrix} \frac{h}{Y F} = \frac{h cos ψ}{r_{1}} + \frac{h cos ψ}{r_{2}} . \end{matrix}

h

kiesése azt bizonyítja, hogy a közelítések érvényessége mellett a párhuzamosan beeső sugarak

F

fókuszban találkoznak. A fókusztávolság:

\begin{matrix} Y F = f = \frac{r_{1} r_{2}}{(r_{1} + r_{2}) cos ψ} = \frac{r_{1} r_{2}}{2 a cos ψ} . \end{matrix}

Még egy lépés szükséges a vezérsugarak kifejezésére. Felírjuk

F_{1} Y F_{2}

háromszögre a cosinus tételt:

\begin{matrix} {(2 c)}^{2} & = r_{1}^{2} + r_{2}^{2} - 2 r_{1} r_{2} cos 2 ψ = r_{1}^{2} + r_{2}^{2} - 2 r_{1} r_{2} (2 cos^{2} ψ - 1) = \\ = r_{1}^{2} + 2 r_{1} r_{2} + r_{2}^{2} - 4 r_{1} r_{2} cos^{2} ψ = \\ = {(r_{1} + r_{2})}^{2} - 4 r_{1} r_{2} cos^{2} ψ = {(2 a)}^{2} - 4 r_{1} r_{2} cos ψ, \end{matrix}

innen a vezérsugarak szorzata:

\begin{matrix} r_{1} r_{2} = \frac{a^{2} - c^{2}}{cos^{2} ψ} = \frac{b^{2}}{cos^{2} ψ} . \end{matrix}

Ezt felhasználva a fókusztávolság

b^{2} / 2 a cos^{3} ψ

, és a fókusztávolság kétszerese, a görbületi sugár:

\begin{matrix} ϱ = \frac{b^{2}}{a cos^{3} ψ} . \end{matrix}

(3)

Ez az igen érdekes képlet adja meg általánosságban a görbületi sugarat az ellipszis tetszés szerinti pontjában. Az ekkora rádiuszú kör (a 2. ábrán a szaggatott vonal) simul legjobban az ellipszishez, ilyen rádiuszú gömbtükörrel helyettesíthetjük az ellipszis tükröt. Érdekes, hogy az ellipszis keresztülhalad a görbületi körön, mert

Y

-tól

A

felé görbültebb,

Y

-tól

D

felé kevésbé görbült, mint a görbületi kör.
(3) képletünkben

ψ

, a vezérsugarak szögének fele a független változó. Az ellipszis

A

csúcsában

ψ = 0

cos ψ = 1

és

ϱ = b^{2} / a

, megegyezésben (2)-vel, ekkor

ϱ

-nak minimuma van, itt az ellipszis a leggörbültebb. Az ellipszis

D

csúcsában

cos ψ = b / a

, és

ϱ = a^{2} / b

; most

ϱ

-nak maximuma van, itt az ellipszis a legkevésbé görbült. Különben

ϱ

felírható a paraméterrel is:

ϱ = p / cos^{3} ψ

.
Nemcsak a fénytanban, hanem a mechanikában is nagy szerepe van a görbületi körnek. Ismeretes, hogy

m

tömegű test

r

rádiuszú körpályán

ω

szögsebességgel,

v

tényleges sebességgel végbemenő körmozgásához

P = m ω^{2} r = m v^{2} / r

centripetális erő szükséges. De mi van nem körön végbemenő görbevonalú mozgás esetében ? A bolygómozgás példáján adunk erre választ.
Bolygónk ebben a pillanatban az

F

-ben álló igen nagy

M

tömegű Naptól

R F = r

távolságban halad

v

sebességgel; a sebesség merőlegese

ψ

szöget alkot

r

összekötő egyenessel (3. ábra). Ha a bolygó

m

tömege elhanyagolható a Nap tömege mellett, akkor a Nap nyugalomban levőnek tekinthető. Newton felfedezése szerint a bolygó és a Nap között

f m M / r^{2}

nagyságú kölcsönös vonzóerő működik az összekötő egyenes mentén (

f

a gravitációs állandó). Ennek hatására a bolygó valamilyen görbe pályán mozog, még nem tudjuk, milyenen.

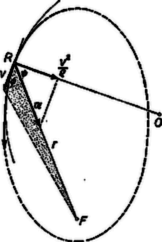3. ábra

Először használjuk fel a tömegvonzási erő azon tulajdonságát, hogy centrális erő, vagyis a tömegek összekötő egyenesében hat. Ebből következik függetlenül az erőtörvény és a pálya alakjától, hogy a területi sebesség állandó. A vezérsugár által

1

másodperc alatt leírt terület:

\begin{matrix} \frac{v r cos ψ}{2} = K . \end{matrix}

(4)

Ez a mennyiség állandó egy magára hagyott bolygó esetében. A törvény bizonyítása megtalálható a Középiskolai Matematikai Lapok XIX. Kötet, 1959. nov.-i számában a 154. oldalon. Az összekötő egyenes mentén működő erő következménye az is, hogy a pálya

v

-n és

F

-en átmenő síkban fekszik.
Csak most használjuk fel az erőtörvény négyzetes sajátosságát. A bolygó

a = f M / r^{2}

teljes gyorsulása

F

felé irányul, és van az érintőre merőleges összetevője:

\begin{matrix} a cos ψ = \frac{f M cos ψ}{r^{2}} . \end{matrix}

A gyorsulás ezen összetevőjét kell egyenlővé tenni a centripetális gyorsulással. Ennek kiszámítását úgy végezzük, hogy az ismeretlen alakú görbe pályát

R

pontban

R O = ϱ

sugarú görbületi körével helyettesítjük, tehát a centripetális gyorsulás

v^{2} / ϱ

. Egyenlővé téve a teljes gyorsulás merőleges összetevőjével:

\begin{matrix} \frac{f M cos ψ}{r^{2}} = \frac{v^{2}}{ϱ} . \end{matrix}

Innen a görbületi sugár:

ϱ = \frac{v^{2} r^{2}}{f M cos ψ}

.
Ide behelyettesítjük (4) alapján

v r

értékét:

\begin{matrix} ϱ = \frac{\frac{4 K^{2}}{f M}}{cos^{3} ψ} . \end{matrix}

(5)

A számláló állandó és a nevezőben az irányt meghatározó szög cosinusának köbe szerepel! Óriási eredmény: ez az ellipszis görbületi sugara. Ezzel bebizonyítottuk, hogy a tömegvonzási törvény alapján létrejövő bolygópályák ellipszisek (kúpszeletek), amelyek egyik fókuszában a Nap áll.
Számításunk eredménye Kepler I. törvénye. Kepler II. törvényét a területi sebesség tétele tartalmazta. Hátra van még Kepler III. törvényének bizonyítása. (5) alatti eredményünkben

4 K^{2} / f M = p = b^{2} / a

az ellipszis paramétere. Ebből a területi sebesség:

\begin{matrix} K = \frac{b}{2} \sqrt[]{\frac{f M}{a}} . \end{matrix}

Minthogy az ellipszis területe

π a b

, ha a bolygó keringési ideje

T

, akkor a területi sebesség:

K = \frac{π a b}{T}

.
Egyenlővé téve:

\begin{matrix} \frac{b}{2} \sqrt[]{\frac{f M}{a}} = \frac{π a b}{T}, \end{matrix}

innen a keringési idő négyzete:

\begin{matrix} T^{2} = \frac{4 π^{2}}{f M} \cdot a^{3} . \end{matrix}

Ez Kepler III. törvénye, amely szerint a keringési idő négyzete arányos a fél nagytengely köbével. Igen nevezetes, hogy a kistengely hossza nem szerepel, ettől független a keringési idő. A bolygómozgás egyéb kérdéseire is választ kaphatunk képleteinkből.

Vermes Miklós