Cím:	1963. évi Eötvös Loránd Fizikaverseny
Füzet:	1964/február, 81 - 84. oldal	PDF  |  MathML
Témakör(ök):	Eötvös Loránd (korábban Károly Irén)

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. Az 1963. évi Eötvös Loránd fizikai verseny   Az Eötvös Loránd Fizikai Társulat október 19-én rendezte ez évi Eötvös Loránd fizikai versenyét Budapesten és 6 vidéki városban az idén érettségizettek számára. A versenyzők 5 óráig dolgozhattak és bármilyen segédeszközt használhattak. Az alábbiakban ismertetjük a verseny feladatait és azok megoldását.   1. $2$ méter hosszú, $8$ centiméter átmérőjű vízszintes rúd közepén és egyik végén csapágyazva van. A csapágyak csúszó súrlódási együtthatója $0\mathrm{,}05$. A rúd másik végén $10$ centiméter átmérőjű tárcsa van, amelynek kerületéről fonál lóg le. Mekkora súly akasztható e fonál végére, hogy a rúd (a súrlódás folytán) még ne jöjjön forgásba? A rúd és tárcsa önsúlya elhanyagolandó. 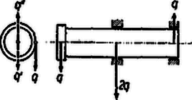    1. ábra   Megoldás. A fonálra akasztott $q$ súly a tárcsa kerületéről lecsüngő fonálon lóg (1. ábra). A tárcsa középpontjában hozzáveszünk függőlegesen felfelé irányuló, ugyanakkora $q\text{'}$ és $q\text{'}\text{'}$ erőket. Közülük $q\text{'}$ a rúd tárcsás végét le akarja hajlítani. Ezt a $q\text{'}$ erőt a csapágyakban függőlegesen lefelé ható $2q$ és függőlegesen felfelé ható $q$ erők ellensúlyozzák. $q$ és $q\text{'}\text{'}$ erőkből álló erőpár $5q$ forgatónyomatékkal forgatja a rudat. $\mu$ súrlódási együttható esetében $2\mu q$ és $\mu q$ a lehetséges legnagyobb súrlódási erők, tehát az a legnagyobb forgatónyomaték, amely a súrlódási erő által létre jöhet: $\begin{array}{c}{\displaystyle 2\mu q\cdot 4+\mu q\cdot 4=12\mu q\mathrm{.}}\end{array}$ A súrlódási erő szempontjából nem lényeges, hogy a $2q$ és $q$ erők felfelé vagy lefelé hatnak-e, mindenképp ugyanaz a súrlódási erő szerepel, ha az erő merőlegesen szorítja egymáshoz a csúszó felületeket. A szerkezet nyugalomban maradásának az a feltétele, hogy a lehetséges legnagyobb súrlódási forgatónyomaték egyenlő vagy nagyobb legyen, mint a fonálra akasztott súly forgatónyomatéka: $\begin{array}{c}{\displaystyle 5q\le 12\mu q\mathrm{,}\text{adatainkkal:}5q\le 0\mathrm{,}6q\mathrm{.}}\end{array}$ Látható, hogy ez a feltétel csak $q=0$ esetében teljesülhet, ami azt jelenti, hogy a szerkezet már a fonálra akasztott legkisebb terhelés mellett is forgásba jönne. Érthető az ok: $q$ növelése ugyanolyan mértékben növeli a rudat forgató forgatónyomatékot, mint a súrlódási erők forgatónyomatékát.   Egyensúlyfeltételünkből látható, hogy $\mu =5/12=0\mathrm{,}416$ vagy ennél nagyobb súrlódási együttható esetében a rúd nem jönne forgásba bármilyen nagy ráakasztott teher esetében sem. Ugyanígy elérhető a nyugalom feltétele a rádiuszok megfelelő változtatásával is.   Más a helyzet, ha figyelembe vesszük a rúd önsúlyát ($Q$). Ha az egész szerkezet súlypontja nincs a csapágyakon kívül, akkor az önsúly folytán létrejövő súrlódási erő $\mu Q$, és ennek forgatónyomatéka $4\mu Q$. Ezt hozzáadjuk egyensúlyfeltételünk jobb oldalához ($0\mathrm{,}05$ értékű súrlódási együtthatóval): $5q\le 0\mathrm{,}6q+0\mathrm{,}2Q$. Most nem egyszerűsíthetünk $q$-val és megállapíthatjuk az egyensúly feltételét. Feladataink számadatai mellett az egyensúly feltétele: $q\le Q/22$.   2. Hogyan méretezendő a rajz szerinti kapcsolásban a kondenzátor és az önindukciós tekercs, hogy adott rezgésszámú és nagyságú váltófeszültség mellett az izzólámpák ugyanakkora áramerősséggel égjenek, tekintet nélkül arra, hogy hány darab egyforma izzólámpát használnak?   Megoldás. Ha a berendezés $A$ és $C$ pontjára szinuszos váltófeszültséget kapcsolunk, akkor bármely két pont között fellépő váltófeszültség és bármely alkatrészben folyó áramerősség ugyanolyan rezgésszámú színuszfüggvény szerint változik, de az amplitúdók és fázisok a legkülönbözőbbek lehetnek (2. ábra). Feltételezzük, hogy az együttesen $r$ ellenállású izzólámpa-sorozatban $i_r=i_{r0}\text{sin}\omega t$ váltóáram van, és ebből állapítjuk meg, miféle váltófeszültségnek kell $A$ és $C$ között lennie. $\omega$ körfrekvencia mindvégig adott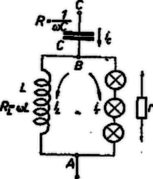, $t$ az idő.     2. ábra   Ohm törvénye szerint az ohmos ellenálláson, vagyis $A$ és $B$ között jelen levő váltófeszültség $U_{AB}=r{i}_{r0}\text{sin}\omega t$. Ugyanez a váltófeszültség van az $L$ önindukciójú, $R_L=\omega L$ induktív ellenállású tekercs végein is. A tekercs árama ${90}^{\circ }$-kal késik a feszültséghez képest: $\begin{array}{c}{\displaystyle i_L=\frac{r}{RL}\cdot i_{r0}\text{sin}\left(\omega t-{90}^{\circ }\right)\mathrm{.}}\end{array}$ Összegeznünk kell a párhuzamosan kapcsolt ohmos ellenállás és a tekercs áramerősségét. Mindegyik ugyanolyan hullámhosszú szinuszfüggvény, de eltérő amplitúdóval és fázissal.   Két eltérő amplitúdójú és fázisú sinus összegezésének általános eljárása a következő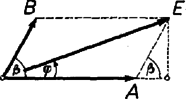: ${\displaystyle \begin{array}{c}\hfill {\displaystyle A\text{sin}\omega t+B\text{sin}\left(\omega t+\beta \right)=A\text{sin}\omega t+B\text{cos}\beta \text{sin}\omega t+}\hfill \\ \hfill {\displaystyle +B\text{sin}\beta \text{cos}\omega t=\left(A+B\text{cos}\beta \right)\text{sin}\omega t+B\text{sin}\beta \text{cos}\omega t=}\hfill \\ \hfill {\displaystyle =E\left[\frac{A+B\text{cos}\beta }{E}\cdot \text{sin}\omega t+\frac{B\text{sin}\beta }{E}\cdot \text{cos}\omega t\right]\mathrm{,}}\hfill \end{array}}$ ahol $\begin{array}{c}{\displaystyle E=\sqrt[]{{\left(A+B\text{cos}\beta \right)}^2+{\left(B\text{sin}\beta \right)}^2}\mathrm{.}}\end{array}$ Ez az azonos átalakítás lehetővé teszi, hogy a $\text{sin}\omega t$ és $\text{cos}\omega t$ előtt álló szorzókat ugyanazon szög $\text{cos}$-ának és $\text{sin}$-ának tekintsük, mert e mennyiségek négyzetösszege 1. Ugyanezen $\phi$ szög tangense: $\begin{array}{c}{\displaystyle \text{tg}\phi =\frac{B\text{sin}\beta }{A+B\text{cos}\beta }\mathrm{.}}\end{array}$ Tehát két színuszhullámunk összege: $\begin{array}{c}{\displaystyle E\left[\text{cos}\phi \text{sin}\omega t+\text{sin}\phi \text{cos}\omega t\right]=E\text{sin}\left(\omega t+\phi \right)\mathrm{.}}\end{array}$     3. ábra   3. ábránk mutatja, hogy $E$ olyan paralelogrammának átlója, melynek oldalai $A$ és $B$, az oldalak szöge $\beta$, és $E$-nek $A$-val alkotott szöge $\phi$. Számításunk ezen geometriai értelmezése teszi lehetővé színuszhullámok grafikus összegezését az ún. vektordiagramokkal.   Összegezzük az ohmos ellenálláson és a tekercsen átfolyó áramokat: $\begin{array}{c}{\displaystyle i_r+i_L=i_{r0}\text{sin}\omega t+\frac{r}{R_L}\cdot i_{r0}\text{sin}\left(\omega t-{90}^{\circ }\right)=i_{r0}\sqrt[]{1+{\left(r/R_L\right)}^2}\cdot \text{sin}\left(\omega t-\phi \right)\mathrm{,}}\end{array}$ ahol $\begin{array}{c}{\displaystyle \text{tg}\phi =\frac{r}{R_L}\mathrm{,}\text{sin}\phi =\frac{r/R_L}{\sqrt[]{1+{r/R_L}^2}}\text{cos}\phi =\frac{1}{\sqrt[]{1+{\left(r/R_L\right)}^2}}\mathrm{.}}\end{array}$ Ez lesz a kondenzátor árama: $i_r+i_L=i_C$. A kondenzátor feszültségkülönbsége ehhez képest késik ${90}^{\circ }$-kal: $\begin{array}{c}{\displaystyle U_{BC}=R_C{i}_C\text{sin}\left(\omega t-\phi -{90}^{\circ }\right)=R_C{i}_{r0}\sqrt[]{1+{\left(r/RL\right)}^2}\cdot \text{sin}\left(\omega t-\phi -{90}^{\circ }\right)\mathrm{.}}\end{array}$ Az egész berendezésre jutó teljes feszültségkülönbség, vagyis az $A$ és $C$ pontok között levő hálózati feszültség: ${\displaystyle \begin{array}{c}\hfill {\displaystyle U=U_{AB}+U_{BC}=r{i}_{r0}\text{sin}\omega t+R_C{i}_{r0}\sqrt[]{1+{\left(r/R_L\right)}^2}\cdot \text{sin}\left(\omega t-\phi -{90}^{\circ }\right)=}\hfill \\ \hfill {\displaystyle =i_{r0}\sqrt[]{r^2+R_C^2\left[1+{\left(r/R_L\right)}^2\right]-2r{R}_C\sqrt[]{1+{\left(r/R_L\right)}^2}\cdot \text{sin}\phi }\cdot \text{sin}\left(\omega t+\gamma \right)=}\hfill \\ \hfill {\displaystyle =i_{r0}\sqrt[]{r^2+R_C^2+r^2{\left(R_C/R_L\right)}^2-2r^2\left(R_C/R_L\right)}\cdot \text{sin}\left(\omega t+\gamma \right)=}\hfill \\ \hfill {\displaystyle =i_{r0}\sqrt[]{R_C^2+r^2{\left(1-R_C/R_L\right)}^2}\cdot \text{sin}\left(\omega t+\gamma \right)\mathrm{.}}\hfill \end{array}}$ Számításunk közben felhasználtuk $\text{sin}\phi$, illetve $\text{cos}\phi$ értékét, és azonos átalakításokat végeztünk. Tehát ha azt akarjuk, hogy az izzólámpa-sorozaton a megkívánt $i_{r0}\text{sin}\omega t$ váltóáram haladjon át, akkor $A$ és $B$ pontokra e képletünk által adott feszültséget kell kapcsolnunk. Ez a feszültség független lesz $r$ ohmos ellenállástól, ha ennek $1-R_C/R_L$ szorzója nullával egyenlő. Ebből következik a feladat megoldása: $\begin{array}{c}{\displaystyle 1-R_C/R_L=\mathrm{0,}{R}_C=R_L\mathrm{,}\frac{1}{{\omega }_C}=\omega L\mathrm{,}\omega =\frac{1}{\sqrt[]{LC}}\mathrm{,}}\end{array}$ tehát a rezonanciaesetet kell beállítanunk. A szinuszok összegezéséből következik, hogy 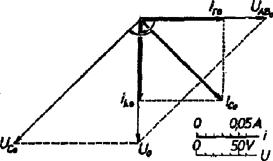$\begin{array}{c}{\displaystyle \text{tg}\gamma =\frac{R_C}{r\left(1-Rc/RL\right)}\mathrm{.}}\end{array}$ Ha beállítjuk a rezonanciafeltételt, akkor $U=R_C{i}_0$ és $\gamma =-{90}^{\circ }$, tehát az izzólámpa-sorozat árama amplitúdó és fázis tekintetében ugyanaz, mintha egyszerűen csak a kondenzátort kapcsoltuk volna a váltófeszültségre.     $\begin{array}{c}{\displaystyle \text{<span style="font-style: italic;">4. ábra</span>}}\end{array}$   A vektordiagrammot 4. ábránk mutatja abban az esetben, ha $\omega =314{\text{sec}}^{-1}$, $C=2\cdot {10}^{-6}\text{farad}$, $R_C=1500$ ohm, $L=5$ henry, $R_L=1500$ ohm, tehát teljesül a rezonanciafeltétel) és például $r=1500$ ohm. Egymásra rajzoltuk a feszültségek és áramerősségek ábráját, mindegyiket a saját léptéke szerint; a feszültségeket folytonos, az áramerősségeket szaggatott vonalú nyilak mutatják. $i_{r0}=0\mathrm{,}1$ amperes értéket vettünk fel. Ugyanebben az irányban kellett felrajzolnunk az $A$, $B$ pontokra jutó 150 voltos amplitúdójú feszültséget. Ennek hatására a tekercsben a ${90}^{\circ }$-kal hátramaradó $i_{r0}$ amplitúdójú váltóáram keletkezik, amelyet $i_{r0}$-lal összegezve kapjuk $i_{C0}$-t. A kondenzátor feszültsége ehhez képest ${90}^{\circ }$-kal késik ($U_{C0}$). Végül ezt $U_{A{B}_0}$-lal egyesítve kapjuk a hálózati feszültség $U_0=150$ voltos amplitúdóját. Ha más ohmos ellenállás felhasználásával végezzük el a szerkesztést, az ábra részletei módosulnak, de $U_0$ végpontja ugyanoda esik.   3. Normális látású ember $25$ centimétertől végtelenig lát élesen. Milyen határok között fog élesen látni, ha szeme elé, a szemlencsétől $2$ centiméterre egy $1$ dioptriás gyűjtőlencsét helyez?   Megoldás. Ha a szem végtelenre van élesre állítva, akkor a szemlencsébe párhuzamos sugarak érkeznek. A szem elé gyűjtőlencsét téve akkor jutnak a szembe párhuzamosan a sugarak, ha a gyűjtőlencse fókusztávolsága 100 cm, tehát az élesen látás egyik határa: 100 cm a lencsétől, illetve 102 cm a szemtől számítva (5. ábra) 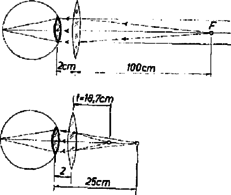    $\begin{array}{c}{\displaystyle \text{<span style="font-style: italic;">5. ábra</span>}}\end{array}$   Ha szemünk lencséje a 25 cm távolságból érkező sugarak számára van beállítva, akkor ez azt jelenti, hogy az 1 dioptriás lencse számára a virtuális képtávolság $-23$ cm. Ehhez $t$ tárgytávolság tartozik, amelyet a lencsetörvényből számítunk ki: $\begin{array}{c}{\displaystyle \frac{1}{100}=\frac{1}{t}+\frac{1}{-23}\mathrm{.}}\end{array}$ Innen $t=18\mathrm{,}7$ cm. Tehát ebben az esetben az élesen látás távolsága $18\mathrm{,}7$ cm a lencsétől, $20\mathrm{,}7$ cm szemünktől számítva.   A verseny eredménye: I. díjat nyert Tichy Géza (a budapesti Árpád gimnáziumban Peller József és Dömötör Gábor tanítványa), II. díjat nyert Abos Imre (a budapesti II. Rákóczi Ferenc gimnáziumban Petyerity Géza tanítványa), III. díjat nyert Major János (a budapesti Kandó Kálmán technikumban Bárczy Barnabás tanítványa). Dicséretet kaptak Gács Iván (a budapesti Bánki Donát technikumban Bangha József tanítványa), Lánc József (a budapesti I. István gimnáziumban Pálos Jenő tanítványa) és Máthé István (a budapesti Bánki Donát technikumban Galambos Imre tanítványa).