Kezdőlap


Cím:	Az 1964. évi Arany Dániel matematikai tanulóversenyek I. fordulóján kitűzött feladatok megoldása: Haladók (II. osztályosok) versenye
Szerző(k):	Lőrincz Pál , Surányi János
Füzet:	1964/december, 193 - 197. oldal	PDF \| MathML
Témakör(ök):	Arany Dániel

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Haladók (II. osztályosok) versenye

1. feladat. Számítsuk ki a következő összeget:

\begin{matrix} \sqrt[]{7 - \sqrt[]{48}} + \sqrt[]{5 - \sqrt[]{24}} + \sqrt[]{3 - \sqrt[]{8}} . \end{matrix}

(1)

Megoldás. Próbáljuk meg a négyzetgyök alatti különbségeket egy-egy különbség négyzetévé alakítani. Kézenfekvő egész számokból vont négyzetgyökök különbségére gondolni, tehát megpróbálni

\begin{matrix} {(\sqrt[]{a} - \sqrt[]{b})}^{2} = a + b - 2 \sqrt[]{a b} = a + b - \sqrt[]{4 a b} \end{matrix}

alakra hozni az egyes gyökjelek alatti értékeket. Az első tag esetében ekkor

a + b = 7

a b = 48 / 4 = 12

kell hogy fennálljon, és ennek a 3, 4 számpár megfelel. Mivel a négyzetgyök pozitív értékét keressük, így

\begin{matrix} \sqrt[]{7 - \sqrt[]{48}} = \sqrt[]{{(\sqrt[]{4} - \sqrt[]{3})}^{2}} = 2 - \sqrt[]{3} . \end{matrix}

Hasonlóan a második tag esetében az

a + b = 5

a b = 6

egyenletrendszer adódik; megoldása 2, 3, s így

\begin{matrix} \sqrt[]{5 - \sqrt[]{24}} = \sqrt[]{3} - \sqrt[]{2}; \end{matrix}

a harmadik tagnál pedig

a + b = 3

a b = 2

megoldása az 1, 2 számpár, s így

\begin{matrix} \sqrt[]{3 - \sqrt[]{8}} = \sqrt[]{2} - 1. \end{matrix}

Ezeket összeadva

\begin{matrix} \sqrt[]{7 - \sqrt[]{48}} + \sqrt[]{5 - \sqrt[]{24}} + \sqrt[]{3 - \sqrt[]{8}} = 2 - \sqrt[]{3} + \sqrt[]{3} - \sqrt[]{2} + \sqrt[]{2} - 1 = 1. \end{matrix}

Megjegyzés. A fenti eljárással általában különbséggé alakítható egy

\sqrt[]{u \pm \sqrt[]{v}}

alakú kifejezés (ahol

u

v > 0

u^{2} > v

). Ez esetben az előbbi gondolatmenet az

a + b = u

4 a b = v

egyenletrendszerre vezet. Ennek a gyökei az

x^{2} - u x + v / 4 = 0

egyenletnek tesznek eleget, tehát az

(u \pm \sqrt[]{u^{2} - v}) / 2

értékek, így a

\begin{matrix} \sqrt[]{u \pm \sqrt[]{v}} = \sqrt[]{\frac{u + \sqrt[]{u^{2} - v}}{2}} \pm \sqrt[]{\frac{u - \sqrt[]{u^{2} - v}}{2}} \end{matrix}

azonossághoz jutunk.

2. feladat. Legyen egy derékszögű háromszög hosszabbik befogója

1

, a rövidebb

t

hosszúságú. Legyen egy másik derékszögű háromszög két befogójának hossza

2 t

és

1 - t^{2}

. Mutassuk ki, hogy a második háromszögnek a

2 t

hosszúságú befogóval szemközti szöge az eredeti háromszög legkisebb szögének kétszerese!

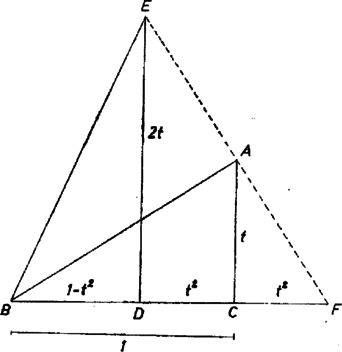1. ábra

I. megoldás. Rajzoljunk

C

-nél derékszögű háromszöget

A C = t

B C = 1

hosszúságú befogókkal; mérjük rá a

B C

befogóra a

B D = 1 - t^{2}

hosszúságot, majd a

D

-ben a

B C

egyenesre emelt merőlegesre az egyenes

A

-t tartalmazó oldalán a

D E = 2 t

hosszúságot. Ekkor azt kell bebizonyítanunk, hogy

E B D ∢ = 2 A B C ∢

, vagyis hogy

A B

felezi az

E B D

szöget. Ez következik abból, ha megmutatjuk, hogy az

E A

egyenes az

E B D

szögtartományból egyenlő szárú háromszöget vág le, amelynek

A B

a szimmetriatengelye.
Jelöljük az

E A

és

B D

egyenes metszéspontját

F

-fel.

A C

F E D

háromszög középvonala, mert párhuzamos

E D

-vel, és fele akkora. Ha ugyanis

A

és

C

közelebb, ill. messzebb volna

F

-től, mint a megfelelő oldal felezőpontja, akkor összekötő egyenesük is kisebb, ill. nagyobb volna, mint

E D

fele. Ezek szerint

E A = A F

, és

F C = C D = C B - D B = 1 - (1 - t^{2}) = t^{2}

. Az

F A C

és

A B C

háromszögek hasonlók, mert mindkettő

C

-nél derékszögű, és a befogók aránya egyenlő:

\begin{matrix} \frac{A C}{F C} = \frac{t}{t^{2}} = \frac{1}{t} = \frac{B C}{A C} . \end{matrix}

A megfelelő befogók egymáshoz képest ugyanolyan irányban

90^{\circ}

-kal vannak elforgatva, így ugyanez áll az átfogókra is:

F A ⊥ A B

.
Ezzel beláttuk, hogy

A B

E F

szakaszt felező és arra merőleges egyenes, tehát az

E B F

háromszög szimmetriatengelye; így az

E B F ∢ = E B D ∢

szögfelezője.

II. megoldás. Rajzoljuk meg az

A B C

és

E B D

háromszögeket ugyanúgy, mint az előző megoldásban. Messe az

A

-n át

B C

-vel párhuzamosan húzott egyenes

B E

-t és

D E

-t

G

-ben és

H

-ban.

G H

B D E

háromszög középvonala, mert

D H = C A = t = \frac{1}{2} D E

, és

G H ‖ B D

, tudjuk továbbá, hogy a középvonal is párhuzamos

B D

-vel, és

H

-n át csak egy ilyen párhuzamos húzható. Így egyrészt Pythagorász tétele szerint (2. ábra)

\begin{matrix} B G = \frac{1}{2} B E = \frac{1}{2} \sqrt[]{B D^{2} + D E^{2}} = \frac{1}{2} \sqrt[]{{(1 - t^{2})}^{2} + 4 t^{2}} = \frac{1 + t^{2}}{2}, \end{matrix}

másrészt

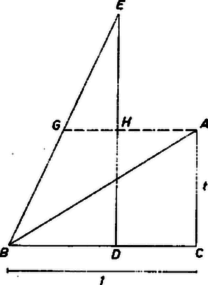\begin{matrix} G A = G H + H A = \frac{B D}{2} + D C = \frac{1 - t^{2}}{2} + [1 - (1 - t^{2})] = \frac{1 + t^{2}}{2} . \end{matrix}

2. ábra

Eszerint az

A B G

háromszög egyenlő szárú, így ‐ felhasználva azt is, hogy

G A ‖ B C

‐

\begin{matrix} E B A ∢ = G B A ∢ = G A B ∢ = A B D ∢, \end{matrix}

tehát

E B D ∢ = 2 A B D ∢

, és ezt kellett bizonyítanunk.
(Tulajdonképpen azt bizonyítottuk, hogy a

G

közepű

(1 + t^{2}) / 2

sugarú kör

A

pontjában érinti

A C

-t, tehát

A

az érintővel párhuzamos húrhoz tartozó

E D

ív felezőpontja.)

III. megoldás. Ismét az előző megoldásban látott módon helyezzük el a két háromszöget. Jelöljük

A B

és

D E

metszéspontját

M

-mel. Elég megmutatnunk, hogy

M

ugyanolyan arányú két részre osztja

D E

-t, mint a szögfelező, ugyanis ha egy

P

pont a

D E

szakaszon

D

-től

E

felé mozog, akkor a

D P / P E

arány számlálója nő, nevezője csökken, és így a tört értéke állandóan nő, egy értéket csak egyszer vesz fel.
Tudjuk, hogy a szögfelezőre nézve a szóban forgó osztásarány megegyezik a

B D / B E

aránnyal, mivel pedig

\begin{matrix} B E = \sqrt[]{B D^{2} + D E^{2}} = \sqrt[]{{(1 - t^{2})}^{2} + {(2 t)}^{2}} = 1 + t^{2}, \end{matrix}

így a szögfelező által kimetszett szeletek aránya

(1 - t^{2}) / (1 + t^{2})

3. ábra

A B C

és

M B D

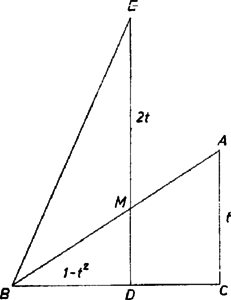háromszögek hasonlók, így befogóik arányára:

\begin{matrix} \frac{M D}{B D} = \frac{A C}{B C}, M D = \frac{A C \cdot B D}{B C} = t (1 - t^{2}) . \end{matrix}

Ezt felhasználva nyerjük, hogy

\begin{matrix} \frac{D M}{M E} = \frac{t (1 - t^{2})}{2 t - t (1 - t^{2})} = \frac{t (1 - t^{2})}{t (1 + t^{2})} = \frac{B D}{B E} . \end{matrix}

M

pont tehát ugyanolyan arányú részekre osztja

D E

-t, mint a szögfelező, és ezzel beláttuk, hogy

B M

azonos az

E B D

szög felező egyenesével.

3. feladat. Az óramutató, a percmutató és a másodpercmutató közös tengely körül forognak. Adjuk meg azokat az időpontokat, amikor a másodpercmutató felezi az óramutató és a percmutató által bezárt szöget!

I. megoldás. Célszerű a szögmérés egységéül az óra számlapjának percbeosztását, azaz a teljes körülfordulás 60-adrészét választani.
Két mutató az óra számlapját két körcikkre osztja, ezeket ugyanannak az egyenesnek a tengelyből induló két félegyenese felezi. Az óramutatók fedése esetén az egyik körcikk a teljes körlemezbe, a másik a kör egy sugarába megy át; ennek az egyenese tekinthető ilyenkor a szögfelezőnek.
Egy a feltételeket kielégítő

H_{1}

helyzetből kiindulva határozzuk meg azt az időtartamot (másodpercben mérve), ami alatt a legközelebbi megfelelő

H_{2}

helyzetbe jutnak a mutatók. A másodpercmutató

t

másodperc alatt

t

beosztással mozdul el; a

H_{2}

helyzetben a szögfelezőnek a másik félegyenesével kerül fedésbe, mint a

H_{1}

helyzetben. Tekintetbe kell vennünk azt is, hogy időközben a szögfelező helyzete is megváltozott. Azt az ívet vizsgálva, amelyik az óramutatótól a mutatók járása irányában a percmutató felé terjed,

t

másodperc alatt az óramutató

\frac{5}{60 \cdot 60} \cdot t = \frac{t}{720}

beosztást halad előre, a percmutató

\frac{t}{60}

beosztást.

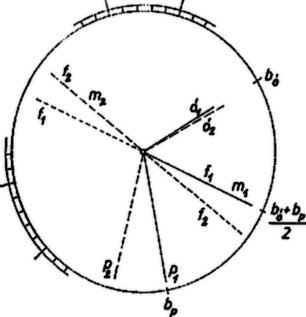4. ábra

Ha a

H_{1}

helyzetben az óramutató a

b_{0}

beosztásnál, a percmutató pedig

b_{p}

-nél volt, akkor a szögfelező helyzete

(b_{0} + b_{p}) / 2

volt,

t

másodperc múlva pedig

(b_{0} + t / 720 + b_{p} + t / 60) / 2 = (b_{0} + b_{p}) / 2 + 13 t / 1440

, tehát a szögfelező

13 t / 1440

beosztással jutott tovább.¹ Azt, hogy

i

idő elteltével a másodpercmutató a szögfelezőnek a

H_{1}

helyzetben fedett félegyenesével ellentétes irányú félegyenesével került fedésbe, az

\begin{matrix} i = \frac{13 i}{1440} + 30 \end{matrix}

egyenlet fejezi ki. Innen

i = \frac{1440}{1427} \cdot 30 = 30 + \frac{390}{1427} mp

. Ez nem tartalmazza a

H_{1}

helyzetet jellemző adatokat, így azt nyertük, hogy bármely két egymásutáni, a feltételeket kielégítő helyzet közt a nyert

i

idő telik el.
A három mutatónak

0

óra

0

perc

0

másodperckor elfoglalt helyzete kielégíti a követelményt, tehát az összes megfelelő időpontok

i

többszörösei:

\begin{matrix} t = k \cdot (30 + \frac{390}{1427}) mp = \\ = \frac{43 200 k}{1427} mp = \frac{720 k}{1427} perc, \end{matrix}

ahol

k

egész szám. Ha

k = 1427

, akkor

t = 720 perc = 12 óra

. És ettől kezdve ismétlődnek a mutatóállások;

k = 0, 1, 2, ..., 1426

értékekhez viszont csupa különböző mutató-állások tartoznak, hiszen az óramutató egyszer jár körbe, tehát biztosan mindig más helyzetben van.

II. megoldás. Azt az időt, ami két egymás utáni megfelelő helyzet közt telik el, kiszámíthatjuk a következő módon is: Az olyan helyzetek időpontjait keressük, amelyekben a szögfelező egyenese és a másodpercmutató egyenese fedi egymást. Ez 12 óra alatt annyiszor következik be, amennyivel többször kerül az utóbbi kiindulási helyzetébe, mint az előbbi, tekintettel arra, hogy a 12 óra végén mindkét egyenes éppen közös kiindulási helyzetébe tér vissza.
A másodpercmutató egyenese félpercenként kerül vissza eredeti helyzetébe, tehát 12 óra alatt

12 \cdot 60 \cdot 2 = 1440

-szer. A szögfelező egyenese, mint láttuk,

13 / 1440

beosztást halad előre másodpercenként, tehát 12 óra alatt

12 \cdot 60 \cdot 60 \cdot 13 / 1440 = 30 \cdot 13

beosztásnyi utat tesz meg. Ez alatt 13-szor kerül fedésbe eredeti helyzetével, miután ez 30 beosztásnyi elforduláskor következik be. A másodpercmutató egyenese tehát 12 óra alatt

1440 - 13 = 1427

-szer találkozik a szögfelező egyenesével, s így két egymás utáni találkozás közt

12 \cdot 60 \cdot 60 / 1427 = 30 + 390 / 1427

másodperc telik el.

Lőrincz Pál, Surányi János

¹A 4. ábra az elfordulásokat nagyítva tünteti fel.