Cím: Az 1964. évi Arany Dániel matematikai tanulóversenyek I. fordulóján kitűzött feladatok megoldása: Kezdők (I. osztályosok) versenye
Szerző(k):  Lukács Ottó ,  Scharnitzky Viktor 
Füzet: 1964/november, 114 - 117. oldal  PDF  |  MathML 
Témakör(ök): Arany Dániel

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

1. feladat. Egy üzemben négy dolgozó között egy kerek százasokban megállapított összeget osztanak ki jutalom gyanánt. Közlik velük, hogy választhatnak két elv szerinti felosztás között. Az első elv szerint az összeget havi fizetéseik arányában osztanak fel, a második elv szerint az eddig munkában töltött éveik arányában. ‐ Mindegyik dolgozó a részére kedvezőbb elvre szavazott, így a szavazás nem hozott döntést. Végül megegyeztek, hogy mindegyik dolgozó a két elv szerinti jutalmának átlagát kapja, 10 Ft-ra kerekítve. Így a legfiatalabb 980 Ft-ot kapott. Mennyit kaptak a többiek, ha egymás után 14, 17, 21, illetőleg 31 éve dolgoznak, és mostani fizetésük sorra 1500 Ft, 1600 Ft, 1800 Ft és 2300 Ft ?

 

Megoldás. Ha a jutalom összegét a fizetések arányában osztanák szét, akkor az egyes dolgozók rendre az összeg 15/72, 16/72, 18/72, ill. 23/72 részét kapnák, a munkában eltöltött évek száma arányában történő felosztás esetén pedig rendre 14/83, 17/83, 21/83, ill. 31/83 részét. A kétféle hányadrészek átlaga rendre
12(1572+1483)=225311952,255211952,300611952,414111952,
ezekből a megállapodás szerint kifizetett jutalmakat úgy kapjuk meg, hogy megszorozzuk az átlagokat a szétosztandó x összeggel, és a szorzatokat 10 Ft-ra kerekítjük.
A legfiatalabb jutalmazott részére a mondott szorzás útján 975 és 985 Ft közötti értéknek kellett adódnia, mert a közölt kerekítési elv szerint ezekből az értékekből adódik 980 Ft. Eszerint
975≤225311952x≤985,
(az egyenlőséget mindkét helyen megengedjük, mert 980-ban a tízesek száma páros). Ezt x együtthatójának reciprokával szorozva
51726842253≤x≤52257952253
(ugyanis a használt szorzó pozitív).
Az x-re nyert korlátok között egyetlen kerek százas van, így x=5200 Ft.
Ezt felhasználva a fenti számítási elv alapján a további három dolgozónak járó jutalom rendre 1110 Ft, 1310 Ft, ill. 1800 Ft. A kerekítés során fel-, ill. lefelé végzett kiigazítások kiegyenlítik egymást, a kifizetett jutalmak öszege 5200 Ft.
 

2. feladat. Oldjuk meg a következő egyenletet:
(a+b)(c-x)a2-(b+c)(x-2c)bc-(c+a)(c-2x)ac=(a+b)cab+2.(1)
Vizsgáljuk meg azt az esetet, ha a:b:c=6:3:4.
 

Megoldás. Az a, b, c értékek egyike sem lehet 0, különben az egyenletnek nem volna értelme. Így a törteket eltávolítva a következő, az eredetivel egyenértékű egyenletet kapjuk:
(a+b)(c-x)bc-(b+c)(x-2c)a2-(c+a)(c-2x)ab==(a+b)ac2+2a2bc.


Ebből pedig a szokásos rendezési lépésekkel a következő egyenletet kapjuk:
x(a2b-a2c+abc-b2c)=c(a2b-a2c+abc-b2c).
Ha x együtthatója nem 0, akkor x=c.
Ha pedig x együtthatója 0, akkor az egyenletnek bármely szám megoldása. Ez következik be a külön vizsgálandó esetben; az a:b:c=6:3:4 arányosság ugyanis azt jelenti, hogy alkalmas u értékkel a=6u, b=3u, c=4u, és ezt behelyettesítve x együtthatója, és a jobb oldal 0 lesz, ill. az eredeti egyenletbe helyettesítve a bal oldalon x kiesik, és mindkét oldal értéke 4 lesz; azonossághoz jutunk.
 

3. feladat. Adott két egybevágó szabályos hatszög. Körzőbe vesszük oldaluk negyedrészét, és félköröket rajzolunk minden oldal felezőpontja körül az első hatszög esetében kifelé, a második esetében befelé; továbbá körívet mindegyik csúcs körül az első esetben a hatszög szögeinek terében, a második esetben pedig a hatszögön kívül, oldaltól oldalig. Tekintsük most azt a két idomot, amelyet az egymáshoz kapcsolódó ívek és félkörök határolnak. Melyik idomnak nagyobb a területe?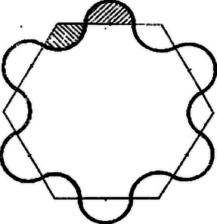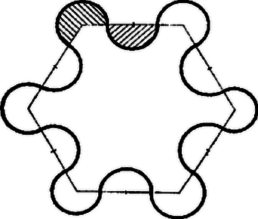
 
 
1. ábra
 

 
 
2. ábra
 

Megoldás. Az első idom területét úgy kaphatjuk meg a hatszög területéből, hogy hozzáadjuk a kinyúló hat félkör ‐ azaz három kör ‐ területét, és elvesszük a befelé rajzolt hat ugyanakkora sugarú harmadkör ‐ azaz két kör ‐ területét (1. ábra). Így a hatszöget egy kör területével növeltük.
A második idom területe hat kétharmad kör ‐ azaz négy kör ‐ területének hozzáadásával és hat ugyanilyen sugarú félkör ‐ azaz három kör ‐ területének elhagyásával keletkezik a hatszög területéből (2. ábra). Tehát a hatszög területénél ugyancsak egy olyan kör területével nagyobb, amelyiknek sugara a hatszög oldalának a negyede. Így a két idom területe egyenlő.
 

Megjegyzés. Könnyű belátni, hogy a feladat eljárását 6-szög helyett akárhány oldalú szabályos sokszögre végezve mindkét idom területe továbbra is egy kör területével növekszik. (Háromszög esetén a második módon egy négy részre széteső idomot kapunk, 3. ábra.)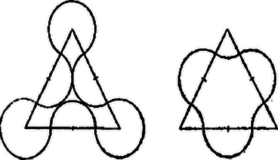
 
 
3. ábra
 

Még általánosabban, ha tetszés szerinti (önmagát nem metsző) sokszöget veszünk 2 példányban, és az egyik oldalainak középpontjai körül kifelé, a másikéi körül befelé rajzolunk egyenlő sugárral félköröket, továbbá ugyanezzel a sugárral az előbbi csúcsai köré befelé, az utóbbié köré kifelé rajzolunk köríveket oldaltól oldalig, a kör sugarát úgy választva, hogy a rajzolt körívek ne nyúljanak egymásba, akkor a két módosított idom területe egyenlő (4. ábra).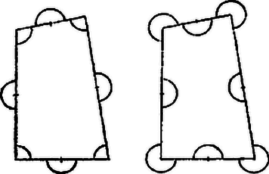
 
 
4. ábra
 

Valóban legyen a sokszög oldalszáma n, egy kör területe t, a csúcsok köré befelé rajzolt körcikkek területeinek összege B, a külső körcikkeké K, akkor nyilván B+K=nt. Az első idom területét n⋅t2-B-vel változtattuk meg, a másodikét pedig
K-n⋅t2=(nt-B)-n⋅t2=n⋅t2-B
-vel, tehát ugyanannyival, és ezt akartuk belátni. Könnyen igazolható az is, hogy mindig egy kör területével növekedik a sokszög területe.