Kezdőlap


Cím:	Az 1964. évi Országos Középiskolai Matematikai Tanulmányi Verseny II. fordulóján kitűzött feladatok megoldása
Szerző(k):	Surányi János
Füzet:	1964/november, 105 - 114. oldal	PDF \| MathML
Témakör(ök):	OKTV

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

1. feladat. Bizonyítandó, hogy ha $α$ , $β$ és $γ$ egy háromszög szögei, akkor

\begin{matrix} cos α + cos β + cos γ < 2. \end{matrix}

I. megoldás. Írjunk

γ

helyébe

180^{\circ} - (α + β)

-t, majd igyekezzünk szorzattá alakítani:

\begin{matrix} cos α + cos β + cos γ = cos α + cos β - cos α cos β + sin α sin β = \\ = cos α + (1 - cos α) cos β + sin α sin β = \\ = 1 - (1 - cos α) + (1 - cos α) cos β + sin α sin β = \\ = 1 - (1 - cos α) (1 - cos β) + sin α sin β . \end{matrix}

Itt a második tag nem pozitív, mert a koszinusz-függvény nem vesz fel

1

-nél nagyobb értéket, a harmadik pedig kisebb

1

-nél, mert egyik tényezője sem nagyobb

1

-nél, de nem lehet mindkettő egyszerre

1

sem (nem lehet

α

is,

β

90^{\circ}

). Így

\begin{matrix} cos α + cos β + cos γ < 2, \end{matrix}

és ezt akartuk bizonyítani.

II. megoldás. Az állítás helyes, ha a háromszög nem hegyesszögű, mert ekkor az egyik tag nem pozitív, a másik kettő mindegyike pedig

1

-nél kisebb.
Hegyesszögű háromszögben válasszuk a betűzést úgy, hogy

γ

és a vele szemben levő

A B = c

oldal legyen a legkisebb, illetve a legkisebbek egyike. Jelöljük továbbá

γ

csúcsát

C

-vel, az

A C

B C

oldalakat

b

-vel, ill.

a

-val; legyen

C

merőleges vetülete az

A B

egyenesen

C_{1}

, ez az oldal belső pontja. Így

\begin{matrix} c = A C_{1} + C_{1} B = b cos α + a cos β . \end{matrix}

Innen, mivel feltevés szerint

a ≧ c

b ≧ c

, így

\begin{matrix} 1 = \frac{b}{c} cos α + \frac{a}{c} cos β \geq cos α + cos β; \end{matrix}

a harmadik szögre

cos γ < 1

, tehát helyes az állítás hegyesszögű háromszögben is.

III. megoldás. A bizonyítandó egyenlőtlenség, mint az előző megoldásban is láttuk, nyilvánvalóan helyes, ha a háromszög nem hegyesszögű. Hegyesszögű háromszögre

α_{1} = 90^{\circ} - α

β_{1} = 90^{\circ} - β

γ_{1} = 90^{\circ} - γ

pozitív hegyesszögek, melyek összege

90^{\circ}

, és

\begin{matrix} cos α + cos β + cos γ = sin α_{1} + sin β_{1} + sin γ_{1} . \end{matrix}

Ezt az összeget szemléltethetjük a következő módon: egységnyi sugarú

O P Q

negyedkörbe rajzoljuk be az

α_{1}

, ill.

β_{1}

nagyságú

P O A

A O B

szögeket (1. ábra).

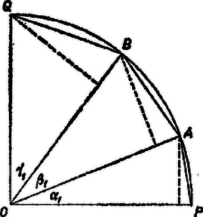1. ábra

Ekkor

B O Q ∢ = γ_{1}

, és a

P O A

A O B

B O Q

háromszögekben a sugár alkotta oldalakra merőleges magasság hossza rendre

sin α_{1}

sin β_{1}

sin γ_{1}

, így a vizsgálandó összeg az

O P A B Q

ötszög területének kétszeresével egyenlő, tehát kisebb, mint az egységnyi sugarú félkör területe,

π / 2

. Hegyesszögű háromszögre tehát

\begin{matrix} cos α + cos β + cos γ < \frac{π}{2} (< 1, 571) . \end{matrix}

IV. megoldás. Alakítsuk két koszinusz összegét szorzattá:

\begin{matrix} cos β + cos γ = 2 cos \frac{β + γ}{2} cos \frac{β - γ}{2} = 2 sin \frac{α}{2} cos \frac{β - γ}{2} \leq 2 sin \frac{α}{2}, \end{matrix}

mert mindkét tényező pozitív, hiszen

α / 2

és

| β - γ | / 2

hegyesszögek. Fejezzük ki

cos α

-t is a fele akkora szög szinuszával, akkor azt nyerjük, hogy

\begin{matrix} cos α + cos β + cos γ \leq 1 - 2 sin^{2} \frac{α}{2} + 2 sin \frac{α}{2} = \frac{3}{2} - \frac{1}{2} {(1 - 2 sin \frac{α}{2})}^{2} . \end{matrix}

A második tag nem lehet pozitív, így a bizonyítandó állításon túlmenően azt bizonyítottuk be, hogy

\begin{matrix} cos α + cos β + cos γ \leq \frac{3}{2} . \end{matrix}

(1)

Itt akkor érvényes az egyenlőség jele, ha egyrészt

cos ((β - γ) / 2) = 1

, másrészt

sin (α / 2) = 1 / 2

. Az első egy háromszög szögeire csak akkor teljesül, ha

β = γ

, a második akkor, ha

α = 60^{\circ}

; ekkor az első feltétel szerint

β = γ = 60^{\circ}

, azaz a háromszög szabályos.
Az (1) egyenlőtlenségben tehát szabályos háromszögre egyenlőség, más háromszögekre a ,,kisebb'' jel érvényes.

Megjegyzés. Az előző megoldás ábrája alapján finomabb elemzéssel szintén bizonyítható az (1) egyenlőtlenség hegyesszögű háromszögre, és kiterjeszthető a meggondolás nem hegyesszögű háromszögekre is.

V. megoldás. Fejezzük ki a szögek koszinuszát a koszinusz-tétel alapján az oldalakkal. Vizsgáljuk először két koszinusz összegét:

\begin{matrix} cos α + cos β = \frac{- a^{2} + b^{2} + c^{2}}{2 b c} + \frac{a^{2} - b^{2} + c^{2}}{2 a c} = \\ = \frac{a^{2} - b^{2}}{2 c} (\frac{1}{a} - \frac{1}{b}) + \frac{c}{2} (\frac{1}{a} + \frac{1}{b}) = \frac{1}{2} (\frac{c}{a} + \frac{c}{b}) - \frac{(a + b) {(a - b)}^{2}}{2 a b c} . \end{matrix}

Mindhárom szögpárra felírva a megfelelő kifejezést és összeadva azokat, a pozitív tagok összegében fellép miden törttel a reciproka is, így az összeg a következőképpen alakítható tovább:

\begin{matrix} 2 (cos α + cos β + cos γ) = \frac{1}{2} (\frac{a}{b} + \frac{b}{a} + \frac{b}{c} + \frac{c}{b} + \frac{c}{a} + \frac{a}{c}) - \\ - \frac{(a + b) {(a - b)}^{2} + (b + c) {(b - c)}^{2} + (c + a) {(c - a)}^{2}}{2 a b c} = \\ = 3 + \frac{1}{2} (\frac{{(a - b)}^{2}}{a b} + \frac{{(b - c)}^{2}}{b c} + \frac{{(c - a)}^{2}}{a c}) - \\ - \frac{(a + b) {(a - b)}^{2} + (b + c) {(b - c)}^{2} + (c + a) {(c - a)}^{2}}{2 a b c} = 3 - \\ - \frac{(a + b - c) {(a - b)}^{2} + (b + c - a) {(b - c)}^{2} + (c + a - b) {(c - a)}^{2}}{2 a b c} \leq 3, \end{matrix}

ugyanis mindegyik négyzet szorzója pozitív, mert a háromszög két oldalának az összege nagyobb, mint a harmadik oldal. Így

\begin{matrix} cos α + cos β + cos γ \leq \frac{3}{2} . \end{matrix}

(1)

Itt akkor áll egyenlőség, ha a fenti tört számlálójában

a - b = b - c = c - a = 0

, azaz szabályos háromszögre.

Megjegyzés: többen észrevették a bal oldal következő átalakítási lehetőségét:

\begin{matrix} \frac{a^{2} b + a^{2} c + a b^{2} + b^{2} c + a c^{2} + b c^{2} - a^{3} - b^{3} - c^{3}}{2 a b c} = \\ = \frac{(a + b - c) (a - b + c) (- a + b + c) + 2 a b c}{2 a b c} . \end{matrix}

Innen Heron képletét, az

a b c = 4 r t

és

t = ϱ s

összefüggéseket felhasználva, ahol

s

a kerület felét,

t

a háromszög területét,

r

és

ϱ

a körülírt és beírt kör sugarát jelöli, a következőt nyerjük:

\begin{matrix} cos α + cos β + cos γ = 1 + \frac{16 t^{2}}{16 r t s} = 1 + \frac{ϱ}{r} . \end{matrix}

Világos, hogy

ϱ < r

, amiből következik a feladat állítása. Az is belátható (trigonometria felhasználása nélkül is), hogy

ϱ \leq r / 2

, amiből (1) következik.

2. feladat. Öt egész szám számtani sorozatot alkot. Akár az első négy tag köbeinek összegét vesszük, akár az utolsó négy tag köbeinek összegét, mindkétszer a figyelembe vett tagok összege négyzetének

16

-szorosát kapjuk. Határozzuk meg a számokat.

I. megoldás. Jelöljük a középső számot

c

-vel, a számtani sorozat különbségét

d

-vel, ekkor a feladat feltételei:

\begin{matrix} {(c - 2 d)}^{3} + {(c - d)}^{3} + c^{3} + {(c + d)}^{3} = & (1) \\ = 16 {(c - 2 d + c - d + c + c + d)}^{2} = 16 {(2 (2 c - d))}^{2}, \\ {(c - d)}^{3} + c^{3} + {(c + d)}^{3} + {(c + 2 d)}^{3} = & (2) \\ = 16 {(c - d + c + c + d + c + 2 d)}^{2} = 16 {(2 (2 c + d))}^{2} . \end{matrix}

A második az elsőből megkapható úgy, hogy

d

helyébe

- d

-t írunk (és a tagokat fordított sorrendbe írjuk), ez felhasználható lesz az átalakítások meggyorsítására. Az (1) egyenletet rendezve és

2

-vel egyszerűsítve

\begin{matrix} 2 c^{3} - 3 c^{2} d + 9 c d^{2} - 4 d^{3} = 128 c^{2} - 128 c d + 8 d^{2} . \end{matrix}

Hasonlóan (2)-ből

\begin{matrix} 2 c^{3} + 3 c^{2} d + 9 c d^{2} + 4 d^{3} = 128 c^{2} + 128 c d + 8 d^{2} . \end{matrix}

Vonjuk le a második egyenletből az elsőt és osszunk

2

-vel:

\begin{matrix} 3 c^{2} d + 4 d^{3} = 128 c d . \end{matrix}

Ez teljesül, ha

d = 0

. Ekkor (1)-ből

\begin{matrix} 4 c^{3} = 256 c^{2}, c = 0 vagy c = 64. \end{matrix}

d \neq 0

, akkor a

\begin{matrix} 3 c^{2} - 128 c + 4 d^{2} = 0 \end{matrix}

egyenletnek kell teljesülnie. Szorozzunk

3

-mal és egészítsük ki az első két tagot teljes négyzetté:

\begin{matrix} {(3 c - 64)}^{2} + 3 {(2 d)}^{2} = 2^{12} . \end{matrix}

(3)

Itt, ha

c

egész, a bal oldal első tagja nem

0

, és feltevésünk szerint a második sem. Legyen

3 c - 64 = 2^{k} u

2 d = 2^{l} v

, ahol

u

v

páratlan és

k, l < 6

. Nem lehet

k

és

l

különböző, mert akkor

2

alkalmas hatványának kiemelése után

1

-nél nagyobb páratlan szám marad vissza, s így nem keletkezhet a jobb oldali

2^{12}

érték. Ha

k = l

, akkor az

\begin{matrix} u^{2} + 3 v^{2} = 2^{12 - 2 k} = 4^{6 - k} \end{matrix}

egyenlethez jutunk, amelynek páratlan

u

és

v

-ből álló megoldását keressük. Ismeretes, hogy páratlan szám négyzete

8

-cal osztva

1

-et ad maradékul. Az egyenlet bal oldala eszerint

8

-cal osztva

4

-et ad maradékul, tehát csak úgy lehet

2

-nek egy hatványa, ha egyenlő

4

-gyel, azaz

k = 5

u = \pm 1

v = \pm 1

, tehát

\begin{matrix} 3 c - 64 = \pm 32, 2 d = \pm 32. \end{matrix}

Az első egyenletből csak pozitív előjel mellett kapunk egész

c

-t:

\begin{matrix} c = 32, d = \pm 16. \end{matrix}

A feladat feltételeinek tehát a

\begin{matrix} 0, & 0, & 0, & 0, & 0 & 64, & 64, & 64, & 64, & 64 \\ 0, & 16, & 32, & 48, & 64 & 64, & 48, & 32, & 16, & 0 \end{matrix}

sorozatok felelhetnek meg, és a számításokat elvégezve azt találjuk, hogy ezek valóban meg is felelnek.

II. megoldás. Az előző megoldás jelöléseit használva az (1) egyenlet bal oldalán az első és utolsó, továbbá a második és harmadik tag összegét alakítsuk át az

a^{3} + b^{3} = (a + b) (a^{2} - a b + b^{2})

azonosság alapján. Ekkor a bal oldal így alakul:

\begin{matrix} (2 c - d) [{(c - 2 d)}^{2} - (c - 2 d) (c + d) + {(c + d)}^{2}] + (2 c - d) [{(c - d)}^{2} - \\ - (c - d) c + c^{2}] = (2 c - d) (2 c^{2} - 2 c d + 8 d^{2}) . \end{matrix}

Így az egyenletet

0

-ra redukálva

2 (2 c - d)

-t kiemelhetünk:

\begin{matrix} 2 (2 c - d) (c^{2} - c d + 4 d^{2} - 64 c + 32 d) = 0. \end{matrix}

Hasonlóan a (2) egyenletből

\begin{matrix} 2 (2 c + d) (c^{2} + c d + 4 d^{2} - 64 c - 32 d) = 0. \end{matrix}

d = 2 c

, akkor az előbbi egyenlet teljesül, az utóbbi így alakul:

\begin{matrix} 8 c^{2} (19 c - 128) = 0. \end{matrix}

(4)

Ennek egész gyöke csak

c = 0

, amiből

d = 0

.
A

d = - 2 c

esetben az előbbi egyenlet megy át (4)-be, s így újabb megoldást nem kapunk.
Ha

d \neq \pm 2 c

, akkor a következő egyenletrendszernek kell teljesülnie:

\begin{matrix} c^{2} - c d + 4 d^{2} - 64 c + 32 d = 0, \\ c^{2} + c d + 4 d^{2} - 64 c - 32 d = 0. \end{matrix}

Az egyenletek összegének felét és különbségének felét véve az eredetivel ekvivalens egyenletrendszert kapunk, hiszen az utóbbiak különbsége, ill. összege az eredeti egyenleteket adja:

\begin{matrix} c^{2} + 4 d^{2} - 64 c = c (c - 64) + 4 d^{2} = 0, (c - 32) d = 0. \end{matrix}

Az utóbbi egyenletből vagy

c = 32

, vagy

d = 0

kell, hogy teljesüljön. Az első esetben az előbbi egyenletből

\begin{matrix} 4 d^{2} = 32^{2} d = \pm 16, \end{matrix}

az utóbbi esetben pedig

\begin{matrix} c = 0, vagy c = 64. \end{matrix}

Ezek az előbbi megoldásban talált számtani sorozatokra vezetnek.

Megjegyzések. 1. A feltételek két ismeretlenre két egyenletet adnak, ezekből az ismeretlenekre véges sok értékpár adódik. Mint a II. megoldás mutatja, nem szükséges lényegesen kihasználni a számok egész voltát, mindössze a többi feltételeket kielégítő

\begin{matrix} - 384 / 19, - 128 / 19, 128 / 19, 384 / 19, 640 / 19 \end{matrix}

és az ennek megfordításával keletkező sorozat kizárására.
2. Az I. megoldásban az (1) és (2)-ből keletkező (3) egyenletet oldottuk meg a keresett számok egész voltát lényegesen kihasználva. A közben felmerült

c = 32 / 3

d = \pm 16

értékpárokhoz tartozó számtani sorozatok nem csak nem állnak egészekből, de a feladat többi feltételét sem elégítik ki. Ez nem meglepő, hiszen a megoldott (3) egyenlet nem ekvivalens az (1) és (2)-ből álló egyenletrendszerrel. Ezért az I. megoldásnál szükséges a nyert sorozatokra a követelmények teljesülésének ellenőrzése. Az előző pontban említett nem egész sorozat viszont az I. megoldásban nem jelentkezett, amit az magyaráz, hogy ott csak egész megoldást kerestünk,

c = 128 / 19

d = \pm 256 / 19

-höz pedig a (3) egyenletnek nem egész megoldása tartozik.

3. feladat. Melyek azok a konvex poliéderek, amelyeknek bármely négy nem egy síkban levő csúcsa ugyanakkora térfogatú háromoldalú gúlát határoz meg ?

I. megoldás. 1. Keressük először az olyan poliédereket, amelyeknek minden határlapja háromszög. Legyen a poliéder egy

A B

élén átmenő két határlap

A B C

és

A B D

. Az

A B C D

háromoldalú gúla tekinthető a feladat követelményeit kielégítő poliédernek (nem választható ki több különböző csúcsnégyes, 2. a. ábra).

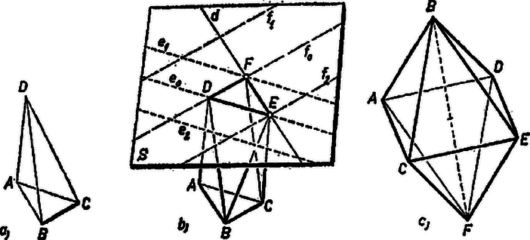2. ábra

Ha a poliédernek négynél több csúcsa van, akkor minden további csúcsnak a

D

-n átmenő,

A B C

-vel párhuzamos

S

síkban kell lennie, mert az

A B C

síkban több csúcs nincs, a többi csúcs ennek a síknak ugyanazon oldalán van, mint

D

, és a síktól ugyanakkora távolságra, mint

D

, mert különben az

A

B

C

csúcsokkal

A B C D

-étől különböző térfogatú gúlát alkotna. Ugyanígy benne vannak a további csúcsok a

C

-n átmenő,

A B D

-vel párhuzamos síkban is, tehát a két sík

d

metszésvonalán kell lenniük (2. b. ábra).
A további csúcsok ezenkívül az

A

C

D

csúcsokkal is akkora térfogatú gúlát alkotnak, mint

A B C D

, vagy az

A C D

síkban vannak. Az előbbi esetben viszont annak a két az

A C D

síkkal párhuzamos síknak egyikében vannak, amelyek olyan távolságra vannak az

A C D

síktól, mint a

B

csúcs. Ezek a síkok

S

-t egy a

D

-n átmenő

e_{0}

és a két oldalán egy-egy vele párhuzamos

e_{1}

és

e_{2}

egyenesben metszik. Ezek párhuzamosak

A C

-vel,

d

-ből két az

A B

-vel egyenlő szakaszt metszenek ki. Tekintetbe véve még azt is, hogy a további csúcsok

B C D

-vel is akkora térfogatú gúlát alkotnak, mint

A B C D

, vagy a

B C D

síkban vannak,

S

-ben egy

D

-n átmenő,

B C

-vel párhuzamos

f_{0}

egyenest és a két oldalán egy-egy vele párhuzamos

f_{1}

és

f_{2}

egyenest kapunk, amelyek távolsága

f_{0}

-tól akkora, mint az

A

csúcsé

B C

-től.
A

d

egyenes azon pontjai lehetnek csúcsai a poliédernek, amelyeken egy

e_{i}

és egy

f_{j}

egyenes is átmegy. Az ilyen pontok az

e_{0}

egyenes

E

metszéspontja és

f_{0}

-nak az

F

metszéspontja. Ugyanis a

D E F

háromszög egybevágó

C A B

-vel, mert oldalaik ellentétes irányban párhuzamosak, és

D

-ből, ill.

C

-ből húzott magasságaik egyenlők. Ha a két pont egyikét vesszük csak hozzá

A

B

C

D

-hez, akkor keletkezik egy paralelogramma-lap, mi pedig most csak háromszögekkel határolt poliédert keresünk.
Az

A B C E F D

poliédert csupa háromszöglap határolja, úgy származtatható pl. az

A B C F D

paralelogramma-alapú gúlából, hogy azt az alaplap középpontjára tükrözzük. Nevezzük röviden kettős gúlának. Ez megfelel a feladat követelményeinek, mert akárhogy választunk ki négy csúcsot, az

A

E

, a

B

F

és a

C

D

szemben fekvő csúcspárok egyike köztük van, mondjuk

B

és

F

(2. c. ábra), és ehhez az

A C E D

paralelogramma két szomszédos csúcsát kell vennünk, ha nem egy síkban levő pontnégyest akarunk kiválasztani. Az így kapott háromoldalú gúla térfogata a kettős gúla térfogatának negyedrésze.
2. Keressünk most a követelményeket kielégítő olyan poliédereket, amelyeknek van háromnál több oldalú határlapja. Legyen

A

B

C

egy ilyen lap három egymás utáni csúcsa. Egy a síkjukban fekvő további csúcsnak rajta kell lennie az

A

-n átmenő,

B C

-vel párhuzamos egyenesen, mert egyrészt a határlap konvex, így csúcsai

B C

-nek azon az oldalán vannak, amelyiken

A

, másrészt

A

-val egyenlő távolságra is vannak

B C

-től, mert különben volna két különböző területű háromszög az

A B C

síkban, és ezek egy a síkon kívül fekvő csúccsal különböző térfogatú gúlákat határoznának meg. Ugyanígy adódik, hogy a

C

-n átmenő,

A B

-vel párhuzamos egyenesen is rajta kell lennie minden további csúcsnak (3. b. ábra), tehát csak ezek

D

metszéspontja lehet még csúcsa a határlapnak, és erre az

A C D

háromszög területe is egyenlő az

A B C

-ével. Meggondolásunk azt is mutatja, hogy egy a feladat követelményeinek megfelelő poliéder minden határlapja vagy háromszög, vagy paralelogramma.

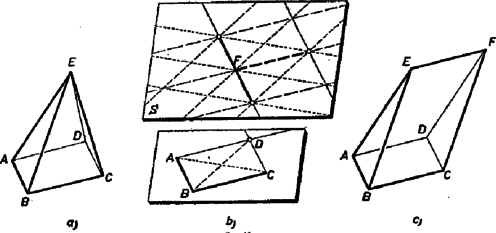3. ábra

Legyen az

A B

élen átmenő,

A B C D

-től különböző határlap egy további csúcsa

E

. Az

A B C D E

paralelogramma-alapú gúla (3. a. ábra) megfelel a feladat követelményeinek, mert belőle háromoldalú gúla csak az alaplap valamelyik csúcsának elhagyásával keletkezik, és ezeknek a térfogata mindig a négyoldalú gúla térfogatának a fele.
Ha a testnek

5

-nél több csúcsa van, akkor hasonlóan okoskodhatunk tovább, mint a csak háromszögekkel határolt poliéderek esetében. A további csúcsok csak az

E

-n^{$^{*}$} átmenő, az

A B C

síkkal párhuzamos

S

síkban lehetnek; továbbá ahhoz, hogy az

A B C D

lap valamelyik három csúcsával alkotott gúlák egyenlő térfogatúak legyenek, benne kell lenniük a

C D

élen átmenő, az

A B E

síkkal párhuzamos síkban, vagy lehetnek az

A B E

síkban. Ezek a síkok

S

-ből két az

A B

-vel párhuzamos egyenest metszenek ki (a 3. b. ábra folytonos vonallal kihúzott egyenesei). Az

A

D

E

, a

B

D

E

és az

A

C

E

csúcsokat tartalmazó csúcsnégyeseket is figyelembe véve három egyeneshármas adódik, ‐ az előző meggondolás

e_{0}

e_{1}

e_{2}

és

f_{0}

f_{1}

f_{2}

egyeneseinek megfelelően, melyek rendre

A D

-vel,

B D

-vel, ill.

A C

-vel párhuzamosak (a 3. b. ábra hosszú szaggatott vonallal, apró szaggatott vonallal, ill. pontozva jelölt egyenesei). A további esetleges csúcsoknak mindegyik egyeneshármas valamelyik egyenesén rajta kell lennie.

Így azok a pontok jönnek tekintetbe poliédercsúcsokként, amelyeken négy különféleképpen jelölt egyenes megy át. Könnyen belátható, hogy ezek az egyenesek az

S

síkban

A B C D

-vel egybevágó paralelogrammákat, ezek átlóit és egyes csúcsokon átmenő, átlókkal párhuzamos egyeneseket alkotnak. Három olyan pont keletkezik, amelyiken mind a négy féle egyenesből megy át egy-egy; kettőbe

E

-ből az

A B

éllel párhuzamos, egyenlő hosszú, és egyező, ill. ellentétes irányú szakasz vezet, egybe pedig

A D

-vel párhuzamos, egyenlő hosszú és egyirányú szakasz. Az első két pontból csak az egyik tartozhatik a poliéderhez. Ha a poliéderen a három pont közül csak az egyik lesz csúcs, akkor háromoldalú hasábot kapunk (3. c. ábra), és minden háromoldalú hasáb megfelel a feladat követelményeinek. Ha ugyanis kiválasztunk négy csúcsot, akkor a paralelogramma lapok három közös éle közül valamelyiknek mind a két végpontja ki van választva, minden további csúcs ezek valamelyikével valamelyik paralelogramma-lapon szomszédos, tehát mindig ki van választva valamelyik paralelogramma-lap három csúcsa, és ha a négy csúcs nincs egy síkban, akkor a negyedik csúcs a paralelogrammához nem tartozó él egyik végpontja. Minden ilyen háromoldalú gúla térfogata a hasáb térfogatának harmadrésze.

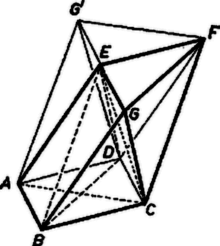4. ábra

Megmutatjuk végül, hogy a három pont közül nem lehet kettő egyszerre csúcsa a poliédernek. Ha ugyanis az

E

-től

A D

irányban levő

F

pont is, az

A B

irányban levő

G

pont is csúcsa a poliédernek (4. ábra), akkor a

C F G

síkkal párhuzamos síkban vannak az

E

B

D

csúcsok (a két csúcshármas alkotta háromszög megfelelő oldalai párhuzamosak),

A

pedig nincs egyik síkban sem, tehát pl. az

A C F G

és

B C F G

gúlák különböző térfogatúak. Ha

G

helyett az

E

-re vonatkozó

G'

tükörképe csúcsa a poliédernek, akkor az

A D

és

B C

él szerepe cserélődik meg, a

D F G'

és

E A C

síkok párhuzamosak, és

B

nincs egyikben sem. Így pl. a

B D F G'

és

A D F G'

gúlák térfogata különböző.
A feladat követelményeinek tehát a paralelogramma-alapú gúlák, a négyoldalú kettős gúlák és a háromoldalú hasábok felelnek meg, ide számíthatók továbbá a háromoldalú gúlák.

II. megoldás. 1. Keressük sorra a követelményeket kielégítő 4-, 5-, 6- stb. csúcsú poliédereket. Egy négy csúcsú poliéder csak háromoldalú gúla lehet és az megfelelőnek tekinthető.
2. Legyen

A B C D E

egy a követelményeknek megfelelő öt csúcsú poliéder, és

A

B

C

D

ennek négy nem egy síkban levő csúcsa. A konvexség miatt

E

nem lehet az

A B C D

gúla belsejében vagy határán, így valamelyik három csúcsán átmenő síknak ellenkező oldalán van, mint a gúla negyedik csúcsa; legyen ez az

A B C

sík. A

D E

szakasz

A B C

síkkal való

E_{1}

metszéspontja felezi a

D E

szakaszt, mert az

A B C D

és

A B C E

gúla térfogata egyenlő, így

E

ugyanakkora távolságra van az

A B C

síktól, mint

D

(5. a. ábra).

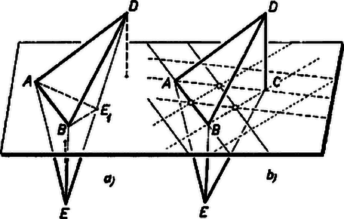5. ábra

Vagy benne van

E

A B D

síkban, vagy az

A B D E

és

A B C D

gúlák térfogata egyenlő. Utóbbi esetben bontsuk

A B D E

-t az

A B E_{1} D

és

A B E_{1} E

gúlákra. Ezeknek a közös lapjukra bocsátott magassága egyenlő, és egyenlő az

A B C D

gúla

D

-ből húzott testmagasságával. Így az

A B E_{1}

háromszög területe fele akkora, mint az

A B C

háromszögé.

E_{1}

tehát vagy az

A B

oldalon van, vagy azoknak az

A B

-vel párhuzamos egyeneseknek az egyikén, amelyek fele akkora távolságra vannak tőle, mint a

C

csúcs (5. b. ábra). Hasonlóan rajta kell lennie

E_{1}

-nek a

B C

oldalon, vagy annak a két vele párhuzamos egyenesnek az egyikén, amelyek

B C

-től félakkora távolságra vannak, mint az

A

csúcs; ugyancsak teljesülnie kell az

A C

oldalra vonatkozó megfelelő feltételnek is. Mindhárom oldallal párhuzamos egyenes csak az

A B

B C

C A

oldalak felezőpontjain megy át. Ezek bármelyikére is tükrözzük

D

-t, paralelogramma-alapú gúlát kapunk, és az

E

pont keresése közben már biztosítottuk, hogy az ebből kiválasztható bármelyik háromoldalú gúlának ugyanakkora legyen a térfogata.
3. Ha kiválasztjuk egy hat csúcsú, a követelményeknek megfelelő poliéder öt nem egy síkban levő csúcsát, ezek is a követelményeknek megfelelő poliédert határoznak meg, mert minden a csúcsai közül kiválasztható pontnégyes az eredeti poliéder csúcsai közül is kiválasztható, tehát bármely négy csúcs, ha nincs egy síkban, ugyanakkora térfogatú háromoldalú gúlát határoz meg.
Eszerint, ha az

A B C D E F

poliéder teljesíti a követelményeket, akkor az itt nem egy síkban levő csúcs meghatározta:

A B C D E

poliéder is, tehát, mint éppen láttuk, paralelogramma-alapú gúlának kell lennie. Az

F

csúcs vagy a gúla valamelyik háromszöglapjának, vagy a paralelogramma-lapnak ellenkező oldalán van, mint a többi csúcs.
Legyen

B C D E

a paralelogramma-lap, és

F

A B C

lap ellenkező oldalán, mint a gúla. Az öt csúcsú testnél követett meggondolást egyrészt az

A B C D

gúlára és az

F

csúcsra, másrészt az

A B C E

gúlára és az

F

csúcsra alkalmazva azt nyerjük, hogy

F

D

csúcsból is, és

E

-ből is az

A B

B C

C A

élek egyikének a felezőpontjára való tükrözéssel áll elő. A hat tükörkép közül csak

E

-nek

A B

felezőpontjára és

D

-nek

A C

felezőpontjára vonatkozó tükörképe esik egybe, ez lehet tehát csak az

F

csúcs. Ez a

A E D C F B

háromoldalú hasáb (6. ábra).

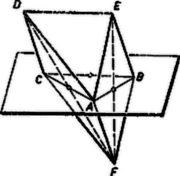6. ábra

A háromoldalú hasáb valóban ki is elégíti a követelményeket. Ezt tudjuk már az

A B C D E

gúlára és az

F B C D E

négyoldalú gúlából kiválasztható háromoldalú gúlák térfogata ugyanakkora, mint az

A B C D E

-ből kiválaszthatóké, mert a két négyoldalú gúla egyenlő térfogatú, ugyanis

A

és

F

távolsága a

B C D E

paralelogramma síkjától ugyanakkora. Végül az

F

pont választása szerint az

A D C F B

, ill. az

A E B F C

poliéderből kiválasztható háromoldalú gúlák is egyenlő térfogatúak, és térfogatuk egyenlő az

A B C D

, ill. az

A B C E

gúla térfogatával, amik az

A B C D E

gúlának is részei. Így az összes kiválasztható háromoldalú gúlák egyenlő térfogatúak.
4. Keressük most az olyan

A B C D E F

poliédereket, amelyekben

F

A B C D E

gúla

B C D E

paralelogramma-lapjának van ellenkező oldalán, mint a gúla. Ezekre az

A F

szakasznak a

B C D E

síkba eső

F_{1}

felezőpontja az előzőkhöz hasonlóan vagy a

B C

egyenesen van, vagy attól félakkora távolságra, mint a

D E

egyenes; de ugyanakkor

F_{1}

vagy rajta van

D E

-n, vagy félakkora távolságra van tőle, mint

B C

. A két feltételt egyszerre a paralelogramma

B C

-vel párhuzamos középvonalának pontjai elégítik ki (7. ábra).

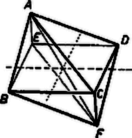7. ábra

Ugyanígy rajta kell lennie

F_{1}

-nek a

C D

-vel párhuzamos középvonalon is: Így

F_{1}

a paralelogramma középpontja,

F

A

csúcs erre vonatkozó tükörképe, a poliéder kettős paralelogramma-alapú gúla.
Ez a test valóban kielégíti a feladat követelményeit, mert az

A B C D E

gúlára ezt már tudjuk,

F

megkeresése pedig biztosította, hogy a kiválasztható,

F

-et és

A

-t tartalmazó háromoldalú gúlák térfogata egyenlő pl.

A B C D

-ével, továbbá ekkora az

F B C D E

poliéderből kiválasztható háromoldalú gúlák térfogata is, hiszen ez a poliéder az

A B C D E

poliéder tükörképe. Végül

A

-t is,

F

-et is elhagyva, egy síkban levő négy pont marad.
5. Megmutatjuk, hogy hatnál több csúcsú test nem elégíti ki a követelményeket. Ha kielégítené, akkor minden

7

csúcsú rész-teste is kielégítené a követelményeket. Egy ilyen

7

csúcsú testből

6

nem egy síkban levő csúcs az előzőek szerint vagy háromoldalú hasábot, vagy négyoldalú kettős gúlát határoz meg. Utóbbi esetben a hetedik

G

csúcs a test egy

L

lapjának ellenkező oldalán van, mint maga a test. De a kettős gúlának határlapja

L

-nek a test középpontjára vonatkozó

L'

tükörképe is, ami párhuzamos

L

-lel. Ekkor azonban két különböző térfogatú háromoldalú gúlát kapunk, ha

L'

-höz egyszer

G

-t, egyszer pedig

L

-nek valamelyik csúcsát vesszük.
Ha

6

csúcsot kiválasztva ezek háromoldalú hasábot határoznak meg, akkor a hetedik

G

csúcs ismét valamelyik határlapnak ellenkező oldalán van, mint a hasáb többi csúcsa. Az utolsó meggondolás mintájára látható, hogy

G

nem lehet az egyik háromszöglap ellenkező oldalán, mint a hasáb. Ha viszont

G

egy paralelogramma-lapnak van ellenkező oldalán, mint a hasáb, akkor a 4. pont meggondolását a paralelogramma és a további két csúcs egyike, ill. a másika alkotta gúlára alkalmazva azt kapjuk, hogy

G

mindkét csúcsnak tükörképe kellene hogy legyen a paralelogramma középpontjára, ez a két tükörkép azonban különböző. Így hasábhoz sem található hetedik csúcs.
Azt nyertük tehát, hogy a feladat követelményeinek a paralelogramma-alapú gúlák, a négyoldalú kettős gúlák, és a háromoldalú hasábok felelnek meg, amikhez még hozzávehetjük a háromoldalú gúlákat is, más poliédert nem.

Surányi János

^{$^{*}$}A 3. b ábrán

F

javítandó

E

-re.