Kezdőlap


Cím:	Az 1964. évi Országos Középiskolai Matematikai Tanulmányi Verseny I. fordulóján kitűzött feladatok megoldása
Szerző(k):	Lukács Ottó , Scharnitzky Viktor
Füzet:	1964/november, 97 - 104. oldal	PDF \| MathML
Témakör(ök):	OKTV

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

1. feladat. Az $A B C$ háromszög $A B$ és $A C$ oldalai fölé (kifelé) az $A C_{1} C_{2} B$ és $A B_{1} B_{2} C$ négyzeteket rajzoljuk. Bizonyítandó, hogy a $B_{2} C_{2}$ szakasz felezőpontja a $B C$ átmérőjű körön fekszik:

I. megoldás. Szorítkozzunk egyelőre arra az esetre, amikor

B_{2}

és

C_{2}

B C

egyenesnek ugyanazon az oldalán van, vagyis amikor a háromszög

B

-nél és

C

-nél levő szöge hegyesszög.
Vetítsük az

A

B_{2}

C_{2}

pontokat és a

C_{2} B_{2}

szakasz

F

felezőpontját a

B C

egyenesre, legyenek vetületeik rendre

A^{*}

B_{2}^{*}

C_{2}^{*}

és

F^{*}

(1. ábra). Minthogy a négyzeteket kifelé szerkesztettük,

B_{2}^{*}

ill.

C_{2}^{*}

B C

szakasz

C

-n, ill.

B

-n túli meghosszabbításán van.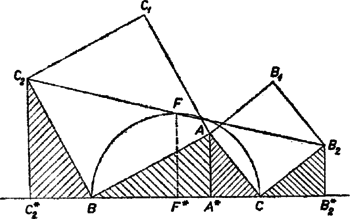

1. ábra

C_{2} C_{2}^{*} B

és

B A^{*} A

derékszögű háromszögek egybevágók, mert

C_{2} B = B A

, és

C_{2}^{*} C_{2} B ∢ = A^{*} B A ∢

merőleges szárú hegyesszögek. Hasonlóan az

A A^{*} C

és

C B_{2}^{*} B_{2}

derékszögű háromszögek is egybevágók. Ezekből következik, hogy a

C_{2} C_{2}^{*} B_{2}^{*} B_{2}

trapéz két párhuzamos oldalának összege

\begin{matrix} C_{2} C_{2}^{*} + B_{2} B_{2}^{*} = B A^{*} + A^{*} C = B C, \end{matrix}

és így a trapéz középvonalának hossza

\begin{matrix} F F^{*} = \frac{B C}{2}, \end{matrix}

továbbá ez a középvonal merőleges

B C

-re. Ez azt jelenti, hogy

F

B C

egyenes

F^{*}

pontjától és egyszersmind magától az egyenestől is

B C / 2

távolságra van.
Bebizonyítjuk még, hogy

F^{*}

B C

szakasz felezőpontja. Ezekből már következik, hogy

F

rajta van a

B C

fölé, mint átmérő fölé rajzolt körön, mégpedig a

B C

-re merőleges átmérő egyik végpontja

F

F^{*}

egyrészt felezi a

C_{2}^{*} B_{2}^{*}

szakaszt, másrészt az

F^{*} C

szakasz ugyanannyival kisebb

F^{*} B_{2}^{*}

-nál, mint

B F^{*}

C_{2}^{*} F^{*}

-nál, tudniillik ‐ a fenti egybevágóságok szerint ‐

A A^{*}

-gal. Így

F^{*}

valóban felezi a

B C

szakaszt. Ezzel a bizonyítást ‐ a tett megszorító feltétel teljesülése esetére ‐ befejeztük.

Ha az

A B C

háromszögben a

B

-nél és

C

-nél levő szögek valamelyike, mondjuk a

C

-nél levő, derékszög, akkor egyszerűbb helyzettel állunk szemben, mert

B_{2}

B C

egyenesen adódik, és a

C_{2} C_{2}^{*} B_{2}^{*} B_{2}

trapéz szerepét a

C_{2} C_{2}^{*} B_{2}

derékszögű háromszög veszi át; a bizonyítás ennek megfelelő, kézenfekvő egyszerűsítésekkel ebben az esetben is alkalmazható.
Ha pedig, mondjuk

C

-nél, tompaszög van, akkor a

B_{2} C_{2}

és

B_{2}^{*} C_{2}^{*}

szakaszok metszik egymást, a

C_{2} C_{2}^{*} B_{2} B_{2}^{*}

trapéz átlói lesznek (2. ábra),

F F^{*}

az ezek felezőpontjait összekötő szakasz. Ez ‐ mint könnyen bebizonyítható ‐ minden konvex trapézban egyenlő a párhuzamos oldalak különbségének felével, az utóbbiról pedig a hegyesszögű esetben alkalmazott gondolatmenettel belátható, hogy egyenlő a

B C

szakasznak a felével. Ezek szerint az állítás minden háromszögre érvényes.

2. ábra

Megjegyzés. A fenti megoldáshoz hasonló gondolatmenettel ‐ alkalmas koordinátarendszert választva ‐ egyszerű analitikus geometriai megoldás is adható.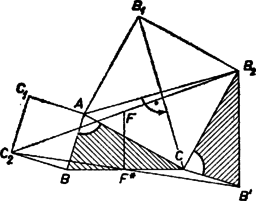

II. megoldás. Forgassuk el az

A B C

háromszöget az

A C B_{2} B_{1}

négyzet középpontja körül

90^{\circ}

-kal úgy, hogy

A

C

-be kerüljön. Így

C

B_{2}

-be kerül,

B

elforgatott helyzete pedig legyen

B'

(3. ábra). Ekkor

B' C

merőleges

B A

-ra és egyenlő vele, tehát párhuzamos, egyenlő és egyező irányítású

B C_{2}

-vel. Így

B

C_{2}

C

B'

ebben a sorrendben paralelogrammát határoznak meg, tehát a

B C

átló

F^{*}

felezőpontja a

C_{2} B'

átlót is felezi.

3. ábra

A végzett forgatás folytán

B' B_{2}

merőleges

B C

-re és egyenlő vele. Most már az

F F^{*}

szakasz a

C_{2} B_{2} B'

háromszög középvonala, tehát egyenlő a

B' B_{2}

és

B C

szakaszok felével. Ezek szerint

B

C

és

F

egyenlő távolságra vannak

F^{*}

-tól, ez pedig azt jelenti, hogy

F

B C

átmérő fölé rajzolt körön van.
Ez a bizonyítás tetszés szerinti alakú

A B C

háromszög esetén érvényes.

III. megoldás. Forgassuk el az

A B C

háromszöget előbb

B

körül

90^{\circ}

-kal úgy, hogy

A

C_{2}

-be jusson, majd

C

körül

90^{\circ}

-kal úgy, hogy

A

B_{2}

-be jusson, legyen az első esetben

C

új helyzete

C_{0}

, a második esetben

B

új helyzete

B_{0}

(4. ábra). A két forgatás ellentétes irányú, a négyzetek kifelé való szerkesztése miatt. A két forgatási szög összege

180^{\circ}

, ezért

B C_{2}

és

B_{0} B_{2}

párhuzamosak és ellentétes irányúak. Továbbá egyenlőek is, és ezért a

B C_{2} B_{0} B_{2}

négyszög paralelogramma. Így a

C_{2} B_{2}

átló kérdéses

F

felezőpontja a

B B_{0}

átlót is felezi.
Másrészt a forgatásokból következik, hogy a

B C_{0} B_{0} C

négyszög négyzet, tehát az átlók közös

F

felezőpontjából az oldalak derékszögben látszanak, így

F

B C

oldal, mint átmérő fölé rajzolt Thales-körön van, éppen a

B C

-re merőleges átmérő egyik végpontja.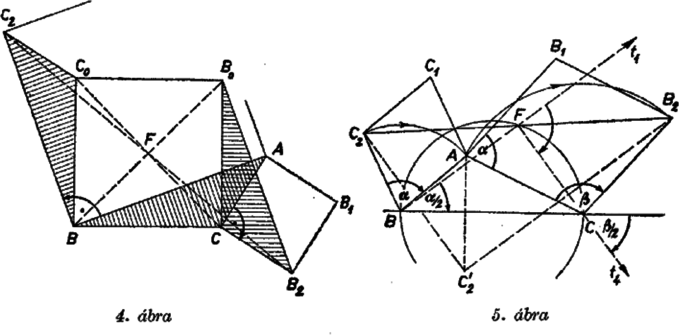

IV. megoldás. A

C_{2}

pontot átvihetjük

B_{2}

-be úgy, hogy elforgatjuk először

B

körül

α = 90^{\circ}

-kal, ‐ így

A

-ba kerül ‐, majd

A

-t elforgatjuk

C

körül ugyanabban az irányban

β = 90^{\circ}

-kal (5. ábra).
Ismeretes, hogy egy (síkbeli) forgatás helyettesíthető bármely két olyan egymás utáni tükrözéssel, amelyek tengelye átmegy a forgatás középpontján, és az első tengelyt a második tengelybe átvivő forgatás fele akkora szögű, mint az eredeti forgatás, és azzal megegyező irányú.
Helyettesítsük a mondott forgatásokat két-két tükrözéssel úgy, hogy ezek

t_{1}

t_{2}

és

t_{3}

t_{4}

tengelypárja közül

t_{2}

és

t_{3}

azonos legyen. Így ugyanis a harmadik tükrözés visszaállítja a második tükrözés előtti helyzetet, és a négy tükrözés kettőre csökkenthető. Mivel

t_{2}

nek

B

-n,

t_{3}

-nak

C

-n kell átmennie, így mindkettőnek egyaránt a

B C

egyenest kell választanunk. Ilyen választás mellett

C_{2}

-t a

B

-n áthaladó és

B C

-vel

α / 2

szöget bezáró

t_{1}

, majd a

C

-n átmenő és

B C

-vel

β / 2

szöget bezáró

t_{4}

tengelyen való tükrözés viszi át

B_{2}

-be.
Ez a két tükrözés ‐ az idézett tétel megfordítása alapján ‐ helyettesíthető egyetlen forgatással, amelynek középpontja a

t_{1}

és

t_{4}

metszéspontja, szöge kétszer akkora, mint a

t_{1}

-et

t_{4}

-be átvivő forgatás, és iránya megegyezik az utóbbi forgatás irányával. A két tengely szöge (mint a

t_{1}

t_{2}

és

t_{4}

határolta háromszög külső szöge)

\begin{matrix} \frac{α}{2} + \frac{β}{2} = 90^{\circ}, \end{matrix}

(1)

így

C_{2}

-t a

B_{2}

-be

180^{\circ}

-os forgatás viszi át, vagyis a tengelyek metszéspontja éppen a

B_{2} C_{2}

szakasz

F

felezőpontja.
Mivel pedig az

F

pontból a

B C

szakasz

90^{\circ}

-os szögben látszik, azért

F

rajta van a

B C

átmérőjű Thales-körön, ezt kellett bizonyítanunk.

Megjegyzés. A bizonyításban

α

-ról és

β

-ról csak azt használtuk fel (1)-ben, hogy összegük

180^{\circ}

. A feladat állítása tehát helyes marad akkor is, ha a háromszög

A B

és

A C

oldalára kifelé olyan rombuszokat rajzolunk, melyeknek

B

-nél, ill.

A

-nál levő szöge egyenlő; továbbá akkor is, ha mindkét oldalra befelé rajzoljuk a rombuszokat. Az általánosított állítás bizonyítható ‐ értelemszerű módosításokkal a II. és III. megoldás gondolatmenetével is.

2. feladat. Mennyi a

K = 5 x - 6 y + 7 z

kifejezés legkisebb és mennyi a legnagyobb értéke, ha

x

y

és

z

olyan nem negatív számok, melyekre fennáll

\begin{matrix} 4 x + y + 2 z = 4 \end{matrix}

(2)

és

\begin{matrix} 3 x + 6 y - 2 z = 6 ? \end{matrix}

(3)

I. megoldás. Fejezzük ki a három paramétertől függő

K

kifejezést egyetlen paraméterrel, pl.

x

-szel. A feltételi egyenletekből összeadással és rendezéssel

\begin{matrix} y = \frac{10}{7} - x, \end{matrix}

(4)

és ezt felhasználva pl. (2)-ből

\begin{matrix} z = \frac{9}{7} - \frac{3}{2} x . \end{matrix}

(5)

A feltétel alapján

x

nem lehet negatív, a

0

értéket azonban már felveheti, mert

x = 0

esetén (4) és (5) szerint

y

és

z

pozitívok,

x

minimális értéke tehát

0

. Másrészt abból, hogy

y

és

z

nem negatív,

x

-re (4) és (5) alapján

\begin{matrix} x \leq \frac{10}{7}, illetve x \leq \frac{6}{7} \end{matrix}

adódik, tehát

x

maximális értéke

\frac{6}{7}

.
(4) és (5) felhasználásával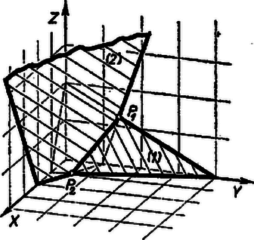

\begin{matrix} K = 5 x - 6 y + 7 z = \frac{x}{2} + \frac{3}{7}, \end{matrix}

ennek értéke

x

növekedésével nő, tehát legkisebb és legnagyobb értéke ‐ az

x

minimális és maximális értékét behelyettesítve ‐

\begin{matrix} K_{{min}_{}^{}} = \frac{3}{7}, illetve K_{{max}_{}^{}} = \frac{6}{7} . \end{matrix}

6. ábra

II. megoldás. Szemléltessük a feladatban szereplő háromváltozós kifejezéseket egy térbeli derékszögű koordinátarendszerben. (A térbeli koordináta geometria bizonyos elemeinek ismeretét ebben a megoldásban feltételezzük.)
A (2) és (3) egyenletek egy-egy síkot határoznak meg a térben (6. ábra). A mind a két egyenletet kielégítő számhármasok az e két sík metszésvonalán elhelyezkedő pontok koordinátái. Az

x \geq 0

y \geq 0

z \geq 0

további feltételek miatt ennek a metszésvonalnak csak az első térnyolcadba (és annak határára) eső része jön szóba, ez pedig a

P_{1} (0, 10 / 7, 9 / 7)

ponttól a

P_{2} (6 / 7, 4 / 7, 0)

pontig terjed.
Az

5 x - 6 y + 7 z = K

egyenlet minden adott

K

értékre egy-egy síkot határoz meg, amely az

X

Y

Z

- tengelyből rendre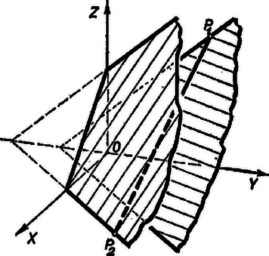

\begin{matrix} a = K / 5, b = - K / 6, c = K / 7 \end{matrix}

hosszúságú szakaszt metsz le. Ezek egyenes arányban vannak

K

-val, tehát a különböző

K

értékekhez tartozó síkoknak a koordináta-síkokba eső metszésvonalai párhuzamosak, így maguk a síkok is párhuzamosak.

7. ábra

Ábrázoljuk a párhuzamos síksereg

P_{1}

-en, illetve

P_{2}

-n átmenő egyedét (7. ábra).

K

értéke

P_{1}

-ben

3 / 7

P_{2}

-ben

6 / 7

, különbözők, így

P_{1}

-en és

P_{2}

-n a síksereg két különböző egyede halad át, a tengelymetszetek

\begin{matrix} a_{1} = 3 / 35, & b_{1} = - 3 / 42, & c_{1} = 3 / 49, & illetve \\ a_{2} = 6 / 35, & b_{2} = - 6 / 42, & c_{2} = 6 / 49. \end{matrix}

P_{1} P_{2}

szakasz minden egyes belső pontján a párhuzamos síkseregnek egy és csak egy ‐ a két megrajzolt sík közti ‐ egyede megy át. A tengelymetszetekből megállapítható, hogy

P_{1}

-től

P_{2}

felé haladva

K

értéke növekszik, tehát a fenti

K_{1}

a legkisebb,

K_{2}

a legnagyobb érték.

3. feladat. Az

A B C

hegyesszögű háromszög

B

és

C

csúcsában az

A B

, illetőleg

A C

oldalra emelt merőlegesek metszéspontja

P

P

-nek a

B C

szakaszon levő (merőleges) vetülete

Q

. Bizonyítandó, hogy a

Q

ponton átmenő,

B C

-től különböző egyeneseknek a

B A C

szög szárai közé eső szakasza nagyobb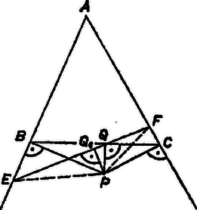

B C

-nél.

I. megoldás. Legyen egy a

Q

ponton áthaladó, a

B C

-től különböző egyenesnek az

A B

szárral való metszéspontja

E

A C

-vel való metszéspontja

F

(8. ábra). A

P

-ből az

E F

-re húzott merőleges talppontja legyen

Q_{1}

8. ábra

Hasonlítsuk össze (Pythagoras tétele alapján) a

B Q

és

E Q_{1}

, továbbá a

Q C

és

Q_{1} F

szakaszokat. A

B P Q

és

E P Q_{1}

derékszögű háromszögekből

\begin{matrix} B Q = \sqrt[]{B P^{2} - P Q^{2}}, E Q_{1} = \sqrt[]{E P^{2} - P Q_{1}^{2}} . \end{matrix}

P Q Q_{1}

és

P E B

derékszögű háromszögekből nyilvánvalóan

\begin{matrix} P Q > P Q_{1} \end{matrix}

(6)

\begin{matrix} és E P > B P . \end{matrix}

(7)

Ezek szerint

B Q

kifejezésében a kisebbítendő kisebb, a kivonandó pedig nagyobb, mint

E Q_{1}

kifejezésében, tehát

\begin{matrix} B Q < E Q_{1} . \end{matrix}

(8)

Ugyanígy a

P F C

derékszögű háromszögből adódó

\begin{matrix} P F > P C \end{matrix}

(9)

felhasználásával a

C P Q

F P Q_{1}

és

P Q Q_{1}

derékszögű háromszögekből

\begin{matrix} Q C = \sqrt[]{P C^{2} - P Q^{2}} < \sqrt[]{P F^{2} - P Q^{2}} < \sqrt[]{P F^{2} - P Q_{1}^{2}} = Q_{1} F . \end{matrix}

(10)

Megmutatjuk még, hogy

Q

B C

szakaszon,

Q_{1}

E F

szakaszon van. Ekkor (8)-at és (10)-et összeadva következik a bizonyítandó egyenlőtlenség:

\begin{matrix} B C = B Q + Q C < E Q_{1} + Q_{1} F = E F . \end{matrix}

(11)

Q

és

Q_{1}

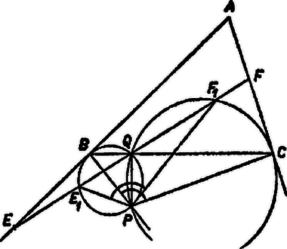
helyzetére kimondott állítás így látható be. Az

A B C

háromszög

B

-nél és

C

-nél levő szöge hegyesszög, így az

A B

-re

B

-ben és

A C

-re

C

-ben állított merőlegeseknek az oldalegyenesektől a háromszöget tartalmazó félsíkba induló félegyenesei

B C

-vel hegyesszöget zárnak be. Így

P

ezeknek a félegyeneseknek a metszéspontja, vetülete,

Q

, a

B C

szakaszon van, és

P

B C

egyenes ellenkező oldalán fekszik, mint

A

.
Ha

E

A B

oldal

B

-n túli meghosszabbításán van ‐ amit a továbbiakban mindig felteszünk, mert, ha kell, a betűzés megcserélésével elérhetünk ‐, akkor

E

és

P

B C

egyenes ugyanazon oldalán van, tehát

B E P Q

konvex négyszög;

E

-nél levő szöge, mint a

B E P

derékszögű háromszög egyik szöge, hegyesszög,

Q

-nál levő szöge pedig derékszög, tehát az

E Q

átló

P E

-vel is,

P Q

-val is hegyesszöget zár be, s így

Q_{1}

E Q

szakasz belső pontja. Ezzel a bizonyítást befejeztük.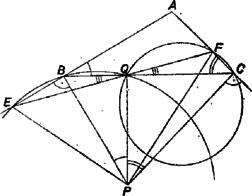

Megjegyzés. A feladat állítása érvényes, akármekkora is a háromszög

A

-nál levő szöge, hiszen csak a

B

és

C

csúcsnál levő szögről használtuk fel, hogy hegyesszögek. Világos, hogy érvényes marad akkor is, ha pl.

B

-nél derékszög van, ekkor ugyanis

P

és

Q

egybeesik

C

-vel. Ha viszont pl.

B

-nél tompaszög van, akkor a (11) egyenlőtlenség nem következik (8)-ból és (9)-ből, mert az utolsó két bekezdés meggondolásai nem érvényesek,

Q

B C

szakaszon kívül keletkezik, és valóban

E F

lehet kisebb is, nagyobb is, mint

B C

II. megoldás. Az I. megoldás (7) és (9) egyenlőtlensége szerint az

E P F

háromszögben a

P

-ből induló oldalak nagyobbak, mint a

B P C

háromszög megfelelő oldalai. Megmutatjuk, hogy egyrészt

E P F ∢ > B P C ∢

, másrészt hogy ebből, továbbá a

B C P

és

C B P

szögek hegyesszög voltából következik, hogy a harmadik oldal is az

E P F

háromszögben nagyobb.

9. ábra

A szögekre kimondott egyenlőtlenség igazolására rajzoljuk meg a

B

E

Q

, valamint a

C

F

Q

pontokon áthaladó köröket (9. ábra).

P

az első kör belsejében van, mert a

B Q

szakasz

P

-ből az

A B C

szöggel egyenlő szög alatt látszik (merőleges szárú hegyesszögek),

E

-ből pedig ennél kisebb szög alatt. A másik körön viszont kívül fekszik

P

, mert a

Q F C

ív

P

-ből vett látószöge akkora, mint az

A C B

szög, a

P

-vel egy oldalon levő kiegészítő ív pontjaiból vett látószög pedig nagyobb, mert innen a

Q F

rész-ív látható ekkora szög alatt. Ezek alapján

\begin{matrix} E P B ∢ > E Q B ∢ = F Q C ∢ > F P C ∢, \end{matrix}

és a két szélső szöghöz a

B P F

szöget hozzáadva valóban

\begin{matrix} E P F ∢ > B P C ∢ . \end{matrix}

(12)

10. ábra

E P F

és

B P C

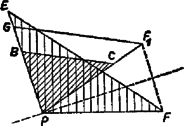háromszögek

E F

és

B C

oldalaira vonatkozó állítás igazolásához úgy forgattuk el a

B P C

háromszöget

P

körül, hogy

B

P E

szakaszra essék (10. ábra), a

P C

-nél hosszabb

P F

oldalt pedig

P

-től rámértük a

P C

félegyenesre is, a végpont

F_{1}

. Húzzunk most

B C

-vel párhuzamost

E

és

F_{1}

közül azon a ponton át, amelyik közelebb van

B C

-hez (a 10. ábrán az

F_{1}

pont az), messe a párhuzamos

P E

-t

G

-ben. Mivel

P C < P F = P F_{1}

, azért nyilvánvalóan

\begin{matrix} B C < G F_{1} . \end{matrix}

(13)

Ha az

A B C

háromszög

B

-nél és

C

-nél levő szöge hegyesszög, akkor a

P B C

-vel egyenlő

P G F_{1}

szög is hegyesszög, és így kiegészítő szöge, az

E G F_{1}

szög, tompaszög. Ezért

\begin{matrix} G F_{1} < E F_{1} . \end{matrix}

Ezt (13)-mal egybevetve

\begin{matrix} B C < E F_{1} . \end{matrix}

(14)

Mivel az

E P F_{1}

és

E P F

háromszögek két-két oldala egyenlő, de közbezárt szögük az előbbi háromszögben kisebb, azért¹

\begin{matrix} E F_{1} < E F, \end{matrix}

és ezt (14)-gyel egybevetve

B C < E F

; az állítást bebizonyítottuk.

Megjegyzés: A (12) egyenlőtlenség a következőképpen is belátható. Rajzoljunk köröket a

B P

és

C P

szakaszok, mint átmérők fölé; ezek egymást

P

-ben és

Q

-ban metszik. Legyen ezek

Q

-tól különböző metszéspontja

E F

-fel

E_{1}

, illetőleg

F_{1}

(11. ábra).

P

-ből az

E_{1} F_{1}

szakasz ugyanakkora szögben látható, mint a

B C

szakasz:

E_{1} P F_{1} ∢ = B P C ∢

, mert a

B P F_{1}

szög közös részük, nem közös

E_{1} P B

, illetőleg

F_{1} P C

részük pedig egyenlő a vele egy íven nyugvó

E_{1} Q B

, illetőleg

F_{1} Q C = F Q C

szöggel, ha

F_{1}

Q F

szakaszon, vagy annak

Q

végpontjában van, ‐ az utóbbi szögek viszont csúcsszögek. Ha pedig

F_{1}

Q E

szakaszon van, akkor az

E_{1} Q B

szög külső szöge az

F_{1} P C Q

húrnégyszögnek, az

F_{1} P C

rész-szög pedig belső szög a négyszög

Q

-val szemben fekvő csúcsánál, tehát a nem közös szög-részek egyenlősége ilyenkor is fennáll.

11. ábra

E_{1} F_{1}

szakasz része az

E F

szakasznak, az

E_{1} P F_{1}

szög része az

E P F

szögnek, tehát valóban fennáll

E P F ∢ > B P C ∢

. (Bizonyítani kellene még az

E_{1}

F_{1}

pontok helyzetéről felhasznált állítást.)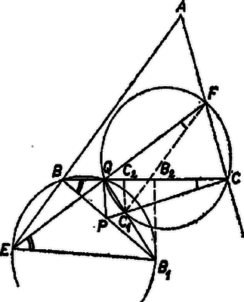

12. ábra

III. megoldás. Állítsunk merőlegest

Q

-ban

E F

-re, és messe ez a

P C

egyenest

C_{1}

-ben,

P B

-t pedig

B_{1}

-ben;

B_{1}

és

C_{1}

merőleges vetülete a

B C

egyenesen legyen

B_{2}

, ill.

C_{2}

(12. ábra).

E

A B

oldal meghosszabbításán van, ezért a merőleges a

P Q C

derékszögű szögtartományban halad, tehát a

B C P

háromszög

P C

oldalát és a

B P

oldal meghosszabbítását metszi, továbbá

C_{2}

Q C

szakaszon adódik. Ezért

Q C_{1} < Q B_{1}

, és egyszersmind

\begin{matrix} Q C_{2} < Q B_{2} . \end{matrix}

(15)

C

és

Q

rajta van a

C_{1} F

átmérő fölötti Thales-körön. A

Q F C_{1}

és

Q C C_{1}

szögek egyenlők, mint ugyanazon íven nyugvó kerületi szögek, így a

Q F C_{1}

és

C_{2} C C_{1}

derékszögű háromszögek hasonlók. A két átfogó közül

F C_{1}

a nagyobb, mert a körnek átmérője, tehát a megfelelő befogókra

\begin{matrix} F Q > C C_{2} . \end{matrix}

(16)

B C

-ből még fennmaradt

C_{2} B

szakasz helyett a nála nagyobb

B_{2} B

-ről mutatjuk meg, hogy kisebb az

E F

-ből fennmaradt

E Q

-nál. (

B_{2} B

B C

-nél nagyobb is lehet.) Ehhez a

B B_{1} B_{2}

és az

E B_{1} Q

háromszögeket hasonlítjuk össze.

B

és

Q

rajta van az

E B_{1}

átmérő fölé rajzolt Thales-körön, ezért egyrészt

\begin{matrix} E B_{1} > B B_{1}, \end{matrix}

másrészt a két háromszögben az egy íven nyugvó

B_{1} E Q

és

B_{1} B Q

kerületi hegyes szögek egyenlők. Így a két háromszög hasonló, és az

E B_{1} Q

háromszög oldalai nagyobbak, tehát

\begin{matrix} E Q > B B_{2} . \end{matrix}

(17)

Most már a (15)‐(17) egyenlőtlenségek alapján valóban

\begin{matrix} E F = E Q + Q F > B B_{2} + C_{2} C = B Q + Q B_{2} + C_{2} C > B Q + Q C_{2} + C_{2} C = B C . \end{matrix}

13. ábra

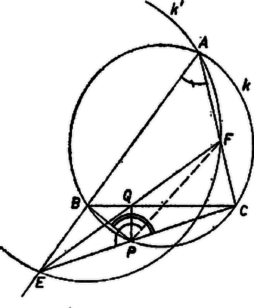IV. megoldás. A feladat állítása következik abból is, ha megmutatjuk, hogy az

A E F

háromszög köré írt

k'

kör átmérője nagyobb, mint az

A B C

háromszög köré írt

k

kör átmérője (13. ábra), hiszen nagyobb körben ugyanakkora kerületi szög ‐ ti. a

B A C = E A F

szög ‐ nagyobb húr felett nyugszik.
A

k

kör átmegy

P

-n is, és

A P

a kör egy átmérője, mert az

A B P C

négyszögben a

B

és

C

csúcsnál derékszög van. Elég tehát belátnunk, hogy

P

k'

kör belsejében van, hiszen ekkor

k'

-nek van

k

átmérőjénél nagyobb húrja, ezért

k'

átmérője nagyobb, mint

k

átmérője.

P

valóban

k

belsejében van, mert (8) alapján

\begin{matrix} E F P ∢ > B P C ∢ = 180^{\circ} - B A C ∢ = 180^{\circ} - E A F ∢, \end{matrix}

és az

E F

szakasz a

k'

kör (

A

-t nem tartalmazó)

E F

ívének pontjaiból látszik

180^{\circ} - E A F

szög alatt. Ennél nagyobb szög alatt az

E F

szakaszt csak a

k'

kör belső pontjaiból lehet látni. Ezt akartuk bizonyítani.

Scharnitzky Viktor, Lukács Ottó

¹Ugyanis az

F F_{1}

szakasz

P

-n átmenő felező merőlegesének ugyanazon oldalára esik

E

és

F_{1}