Cím:	Kombinatorika a geometriában, geometria a kombinatorikában, 2., befejező közlemény
Szerző(k):	Kárteszi Ferenc
Füzet:	1964/október, 49 - 53. oldal	PDF  |  MathML
Témakör(ök):	Szakmai cikkek

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.   (2., befejező közlemény)   6. Egyelőre tegyük félre eddigi témánkat ‐ később visszatérünk rá ‐ s fogjunk hozzá a következő, kombinatorikai kérdéskör tárgyalásához. Tekintsük az $N=n^2+n+1$ oldalú szabályos sokszög, $\Sigma$ csúcspontjainak a halmazát. Ennek elemei kettenként egyenes szakaszokat feszítenek ki; a szakaszok száma nyilvánvalóan $N\left(N-1\right)/2$. E szakaszok hosszúsága csak $\left(N-1\right)/2$-féle ‐ az egy csúcsból kiágazó ilyen szakaszok kettenként szimmetrikusan helyezkednek el, vagyis kettenként egyenlők; és minden egyes hosszúsághoz $N$ különböző szakasz tartozik ‐ a szakaszok bármelyikét a $K$ középpont körül, $\omega =2\pi /N$ szöggel egymás után $N$-szer elfordítjuk, ily módon az $N$ számú, egyenlő hosszú szakaszt mindegyik helyzetben megkapjuk. Ragadjunk ki a $\Sigma$ csúcsai közül $l$ számút, vagyis az $N$-elemű ponthalmaz egy $l$-elemű részhalmazát. Ez az $1$ pont kettesével $L=l\left(l-1\right)/2$ szakaszt feszít ki. Hogyha $l>n+1$, az $L$ számú szakasz közt előfordul két egyenlő hosszúságú, hiszen a $\Sigma$ által létesített szakaszok hosszúságai csak $\left(N-1\right)/2$-félék, és $l>n+1$ esetén $L>\left(N-1\right)/2$. Ha azonban $l=n+1$, akkor előfordulhat, hogy a szóban forgó, $l$-elemű részhalmaz kifeszítette $L$ számú húr mindegyike más‐más hosszúságú. 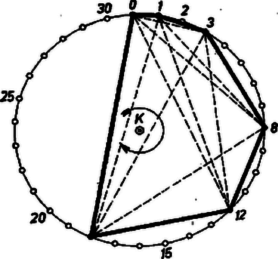    3. ábra   A 3. ábra példát mutat erre nézve, mégpedig az $5^2+5+1=31$ oldalú $\Sigma$ esetét. A kiválasztott $5+1=6$ elemű részhalmaz: a {0, 1, 3, 8, 12, 18} ponthalmaz. Elnevezhetnénk a $\Sigma$ ponthalmaz teljesen szabálytalan maximális részhalmazának. Egy ily módon definiált részhalmazt ‐ a rövidség kedvéért ‐ egy a $\Sigma$-hoz tartozó $\Pi$-halmaznak mondunk a következőkben. Az $n$ nem minden értéke esetében van a $\Sigma$ halmaznak $\Pi$‐részhalmaza. Ha pl. $n=6$, akkor bármiképpen választunk is ki a 43‐oldalú szabályos sokszög ‐ a $\Sigma$ sokszög ‐ csúcsai közül 7-et, e 7 pont kifeszítette szakaszok közt mindig van (legalább) két egyező hosszúságú, vagyis a kiválasztott részhalmaz a ,,teljesen szabálytalan'' követelménynek nem tesz eleget. (Erről az olvasó meggyőződhet, pl a 817. gyakorlat megoldásában alkalmazott módszerrel; az út hosszadalmas, kívánatos volna minél egyszerűbb megoldást keresni.) A $\Pi$ elemei által mint csúcsai által kifeszített $\left(n+1\right)$-oldalú konvex sokszöget a $\Sigma$ sokszög egy $\Pi$‐sokszögének mondjuk. A kutatások során igyekeztek megállapítani, hogy az $n$ mely értékei esetében van $\Sigma$-nak $\Pi$-részsokszöge, s mely értékek esetében nincs. Ez az általános kérdés azzal az elemi módszerrel, amellyel a mi feladat‐megoldóink az $n=3$ esetet tisztázták (817. gyakorlat), reménytelennek látszik. Valójában súlyos eszközöket használtak fel, mégsem oldották meg az egész problémát. Azt 1938-ban sikerült bebizonyítani, hogy minden $n=p^{\alpha }$ szám esetében (ahol $p$ prímszám és $\alpha =\mathrm{1,}\mathrm{2,}\mathrm{3,}\text{...})$ van a $\Sigma$-nak $\Pi$-részsokszöge. A következőkben a $\Sigma$‐halmaz bizonyos $\Pi$-részhalmazainak halmazával foglalkozunk.   7. Járjuk körül a szabályos $N$-szöget, a $\Sigma$-t, és mint az óraszámlapot, számozzuk meg a szögpontokat 0, 1, 2, $\text{...}$, $\left(N-1\right)$-gyel. Így kiragadva a $\begin{array}{c}{\displaystyle k_0<k_1<k_2<\text{...}<k_n}\end{array}$ számokat ‐ ahol is legyen $0\leqq k_0$ és $k_n\leqq N-1$ ‐, a $\Sigma$-nak egy részsokszögét, vagyis mint ponthalmaznak egy $\left\{k_0\mathrm{,}{k}_1\mathrm{,}\text{...}\mathrm{,}{k}_{n-1}\right\}$ részhalmazát jelöltük ki. Legyen ez most a $\Sigma$-nak egy $\Pi$-részhalmaza, mégpedig ama $\Pi$ sokszöggel megadva, melynek 0 és 1 szomszédos csúcsai és a $\overline{01}$ oldallal szomszédos két oldal közül a rövidebbik álljon a forgásirány felé. Ilyen a 3. ábra kiemelt hatszöge (ahol is $n=5$). Most forgassuk el a $K$ középpont körül a ${\Pi }_0$ sokszöget a kijelölt irányban rendre $\omega$, $2\omega$, $\text{...}$, $\left(N-1\right)\omega$ szöggel ‐ ahol $\omega =2\pi /N$ ‐, akkor a kezdő sokszöggel együtt a $\begin{array}{c}{\displaystyle {\Pi }_0\mathrm{,}{\Pi }_1\mathrm{,}{\Pi }_2\mathrm{,}\text{...}\mathrm{,}{\Pi }_{N-1}}\end{array}$ sokszögsorozatot kapjuk. Mondhatjuk, hogy ezek a sokszögek, mint elemek, egy újabb, $N$-elemű halmazt alkotnak; nevezzük ezt a halmazt $\Omega$-nak. A következőkben a $\Sigma$, $\Omega$ halmazok további kapcsolatait fogjuk kideríteni   I. TÉTEL: Az $\Omega$ halmaznak egy és csakis egy eleme tartalmazza a $\Sigma$ két adott elemét.   BIZONYÍTÁS. Legyen a $\Sigma$ két adott csúcsához írt szám a $k$ és $k+l$. E két pont $K$ pontból $l\omega$ szögben látszik. A ${\Pi }_0$ csúcsaiból alkotott pontpárok $K$ pontbeli látószögei közt az $\omega$, $2\omega$, $\text{...}$, $q\omega$ szögek $\left(q=\left(N-1\right)/2\right)$ mindegyike fellép, mégpedig mindegyik pontosan egyszer, ami a $\Pi$‐sokszög definiciójából következik. Tekintsük most ${\Pi }_0$-nak azt a csúcspontpárját, amelynek a látószöge éppen $l\omega$. Ezt a pontpárt az előírt irányú, $\begin{array}{c}{\displaystyle \mathrm{0,}\omega \mathrm{,}2\omega \mathrm{,}\text{...}\mathrm{,}\left(N-1\right)\omega }\end{array}$ szögű forgások közül egyik, de csak az egyik ‐ mondjuk a $j\omega$ szögű ‐ átviszi a $k$, $k+l$ kijelölt pontpárba. Ennélfogva az $\Omega$-nak egy és csak egy eleme, a ${\Pi }_j$ sokszög, tartalmazza mint csúcsokat a két adott pontot. Az így talált ${\Pi }_j$-t a $k$ és $k+l$ pontok összekötő sokszögének mondhatnánk.   II. TÉTEL: Az $\Omega$ bármely két elemének egy és csak egy közös csúcsa van, ami nyilvánvalóan a $\Sigma$-nak egy eleme.   BIZONYÍTÁS. Legyen a mondott két elem a ${\Pi }_k$ és ${\Pi }_{k+l}$ sokszög. A $K$ középpont körül a kijelölt irányba $l\omega$ szöggel elfordítva a ${\Pi }_k$-t, átmegy a ${\Pi }_{k+l}$-be. Minthogy ${\Pi }_k$-nak van egyetlenegy olyan csúcspontpárja, melynek $K$ pontbeli látószöge éppen $l\omega$, mondhatjuk, hogy ezt a párt a $q$ és $q+l$ pontok alkotják. Ámde az $l\omega$ szögű forgás $q$-t átviszi $\left(q+l\right)$-be, a ${\Pi }_{k+l}$ egy csúcsába. Eszerint a $q+l$ pont a ${\Pi }_k$ és ${\Pi }_{k+l}$ közös csúcsa. Több közös csúcs pedig az I. tétel szerint nem lehet. Az így talált, $q+l$ által megnevezett csúcsot a ${\Pi }_k$, ${\Pi }_{k+l}$ sokszögek metszés‐csúcsának mondhatjuk. Szembetűnő rokonság mutatkozik az I. és II. tétel közt a következő meggondolás során. Most ne törődjünk azzal, hogy a $\Sigma$ halmaz elemei pontok, az $\Omega$ halmaz elemei pedig $\Pi$‐sokszögek, hanem csak azt, hogy akár az egyik, akár a másik halmaz elemeinek a száma ugyanaz: $N=n^2+n+1$. Fogalmazzuk meg továbbá a két tételt a következőképpen:   I. A $\Sigma$ halmaz két eleme az $\omega$ halmaz egy és csak egy elemét ‐ összekötő sokszög ‐ határozza meg. II. Az $\Omega$ halmaz két eleme a $\Sigma$ halmaz egy és csak egy elemét ‐ metszés‐csúcs ‐ határozza meg. Ezt, a $\Sigma$ és $\Omega$ közt fennálló logikai szimmetriát dualitásnak nevezzük. III. TÉTEL. Kiválasztható a $\Sigma$ elemei közül négy olymódon, hogy azok kettenként hat összekötő $\Pi$-sokszöget határoznak meg.   BÍZONYÍTÁS. Tekintsük a ${\Pi }_0$ és ${\Pi }_1$ sokszöget. E két sokszög közös csúcsa az 1. Legyen ${\Pi }_0$-nak az 1-től különböző két csúcsa $j$ és $h$; az ${\Pi }_1$-nek az 1-től különböző két csúcsa pedig $k$ és $l$. A $j$, $h$, $k$, $l$ pontok kettenkénti összekötő $\Pi$‐sokszögei közül már kettő megvan: a ${\Pi }_0$ és ${\Pi }_1$. Ezek egyike sem lehet a $j$, $k$ párt összekötő $\Pi$-vel azonos, mert különben a másikkal is volna az 1-en kívül még egy közös csúcsa, ámde akkor az I. tétel szerint ezzel a másikkal is azonos volna, ami nem igaz, mert ${\Pi }_0$ nem azonos a ${\Pi }_1$-gyel. Hasonló eredmény adódik a $j\mathrm{,}l$; $h\mathrm{,}k$; $h\mathrm{,}l$ párokra nézve is. Még a $j\mathrm{,}k$; $j\mathrm{,}l$; $h\mathrm{,}k$; $h\mathrm{,}l$ párok meghatározta $\Pi$‐sokszögeket kell egymással egybevetni. Hogyha pl. a $j$, $k$ meghatározta $\Pi$‐sokszög a $j$, $l$ meghatározta $\Pi$-vel volna azonos, akkor ez a $\Pi$ a $j$, $k$, $l$ szögpontokat mind összekötné, amiből újra az adódik, hogy ${\Pi }_0$ a ${\Pi }_1$-gyel azonos, és ez nem igaz. Ugyanígy adódik a többi esetben is, hogy a párok meghatározta $\Pi$‐sokszögek páronként különbözők.   8. Ezek után a sík és a síkgeometria, pontosabban a projektív sík és projektív síkgeometria legkorszerűbb felfogását is ismertetni tudjuk. Hogyha ,,egy sík összes pontjain'' valamely $\Sigma$-nak az összes csúcsait, valamint ,,a sík összes egyenesein'' a $\Sigma$-hoz tartozó $\Omega$ összes elemeit ‐ a ${\Pi }_0$, ${\Pi }_1$, $\text{...}$, ${\Pi }_{N-1}$ sokszögeket ‐, továbbá ,,egy egyenes pontjain'' egy $\Pi$‐sokszög csúcsait akarjuk érteni, akkor ez a mesterkélt fogalomalkotás nem vezet az I axiómarendszerrel szembeni ellentmondásra. (Így csak az derül ki, hogy az axiómarendszer ‐ noha a közönséges sík ideális elemekkel való bővítésével származtatott projektív sík jellemzésére készült ‐ másféle elemrendszereket is jellemez.) Ebben az értelemben ugyanis az ${\text{<span style="font-weight: bold;">I</span>}}_1$, ${\text{<span style="font-weight: bold;">I</span>}}_2$, ${\text{<span style="font-weight: bold;">I</span>}}_3$ axiómák rendre ugyanazt mondják, amit az I., II., III. tételek. Ilyen mesterkélt sík végtelenül sokféle van, mert ahogyan a 6. szakaszban említettük, minden törzsszám‐hatványhoz tartozik $\Pi$‐részsokszöggel rendelkező $\Sigma$ sokszög. Az így definiált síkot $n=p^2$‐adrendű GALOIS síknak nevezik. Bármiféle elemek halmazát tekintjük is, ha abban az ${\text{<span style="font-weight: bold;">I</span>}}_1$, ${\text{<span style="font-weight: bold;">I</span>}}_2$, ${\text{<span style="font-weight: bold;">I</span>}}_3$ axiómákban szereplő fogalmak értelmezhetők, és az adott értelmezések szerint igazak is az axiómák állításai, akkor a halmazt projektív síknak nevezik. Az axiómarendszernek megfelelő különféle síkokra azt is szokták mondani, hogy az axiómarendszer által definiált modellek. Eddig tehát az I által definiált modellekkel ismerkedtünk, de nem minden modellel, hanem csak a közönséges síkból bővítéssel származtatott végtelen modellel és a véges modellek közül a GALOIS‐félékkel. A ,,végtelen'' és ,,véges'' arra utal, hogy a sík pontjainak száma végtelen vagy véges. Az I-ből tehát ‐ további tulajdonságok ismerete nélkül ‐ nem lehet levezetni még azt sem, hogy az egyenesnek végtelen sok pontja van, hiszen amint láttuk, az olyan modellre nézve is igazak az I axiómái, amelynek minden egyenese $n+1=p^{\alpha }+1$ pontból áll. Az axiómarendszer éppen azt mondja ki, ami az általa definiált modellek közös tulajdonsága; és minden pusztán az axiómákból levezethető tétel a modellek mindegyikére nézve, vagyis közösen igaz. Talán első hallásra meglepő az az állitás, hogy a FANO‐tétel az I-ből nem vezethető le. Hiszen láttuk, hogy a közönséges sík bővítésével származtatott projektív síkon ‐ klasszikus projektív síknak is nevezik ‐ az F-tétel igaz. A 3-adrendű GALOIS sík tanulmányozása során kiderülne, hogy az F‐tétel azon is igaz. Most megmutatjuk, hogy például a 2‐odrendű GALOIS síkon az F‐tétel nem igaz. 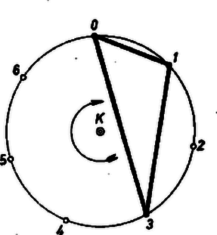    4. ábra   A másodrendű GALOIS sík (4. ábra) a közönséges sík szabályos hétszögével azonos, egyeneseit a ${\displaystyle \begin{array}{cc}\hfill {\displaystyle 0^{*}}& {\displaystyle =\left\{\mathrm{0,}\mathrm{1,}3\right\}\mathrm{,}{1}^{*}=\left\{\mathrm{1,}\mathrm{2,}4\right\}\mathrm{,}{2}^{*}=\left\{\mathrm{2,}\mathrm{3,}5\right)\mathrm{,}}\hfill \\ \hfill {\displaystyle 3^{*}}& {\displaystyle =\left\{\mathrm{3,}\mathrm{4,}6\right\}\mathrm{,}{4}^{*}=\left\{\mathrm{4,}\mathrm{5,}0\right\}\mathrm{,}{5}^{*}=\left\{\mathrm{5,}\mathrm{6,}1\right\}\mathrm{,}{6}^{*}=\left\{\mathrm{6,}\mathrm{0,}2\right\}}\hfill \end{array}}$ háromszögek jelentik. Tekintsük most ‐ például a 0, 2, 3, 4 pontnégyest. A pontnégyes elemei kettenként a ${\displaystyle \begin{array}{c}\hfill {\displaystyle }\end{array}}$ [0,2]={6,0,2}=6*,[3,4]={3,4,6}=3*; [0,3]={0,1,3}=0*,[2,4]={1,2,4}=1*; [0,4]={4,5,0}=4*,[2,3]={23,5}=2* összekötő egyeneseket feszítik ki. Ezeket már úgy osztottuk párokba, soronként írva a párokat, hogy az egyenespár egyik egyenese a pontnégyes valamelyik pontpárját, másik egyenese a pontnégyes hátra levő két pontját köti össze. Vagyis a $\begin{array}{c}{\displaystyle 6^{*}\mathrm{,}{3}^{*};0^{*}\mathrm{,}{1}^{*};4^{*}\mathrm{,}{2}^{*}}\end{array}$ párok metszéspontjai az átlóspontokat jelentik. Lássuk csak e ponthármaspárok közös elemét! A részletes kiírásukból közvetlenül kitűnik, hogy rendre a $\begin{array}{c}{\displaystyle \mathrm{6,}\mathrm{1,}5}\end{array}$ pontokról van szó. Lám! ez a három átlóspont most nem háromszöget, hanem egyenest feszít ki: az $5^{*}=\left\{\mathrm{5,}\mathrm{6,}1\right\}$ egyenesről van szó.   9. Befejezésként azt emeljük ki, hogy az I-ből pusztán következtetéssel adódó tétel az I-nek megfelelő bármely modellre nézve érvényes, hiszen az összes lehetséges modellek közös tulajdonságából, az I-ből indul ki az ilyen levezetés. Példaképpen lássunk egy ilyen ,,sok legyet egy csapással'' jellegű levezetést.   Legyen $a$ és $b$ két egyenes, $P$ pont pedig egyikhez se illeszkedjék. Tétel: $P$-ből $a$ pontjait $b$-re vetítve az utóbbinak minden pontját megkapjuk és mindegyiket csak egyszer. Bizonyítás: legyen $X$ az $a$-nak egyik tetszőleges pontja. Az ${\text{<span style="font-weight: bold;">I</span>}}_1$ szerint egy $PX$ egyenes, röviden $x$ egyenes van. Ez az $x$ sem $a$-val, sem $b$-vel nem azonos, mert az utóbbiaknak $P$ nem eleme, viszont $x$-nek eleme. No de akkor az $x$ és $b$ egyenespárnak ${\text{<span style="font-weight: bold;">I</span>}}_2$ szerint van egy közös $Y$ pontja, sőt ${\text{<span style="font-weight: bold;">I</span>}}_1$ szerint csak egy ilyen van. Az $Y$ a $P$-től különbözik, mert $Y$ a $b$ egyenesnek eleme, viszont a $P$ nem. Az $a$ egyenes két pontjának, $X_1$ és $X_2$-nek nem lehet ugyanaz az $Y$ pont a $b$-re eső vetülete. Az $x_1$ és $x_2$ ugyanis nem lehet azonos, mert az $X_1$ et és $X_2$-t egyaránt tartalmazó egyenes, az $a$, nem tartalmazza $P$-t. Másrészt az egymástól különböző $x_1$, $x_2$ egyeneseknek $P$ is és $Y$ is közös pontja volna, ami ${\text{I}}_2$ szerint lehetetlen. Ezek szerint az $a$ pontjait vetítve a $b$ egyenes más‐más pontjait kaptuk. Azt kell mqg belátnunk, hogy így a $b$-nek minden pontja előáll. Vegyük evégből $b$ egy tetszőleges $V$ pontját. A $PV$ összekötő egyenes, röviden $u$, egy $U$ pontban metszi $a$-t. Ennek az $U$-nak a $P$-ből való vetülete a $V$. Bizony kínosan nehézkesnek látszik ez a csupán I-re támaszkodó okoskodás. Ámde megéri a fáradozást, mert a tétel végtelen sok modell bármelyikére igaz dolgot állít. Érdemes legalább egy modellen megnézni, hogy mit mond e tétel. Vegyük evégből és gyakorlásképpen a harmadrendű GALOIS síkot, vagyis a szabályos 13-szöget, melyben a $\Pi$‐sokszögek négyszögek. (Most már az ábrakészítést és annak alapján az egyeneseket jelentő számnégyesek összeállítását, ami a 8. szakaszban tárgyaltak mintájára megy, az olvasóra bízzuk.) Az egyenesek: ${\displaystyle \begin{array}{c}\hfill {\displaystyle 0^{*}=\left\{\mathrm{0,}\mathrm{1,}\mathrm{3,}9\right\}\mathrm{,}{1}^{*}=\left\{\mathrm{1,}\mathrm{2,}\mathrm{4,}10\right)\mathrm{,}{2}^{*}=\left\{\mathrm{2,}\mathrm{3,}\mathrm{5,}11\right\}\mathrm{,}\text{...}\mathrm{,}}\hfill \\ \hfill {\displaystyle {12}^{*}=\left\{\mathrm{12,}\mathrm{0,}\mathrm{3,}8\right\};}\hfill \end{array}}$ ahol is $k^{*}$ a ${\Pi }_k$ sokszög csúcspontjainak halmaza. Legyen most a $P$ vetítési középpont szerepét betöltő elem az 5. Továbbá az $a$, $b$ szerepét vegye át a $0^{*}$, $1^{*}$. Két sorban felírjuk a $0^{*}$ és $1^{*}$ pontjait, mégpedig az első sor elemei alá rendre a vetületeket írva: $\begin{array}{c}{\displaystyle \left({\displaystyle \begin{array}{cccc}\hfill {\displaystyle 0}\hfill & \hfill {\displaystyle 1}\hfill & \hfill {\displaystyle 3}\hfill & \hfill {\displaystyle 9}\\ \hfill {\displaystyle 4}\hfill & \hfill {\displaystyle 1}\hfill & \hfill {\displaystyle 2}\hfill & \hfill {\displaystyle 10}\end{array}}\right)}\end{array}$ A vetítő egyenesek sugársorát rendre a $4^{*}$, $5^{*}$, $2^{*}$, $9^{*}$ egyenesek alkotják.   10. A GALOIS geometriáról szóló első nagyszabású, úttörő jellegű mű, mely erre a kutatási területre a matematikusok fokozott érdeklődését ráirányította, 1959-ben jelent meg. Szerzője B. SEGRE professzor, a nagyhírű római ,,Seminario di Algebra Geometria e Topologia'' igazgatója. Ma már az ő tanítványai művelik ezt az új tudományágat, s rövid néhány esztendő alatt számos szép eredményt értek el. B. SEGRE professzor 1963-ban töltötte be hatvanadik életévét, jelen közleményemet az ő tiszteletére írtam.    Kárteszi Ferenc