Cím: Kombinatorika a geometriában, geometria a kombinatorikában, 1. közlemény
Szerző(k):  Kárteszi Ferenc 
Füzet: 1964/szeptember, 7 - 11. oldal  PDF  |  MathML 
Témakör(ök): Szakmai cikkek

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

1. A matematika története tanusítja, hogy egyes problémakörök iránt koronként kialszik az érdeklődés, majd megújulva ismét fellángol. Előfordul, hogy a kutatások során olyan, az eredeti problémakörből kiágazó izgalmas kérdések merülnek fel, amelyek elvonják az érdeklődést, s más irányba terelik a kutatókat. Lehet az is, hogy a matematikának és alkalmazásainak bizonyos fejlődési stádiumában valamely problémakör annyira kiaknázottnak látszik, hogy semmi újat nem ígér. Az ilyen ,,kimerült bányától'' a kutató szellem elfordul és újat, feltárásra érdemest keres. Az elhanyagolt vagy elhagyott kutatási területekre való visszatérésnek különféle indítékai lehetnek. Előfordul, hogy valamely problémakör a fejlődés során érintkezésbe jut egy régi, azelőtt tőle távolinak látszó problémakörrel. Ilyenkor az egyiknek a módszerei és szempontjai behatolnak a másiknak a területére, sőt esetleg kölcsönösen megtermékenyítik egymást. Megújhódik a régi, a lezárt kérdések új fényt kapnak és új problémákat vetnek fel. Gyakran előfordul, hogy valamely régi módszer vagy lezárt ismeretkör hasznos alkalmazásra talál, és ilymódon ismét az érdeklődés előterébe lép. Ilyenkor esetleg éppen az alkalmazók veszik észre, hogy a régen kidolgozottnak és lezártnak vélt terület koránt sincs kidolgozva és lezárva, újjá kell építeni vagy át kell alakítani és tovább kell fejleszteni.
Ebben a közleményben a matematika egy olyan legújabb kutatási területére vezetjük el az olvasót, amely két régi ismeretágnak, a projektív geometriának és a kombinatorikának a találkozásából született, s ma már alkalmazásra is talált a fizikában és a matematikai statisztikában.
Igyekszünk úgy tálalni mondanivalóinkat, hogy az iskolai tananyagon túli előismeretek nélkül is érthető legyen. E folyóirat múlt tanévi füzeteiben néhány feladat a jelen közlemény előkészítésére szolgált: 817. gyakorlat, 1224. és 1284. feladat.1 Hogyha a kombinatorika elnevezéssel itt találkozott először az olvasó, egyelőre elég, ha csak annyit tud róla, hogy az idézett feladatok geometriai tárgyú és kombinatorikai jellegű okoskodással megoldott feladatok. (A kezdő számára nem sokat jelentene, ha azt mondanánk: a kombinatorika nem más, mint a véges halmazok elmélete.) Azt pedig, hogy mivel foglalkozik a projektív geometria, kissé részletesebben, de csak a legszükségesebb tudnivalókat érintve, megvilágítjuk. Csakis a síkgeometriáról beszélünk, ezért ha nem is mondjuk ki, mindig úgy értendő, hogy a szóban forgó pontok és alakzatok egy síkhoz tartoznak.

 

2. Olyan alakzatokkal és ezeknek olyan tulajdonságaival foglalkozunk, amelyek a pont, egyenes és illeszkedés fogalmával teljesen leírhatók. ‐ Illeszkedés a pont és egyenes ama kölcsönös viszonyát jelenti, amit más szóval így szoktunk kifejezni: ,,a pont rajta van az egyenesen'', avagy ugyanazt jelenti: ,,az egyenes átmegy a ponton''. Bármely pont‐egyenes pár esetében tudjuk azt, hogy vagy az illeszkedés, vagy a nem‐illeszkedés viszonya áll fenn köztük. ‐ Az összekötő egyenes és a metszéspont a mondott három fogalom segítségével definiálható. Az az egyenes, mely két ponthoz egyaránt illeszkedik, a két pont összekötő egyenese. Az a pont, mely két egyeneshez egyaránt illeszkedik, a két egyenes metszéspontja.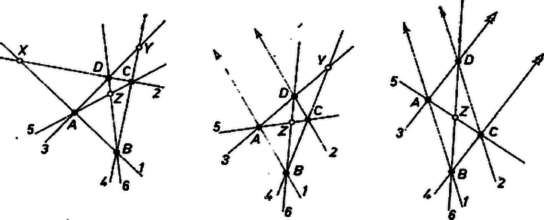
 
 
1. ábra a, b, c,
 

Általános pontnégyes az olyan négyelemű ponthalmaz, mely (kettesével) hat összekötő egyenest határoz meg, vagyis nem létezik egyenes, melyhez a négy pont közül kettőnél több is illeszkedik.
Az általános pontnégyes kifeszítette hat egyenes alakzatát tekintve, három esetet kell megkülönböztetnünk, amint az 1. ábra a), b), c) részei mutatják. Az ABCD pontnégyes kifeszítette 1, 2, ..., 6 egyeneseket ugyanis párokra bontjuk, a következő rendezési elv szerint. Az egyenesek bármelyike a pontnégyes két elemét köti össze, a másik két pontot összekötő egyenes legyen az előbbinek a párja. Az így definiált 1, 2, 3, 4, 5, 6 egyenespárok elemei ‐ az a) esetben ‐ az X, Y, Z metszéspontokat, az eredeti pontnégyes átlóspontjait szolgáltatják. A b) esetben csak két átlóspont (Y és Z), a c) esetben csak egy átlóspont (Z) lép fel, mert az 1 és 2; illetve az 1 és 2, valamint a 3 és 4 egymást nem metsző egyenesek.
 
Az eseteknek megfelelően könnyű bebizonyítani a következő tételeket:
α: Az X, Y, Z pontok (kettenként) három összekötő egyenest határoznak meg.
β: Az YZ összekötő egyenes mind az 1, mind a 2 egyenest metszi (vagyis nem párhuzamos velük).
γ: A Z ponton átmenő, az 1, 2 egyenespárt nem metsző (vagyis a pár elemeivel párhuzamos) egyenes különbözik a Z ponton átmenő és a 3, 4 egyenespárt nem metsző egyenestől.
E tételek bizonyítását az olvasóra bízzuk.
 

A szóban forgó háromféleséget az a kétféleség okozza, hogy két egyenesnek vagy van egy közös pontja vagy nincs (vagyis párhuzamosak).
J. KEPLER (1571‐1630), a nagy csillagász észrevette, hogy ha a sík pontjai alkotta ponthalmazt új elemek bevezetésével kibővítjük, akkor az ilyen fajta többféleségek megszüntethetők. (Elgondolása arra a fogalomalkotó eljárásra emlékeztet, mely a természetes számok alkotta halmaz első bővítésekor szerepel, midőn bevezetjük az új elemet, a zérust.) A sík fogalmának e KEPLER‐féle megváltoztatását most a szükséges mértékben ismertetjük.
 
3. A sík eddigi értelemben vett pontjait és egyeneseit egyelőre közönséges pontoknak és közönséges egyeneseknek mondjuk. A közönséges egyenes pontjainak a halmazát egy új elemmel, az egyenes ideális pontjával bővítjük; két egyenes pontjainak a halmazát akkor és csak akkor bővítjük ugyanazzal az ideális ponttal, hogyha a két egyenes párhuzamos. Az ideális pont értelmét éppen az a kijelentés fejezi ki, hogy a párhuzamos egyeneseknek egy közös ideális pontjuk van, ez a pont illeszkedik a mondott egyenesekhez, de nem illeszkedik a mondott egyenesekkel nem párhuzamos egyenesek egyikéhez sem.
Az ideális pontok bevezetése után elmondhatjuk, hogy két egyenes mindig metszi egymást egy pontban, tudniillik vagy közönséges pontban, vagy ideális pontban.
Mi lesz most azzal az alaptétellel az így bővített síkon, hogy két ponthoz egy és csak egy egyenes illeszkedik (az összekötő egyenes)?
Evégből azokat az eseteket kell, mint új lehetőségeket, tekintetbe vennünk, midőn nem mindkettő közönséges pont. Először is legyen adva egy közönséges pont, P és egy ideális pont, jelölje ezt Q∞. Mit jelent az, hogy adva van a Q∞? Azt, hogy adva van egy l egyenes, ennek egy ideális pontja van, és az legyen a Q∞. A Q∞-hez illeszkedő egyenesek az l-lel párhuzamos egyeneseket jelentik. Ezek közül az egyenesek közül ‐ tudjuk ‐ egy és csak egy megy át a P ponton. Ez az egyenes most a P és Q∞ összekötő egyenese. Tehát az alaptétel ebben az esetben is igaz. Hogyha két ideális pont van adva, ez úgy értelmezhető, hogy adva van két, egymást közönséges pontban metsző egyenes, k és l. Az előbbinek az ideális pontját jelölje P∞, az utóbbiét Q∞. Most a P∞ Q∞ összekötő egyenes értelmét veszti, mert egy egyenesnek csak egyetlenegy ideális pontja van. Ezt a kivételt is megszüntetjük azáltal, hogy a sík egyeneseinek a halmazát egyetlenegy új elemmel, a sík ideális egyenesével bővítjük. Az ideális egyenesnek csak ideális pontjai vannak, az összes ideális pontok ehhez az egyeneshez tartoznak (illeszkednek). Így tehát a P∞Q∞ összekötő egyenes nem más, mint a sík ideális egyenese.
A sík ideális egyenesének bevezetése után, nem téve különbséget a közönséges és az ideális pont között, kimondhatjuk az alaptételt: két ponthoz egy és csak egy egyenes illeszkedik, ez a két pont összekötő egyenese. Vagyis az ideális pontokkal és az ideális egyenessel bővített sík, az ún. projektiv sík olyan, hogy azon igaz marad ez a régi alaptétel. Viszont az a kétféleség, hogy ,,két egyenes vagy metszi egymást vagy nem'', megszűnt. Két egyenesnek abban az esetben is van közös pontja (metszéspontja), midőn az egyik a sík ideális, a másik pedig egy közönséges egyenese. Ez a pont nem más, mint a mondott közönséges egyenes ideális pontja. A projektív síkon tehát ‐ nem téve különbséget az ideális és közönséges pontok között, valamint ideális és közönséges egyenesek közt ‐ egy új alaptétel igaz: bármely két egyenesnek van egyetlenegy közös pontja, ez a két egyenes metszéspontja.
 

4. Visszatérünk az 1. ábrához, s az ideális elemek fogalmát felhasználva, egybevetjük az a), b), c) alakzatokat. ‐ Rövidség kedvéért az elem ideális voltára a ,,∞'' jel index gyanánt való kiírásával utalunk. ‐ A b) alakzat 1, 2 egyenesei X∞ ideális átlóspontot szolgáltatják és a β) most úgy mondható, hogy az X∞, Y, Z pontok nem köthetők össze egyetlenegy egyenessel. A c) alakzatnak pedig két ideális átlóspontja van, X∞ és Y∞. Most az X∞Y∞ összekötő egyenes az ideális egyenes, tehát a közönséges Z pont nincs rajta, vagyis X∞, Y∞, Z pontok most sem köthetők össze egyetlenegy egyenessel.
Kiemelve a három eset közös tartalmát, mondhatjuk: a közönséges pontokból álló ABCD pontnégyes átlóspontjai egy háromszöget alkotnak (melynek legalább egy közönséges csúcspontja van).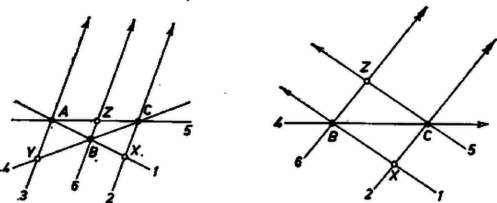
 
 
2. ábra d, e
 

Ezen az úton haladva új kérdés merül fel. Az a kikötés ugyanis, hogy az A, B, C, D pontok közül kettőnél több ne essék egy egyenesbe, vagyis kettenként hat egyenest határozzanak meg, úgy is teljesülhet, hogy a négy pont közül vagy egy, vagy kettő legyen ideális pont. Mit veszünk észre ezekben az esetekben? A 2. ábra d) alakzata az A, B, C, D∞ és e) az A∞, B, C, D∞ esetet tünteti fel. A második esetben az egyik átlóspont és az egyik összekötő egyenes is ideális elem: Y∞ és 3∞. Az eseteknek megfelelően igaz a következő tétel:
δ) Az X, Y, Z átlóspontok (kettenként) három összekötő egyenest határoznak meg.
ε) Az XZ egyenes közönséges pontban metszi az Y ponton átmenő 4 egyenest.
E tételek bizonyítását az olvasóra hagyjuk.
 

Most pedig megmondjuk, hogy a sík fogalmának KEPLER‐féle módosítása miként teszi lehetővé az ötféle tétel ‐ α), β), γ), δ), ε) ‐ megegyező lényegének megragadását, egyetlen tételként való megfogalmazását. Evégből megszüntetjük a közönséges és ideális pont megkülönböztetést, vagyis a projektív sík értelmében fogalmazunk.
 

Hogyha egy pontnégyes elemei hat összekötő egyenest határoznak meg, akkor az általa meghatározott három átlóspont három összekötő egyenest határoz meg.
Ez az ún. FANO‐féle tétel (röviden F‐tétel).
 

5. A projektív sík fogalma és az ún. projektív geometria a matematikusok körében eleinte alig váltott ki érdeklődést. A projektív geometria első fejlődési periódusa J. V. PONCELET (1788‐1867) francia matematikus 1822-ben megjelent híres művével kezdődött: ,,Trailé des propriétés projectives des figures.''1 Ettől fogva rohamos fejlődésnek indult, a matematikusok érdeklődésének egyik középponti témája lett. Fejlődése több ízben kihatott az algebrára is, termékeny szempontokkal és problémákkal gazdagította. Egy évszázadot átívelő fejlődése után úgy látszott, hogy a ,,kimerült bánya'' sorsára jut. Azonban 1943-ban ismét megújhodva ‐ újfajta problémákkal ‐ magára vonta a figyelmet. A jelen közlemény következő részében a projektív geometria e legújabb kérdésköreiből adunk ízelítőt.
Egy évszázados fejlődés során számos olyan művet publikáltak, melynek az volt a célja, hogy néhány egyszerű alapfogalomból, s lehetőleg kisszámú alaptételből (axiómából) kiindulva vezessék le a projektív geometria egészét. Ebben a kutató munkában éppen az alapul szolgáló legalkalmasabb fogalmak és tételek kiválogatása, összeállítása volt a nehéz. Harmadik évtizede ‐ de különösképpen nyolc esztendő óta ‐ egy itt ismertetésre kerülő axiómarendszer, röviden I, valamint az I-re támaszkodó okoskodások útján adódó tételek tanulmányozása több neves matematikust foglalkoztat.
A szóban forgó axiómák a projektív sík jellemzésére szolgálnak, és a sík alapeleméül a pontot választva, a síkot mint ponthalmazt tekintjük. Az egyenes mint e halmaz bizonyos részhalmaza értelmezhető. Az I rendszer három axiómája éppen azt mondja meg, hogy melyek azok a tulajdonságok, amelyek az egyenesnek nevezett részhalmazt, és csakis azt jellemzik.
I1 axióma: Két pont egy és csak egy egyenesnek két pontja.
I2 axióma: Két egyenesnek van közös pontja.
I3 axióma: Létezik olyan négy pont, amely (az I1 értelmében) hat egyenest határoz meg.
Az I1-ből és I2-ből következik, hogy két egyenesnek csak egy közös pontja van. Ezeket az axiómákat az összekötés, a metszés és a négyszög alaptételének is szokás mondani.
Az I1, I2 és I3 axiómákra, röviden az I-re támaszkodva, a következő tételt már könnyű levezetni:
Létezik olyan négy egyenes, amely az I2 értelmében hat pontot határoz meg.
 
Kárteszi Ferenc
1K. M. L. 27 (1963/12) 213. és 202 o. (megoldással), ill. 221. o. (kitűzés).

1Magyarul: Alakzatok projektív tulajdonságairól.