Cím: 1963. évi Kürschák József matematikai tanulóverseny feladatainak megoldása
Szerző(k):  Hajós György 
Füzet: 1964/április, 146 - 153. oldal  PDF  |  MathML 
Témakör(ök): Kürschák József (korábban Eötvös Loránd)

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Első feladat. Egy teremben p sorban és q oszlopban pq szék van (p>1,q>1). Minden széken egy-egy tanuló ül, mind különböző magasságú. A tanár minden sorból kiszemeli a legkisebbet, ezek legnagyobbikának magassága a. Azután minden oszlopból kiszemeli a legnagyobbat, ezek legkisebbikének magassága b. Eldöntendő, hogy az a<b, a=b, a>b esetek közül melyek lehetségesek, s hogy minden lehetséges eset bekövetkezése biztosítható-e az ülésrend megváltoztatásával.

 

Megoldás. Nevezzük egyszerűség kedvéért az a magasságú tanulót a-nak, a b magasságút b-nek, stb. Tekintsük a sorát és b oszlopát. E sor és oszlop kereszteződésében elhelyezkedő széken is ül egy tanuló. Ennek magasságát c-vel jelöljük.
Számolunk azzal a lehetőséggel, hogy a, b, c nem mind különbözők. Ha ugyanis a és b egy sorban ül, akkor c azonos b-vel. Ha a és b egy oszlopban ül, akkor c és a azonos. Ha pedig a azonos b-vel, akkor c is azonos velük.
Minthogy a és c egy sorban ül, és a a sorában a legkisebb, c-nél sem lehet nagyobb, azaz a≤c. Ugyanígy adódik, hogy c≤b, hiszen c és b egy oszlopban ül, és b az oszlopában a legnagyobb. Ezek szerint a≤c≤b, tehát a≤b, vagyis: az a>b eset nem következhetik be.
Az a=b eset bekövetkezik, ha pl. az utolsó sorba a legnagyobb tanulókat ültetjük. Ekkor az utolsó sorban ülők legkisebbike egyaránt betölti a és b szerepét, mert egyrészt a sorában nincs nála kisebb, de minden más sorban van, másrészt az oszlopában nincs nála nagyobb, de minden más oszlopban van.
Az a<b eset bekövetkezik, ha pl. az előző elrendezésből indulunk ki, de az utolsó sor legkisebb tanulója helyet cserél az oszlopában ülő valamelyik másik tanulóval. Az előreültetett tanuló a helycsere után is változatlanul betölti b szerepét, hiszen oszlopában nincs nála nagyobb, de minden más oszlopban van. Minthogy azonban az előreültetett tanuló új sorának minden más tanulója nála kisebb, a keresésekor ő még az egyes sorokból kiszemelt legkisebbek között sem szerepel, s így a szerepét nem ő tölti be.
 

Megjegyzés. 1. A feladat p>1, q>1 megszorítását kihasználtuk akkor, amikor ugyanabban az oszlopban ülő másik tanulóról, s amikor ugyanabban a sorban ülő minden más tanulóról szóltunk. A megszorításra szükség van, mert ha a székek egyetlen sorban vagy egyetlen oszlopban helyezkednek el, akkor nyilván a legkisebb, illetőleg a legnagyobb tölti be egyszerre a és b szerepét. Ilyenkor tehát csak az a=b eset valósulhat meg.
 

2. Felvetjük a kérdést, hogy minden tanuló számolhat-e azzal a lehetőséggel, hogy a szerepét majd ő tölti be. Ugyanezt kérdezzük a b szerepet illetően is. Azt állítjuk, hogy a legkisebb p-1 tanuló és a legnagyobb q-1 tanuló egyik szerep betöltésekor sem jöhet szóba.
a esetében ez abból következik, hogy a a saját sorának legkisebbike, tehát a sorában van q-1 nála nagyobb tanuló, viszont minden más sorban van a-nál kisebb, azaz van legalább p-1 nála kisebb tanuló. Hasonlóan okoskodhatunk b esetében is, mert a saját oszlopában p-1 nála kisebb tanuló ül, és minden más oszlopban van nála nagyobb, azaz legalább q-1 nála nagyobb tanuló van.
Ha tehát a tanulókat a legkisebbtől kezdve megszámozzuk, akkor csak a
p,p+1,p+2,...,pq-q+1
sorszámú tanulók tölthetik be az a, b szerepeket.
 

3. Eddigi megállapításaink bizonyos korlátozásokat tartalmaztak. Azt kérdezzük most, hogy ezeket a korlátozásokat figyelembe véve minden eset megvalósulhat-e. Pontosabban szólva a következő kérdést vetjük fel: A tanár a teremben elhelyezkedő székek egyikére a jelet, egy másikra vagy esetleg ugyanarra b jelet tesz; ezután a folyosón gyülekező tanulókat nagyság szerint sorba állítja, és a p, p+1, ..., pq-q+1 sorszámu tanulók közül kijelöl egyet vagy kettőt aszerint, hogy a teremben ugyanarra a székre tette-e az a és a b jelet, vagy sem, mégpedig abban az esetben, amikor a megjelölt székek nincsenek sem egy sorban, sem egy oszlopban, akkor két olyan tanulót jelöl ki, akik a nagyság szerinti sorban nem állnak egymás mellett; kérdés, hogy elhelyezhetők-e a tanulók a teremben úgy, hogy a megjelölt székekre a kijelölt tanulók üljenek, mégpedig, ha ketten vannak, akkor a kisebbikük üljön az a jelű székre, s hogy a és b szerepét éppen az a és b jelű széken ülő tanuló töltse be.
Azt állítjuk, hogy ez mindig lehetséges. Meg kell említenünk, hogyha a megjelölt székek nincsenek sem egy sorban, sem egy oszlopban, akkor megoldásunk értelmében szerepelnie kell egy a-nál nagyobb és b-nél kisebb c tanulónak, s ezért a és b a nagyság szerinti sorban nem állhattak egymás mellett. Ez az eset természetesen csak akkor valósítható meg, ha a p, p+1, ..., pq-q+1 sorszámú tanulók száma 2-nél nagyobb, azaz
pq-p-q+2>2,(p-1)(q-1)>1,


vagyis ilyenkor a p, q értékek között kell 2-nél nagyobbnak lennie. Eszerint bizonyos kivételt jelent a p=q=2 eset, mert ekkor a 4 szék közül nem szabad két átlósan elhelyezkedőt megjelölni. Ha ugyanis a tanár így járna el, akkor nem tudna a folyosón az előírást betartva kijelölni két tanulót.
Állításunk bizonyítása érdekében először is azt említjük meg, hogy a teremben a sorokat is és az oszlopokat is szabadon felcserélhetjük a rajtuk ülőkkel együtt; ez nem változtat azon, hogy ki tölti be az a, b szerepeket. Ezért nem jelent megszorítást, ha csak azokkal az esetekkel foglalkozunk, amikor az a jelű szék az utolsó sor bal szélén áll, a b jelű szék pedig az első vagy az utolsó sor valamelyik szélső széke. Nevezzük a p-1 legkisebb tanulót ,,kicsinek'', a q-1 legnagyobb tanulót pedig ,,nagynak''.
Ha a b jel is az utolsó sor bal szélső székére került, akkor a kijelölt egyetlen tanulót erre a székre ültetjük, az utolsó sor többi székére a nagyokat, a bal szélső oszlop többi székére a kicsiket, a még el nem foglalt székekre pedig a többi tanulót ültetjük. Ilyenkor valóban az egyetlen kijelölt tanuló jut az a, b szerepek mindegyikéhez.
 
 
1. ábra
 

A többi esetben ábrán mutatunk be a követelményt kielégítő elrendezést (1. ábra). Az ábra a p=4, q=5 esetre készült, de módszere minden p>1, q>1 esetben alkalmazható. A kicsik helyét pont, a nagyok helyét kör jelöli. Az ábrán meg nem jelölt helyeken a többi tanuló tetszés szerint helyezkedhetik el. Ha a és b átellenes sarkokban van, akkor c olyan tanulót jelöl, akit a nagyság szerinti sorban a és b közrefog. Erre az esetre ábránk két elrendezést mutat be. Az első akkor alkalmazható, ha q>2, a második pedig akkor, ha p>2. Könnyű ellenőrizni, hogy a követelmények minden esetben teljesülnek.

Második feladat. Bebizonyítandó, hogy ha α hegyesszög, akkor
(1+1sinα)(1+1cosα)>5.

 

I. megoldás. A baloldali szorzat
1+1sinα+1cosα+2sin2α
alakban írható, hiszen sinαcosα=12sin2α. Minthogy egy szög szinusza és koszinusza 1-nél nagyobb nem lehet, a felírt összeg második és harmadik tagja legalább 1, utolsó tagja pedig legalább 2. A teljes összeg értéke tehát legalább 5. Az összeg azonban nem lehet 5, mert a két középső tag nem lehet egyszerre 1, hiszen sinα=1 és cosα=1 egyszerre nem teljesülhet. Az összeg értéke eszerint 5-nél nagyobb.
 
II. megoldás. Egy α szögű 1 magasságú derékszögű háromszöget tekintünk (2. ábra) A szögfüggvények értelmezéséből következik, hogy e háromszög befogói és átfogója
a=1cosα,b=1sinα,c=1sinαcosα.
Feladatunk a+b+c>4 bizonyítását kívánja. Ez nyomban következik abból, hogy a+b>c és c≥2, hiszen a derékszögű háromszög magassága az átfogónak legfeljebb a fele, amint ez a Thales-kör szemléletéből is nyomban adódik.
 
 
2. ábra
 

III. megoldás. A feladat állításán túlmenően bebizonyítjuk, hogy ha α hegyesszög, akkor
(1+1sinα)(1+1cosα)≥3+22=5,828...,
s hogy egyenlőség csak az α=45∘ esetben következik be. Ennek igazolásához az I. megoldásra hivatkozva elég belátnunk, hogy
1sinα+1cosα≥22,
s hogy itt is csak α=45∘ esetén következik be az egyenlőség. Ezt háromféleképpen bizonyítjuk be.
a) Az előző megoldás jelöléseit használva a+b≥22 a bizonyítandó állítás. Ez abból adódik, hogy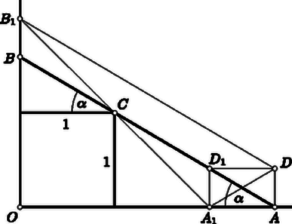
(a+b)2=(a2+b2)+2ab=c2+2cm≥8.
Felhasználtuk itt Pythagoras tételét, a terület kétféle kifejezése alapján adódó ab=cm összefüggést és az m=1 esetben érvényes c≥2 egyenlőtlenséget. Egyenlőség eszerint csak c=2m esetén, azaz egyenlőszárú derékszögű háromszögre következik be.
 
 
3. ábra
 

b) Forgassuk el a 2. ábrában a magasságtól balra elhelyezkedő háromszöget felső csúcsa körül pozitív irányban 90∘-kal. Így a 3. ábra vastagon megrajzolt részéhez jutunk. A bizonyítandó állítás szerint az AB szakasz hosszabb, mint a 45∘-kal hajló A1B1 szakasz, hiszen ennek hossza 22. Azt kell tehát igazolnunk, hogy a derékszögű AOB∢ szárait összekötő s a C ponton áthaladó szakaszok közül a szimmetrikusan elhelyezkedő A1B1 szakasz a legrövidebb.
Minthogy az OA és OB szár között nincs szerepkülönbség, feltehetjük, hogy α<45∘. A B pont C-re vonatkozó tükörképét D1-gyel jelöljük. A C-re vonatkozó szimmetria miatt a BB1, A1D1 szakaszok párhuzamosak és egyenlők. A velük párhuzamos és egyenlő AD szakasz a BADB1 parallelogrammához és az A1ADD1 téglalaphoz vezet. Az utóbbiból kiolvasható, hogy AA1D∢=A1AD1∢=α, és így B1A1D∢=135∘-α>90∘. Eszerint a B1A1D△-ben DB1 a legnagyobb oldal, tehát A1B1<DB1=AB.
c) Felhasználjuk, hogy a pozitív x, y számok a(x,y) számtani, g(x,y) mértani és q(x,y) négyzetes közepére
g(x,y)≤a(x,y)≤q(x,y),
s hogy egyenlőség mindkét esetben csak x=y esetén teljesül. Eszerint
1sinα+1cosα=2a(1sinα,1cosα)≥2g(1sinα,1cosα)==2g(sinα,cosα)≥2q(sinα,cosα)=22.


Egyenlőség csak sinα=cosα, tehát α=45∘ esetén áll fenn.
 

Megjegyzés. A feladatban α hegyesszöget jelentett. Erre a megszorításra azért volt szükség, mert ha 90∘<α<180∘ vagy 270∘<α<360∘, akkor a feladat egyenlőtlenségének a baloldalán csak az egyik tényező pozitív, s a szorzat negatív. Ha viszont 180∘<α<270∘, akkor mindkét tényező negatív, de szorzatuk 1-nél kisebb. Ennek bizonyítását az olvasóra hagyjuk.
 

Harmadik feladat. Bizonyítsuk be, hogy ha a háromszög nem tompaszögű, akkor súlyvonalainak összege nagyobb, mint a háromszög köré írt kör sugarának négyszerese.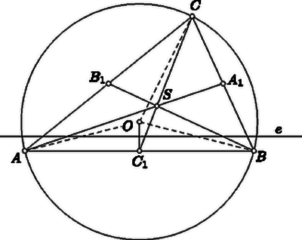
 
Megoldás. Ha az ABC△ nem tompaszögű, akkor (a belsejében vagy a határán) tartalmazza a köréírt kör O középpontját. Ezért az S súlypont által meghatározott SAB, SBC, SCA háromszögek közül legalább az egyik szintén tartalmazza az O pontot. Legyen az SAB△ ilyen (4. ábra).
 
 
4. ábra
 

Minthogy az SAB△ tartalmazza az OAB△-et,
SA+SB≥OA+OB,
és az egyenlőség csak akkor teljesülhet, ha O és S azonos. Eszerint az sa=AA1, sb=BB1 súlyvonalakra és a körülírt kör r sugarára
23sa+23sb≥2r,
vagyis
sa+sb≥3r.

Ha O azonos C1-gyel, akkor nyilván CO=CC1. Ha azonban O nem azonos C1-gyel, akkor az OC1 szakaszt merőlegesen felező e egyenes belevág a háromszögbe, tehát a vele párhuzamos AB szakaszt elválasztja a C csúcstól. Eszerint C és O ugyanabban az e egyenes által határolt félsíkban van, s ezért a C pont az e egyenesre vonatkozólag szimmetrikusan elhelyezkedő O, C1 pontok közül O-hoz van közelebb. A CC1=sc, és CO=r szakaszokra ezek szerint
sc≥r
mindig teljesül, és egyenlőség csak akkor áll fenn, ha O és C1 azonos.
Egyenlőtlenségeinket összeadva
sa+sb+sc≥4r
adódik, de itt az egyenlőség soha sem teljesülhet, mert egyszerre nem teljesülhet mind a két összeadott egyenlőtlenségben, hiszen O nem lehet az egymástól különböző S, C1 pontok mindegyikével azonos.
 

Megjegyzések. 1. Nem hagyható el a feladatnak az a megszorítása, hogy a háromszög nem tompaszögű. Bármilyen csekély túllépést engednénk is meg 90∘ fölé, a feladat állítása már nem volna helyes. Bebizonyítjuk, hogy ez valóban így van.
Induljunk ki tehát egy tetszőlegesen megadott ABC∢>90∘ szögből. Messe az AB=c szakasz felezőmerőlegese a BC szárra B-ben emelt merőlegest az O1 pontban (5. ábra). A BC száron úgy választjuk meg a C pontot, hogy a BC=a távolságra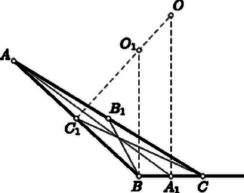
a+c≤2⋅BO1
teljesüljön. Az ABC△ köré írt kör sugarára
r=BO>A1O>BO1,
hiszen a két utolsó szakasz ugyanannak a szögnek párhuzamos szelője, és BO1 van a szög csúcsához közelebb.
 
 
5. ábra
 

Az ABC△ súlyvonalaira az ABA1, BC1B1, CBC1 háromszögek egyenlőtlenségei alapján
sa<a2+c,sb<a2+c2,sc<a+c2.
Ezek szerint
sa+sb+sc<2(a+c)<4⋅BO1<4r.

 

2. Bebizonyítjuk, hogy akkor sem volna helyes a feladat állítása, ha benne 4 helyett valamely 4-nél bármi csekéllyel is nagyobb szám állna.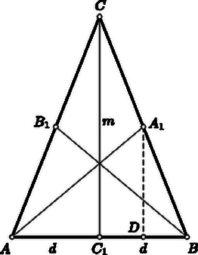
 
 
6. ábra
 

Egy 2d alapú, m magasságú egyenlőszárú háromszög (6. ábra) súlyvonalaira az AA1D△-re vonatkozó egyenlőtlenség felhasználásával
sa=sb<m2+32d,sc=m,sa+sb+sc<2m+3d.


A körülírt kör sugarára
r>m2,
hiszen az m magasságot a kör tartalmazza. Ezek szerint
sa+sb+sc<(4+6dm)r.
Ha λ egy tetszőleges, 4-nél nagyobb szám, m rögzítése után d megválasztható olyan kicsire, hogy
4+6dm<λ
teljesüljön. Az így adódó háromszögre a fentiek szerint
sa+sb+sc<λr.

3. A feladat arról szólt, hogy a súlyvonalak összege a körülírt kör sugarának legalább hányszorosa. Bebizonyítjuk most, hogy legfeljebb 4,5-szöröse, és itt a háromszöget illetően semmiféle megszorítást sem teszünk. Szabályos háromszög esetében a vizsgált arány éppen 4,5. Meglepő talán a nem tompaszögű háromszögekre érvényes viszonylag szűk (4, 4,5) értékköz.
Tekintsük a sík egy P pontjának az ABC△ csúcsaitól mért távolságait. Ezek számtani közepét a(P), négyzetes közepüket pedig q(P) jelöli. Ismeretes, hogy a(P)≤q(P).
Bizonyításunk arra épül, hogy q(P)≥q(S). Ha az A, B, C pontokba egységnyi tömegeket helyezünk, akkor 3[q(P)]2 e tömegrendszer tehetetlenségi nyomatéka a síkot a P pontban merőlegesen döfő egyenesre vonatkozólag. Az imént kimondott egyenlőtlenség következik tehát abból, hogy párhuzamos tengelyek közül a súlyponton áthaladó tengelyre vonatkozó tehetetlenségi nyomaték a legkisebb.
Egyenlőtlenségünket fizikai ismeretekre való hivatkozás nélkül akarva bebizonyítani bevezetjük az
SA→=a,SB→=b,SC→=c,SP→=p

vektorokat (lásd pl. Matematikai Versenytételek, II. rész, 26‐30. o. és 69. o.). Felhasználjuk azt, hogy
a+b+c=0.
Az egyenlőtlenségünkben szereplő értékekre
3[q(S)]2=a2+b2+c2,3[q(P)]2=(a-p)2+(b-p)2+(c-p)2==(a2+b2+  c2)-2p(a+b+c)+3p2==3[q(S)]2+3p2≥3[q(S)]2.
Ezzel a q(P)≥q(S) egyenlőtlenség bizonyítást nyert, de ebből eredeti állításunk is nyomban következik:
sa+sb+sc=92a(S)≤92q(S)≤92q(O)=92r.

 

4. Megemlítjük, de nem részletezzük, hogy a tetraéder súlyvonalainak összege a körülírt gömb sugarának legfeljebb 16/3-szorosa, s hogy ez ugyanúgy bizonyítható, ahogyan a megfelelő síkbeli állítást éppen bebizonyítottuk.
Ha feladatunk állításának térbeli megfelelőjét keressük, valamilyen megszorítást kell tennünk a tetraéderre vonatkozólag, annak megfelelően, hogy a feladat csak nem tompaszögű háromszögekről szólt. Azok a háromszögek nem tompaszögűek, amelyek tartalmazzák a köréjük írt kör középpontját. Érthető tehát, hogy azokról a tetraéderekről szólunk, amelyek tartalmazzák a köréjük írt gömb középpontját, azonban csak bizonyítás nélkül említjük meg, hogy az ilyen tetraéderek súlyvonalainak összege a körülírt gömb sugarának 4-szeresénél nagyobb, és itt 4 helyébe nagyobb számot írva már helytelen állításhoz jutunk.
 
 Hajós György