Cím: Az 1963. évi Arany Dániel tanulóversenyek II. fordulóján kitűzött feladatok megoldása: Kezdők (I. osztályosok) versenye
Szerző(k):  Fried Ervin 
Füzet: 1964/február, 49 - 51. oldal  PDF  |  MathML 
Témakör(ök): Arany Dániel

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

1. feladat. Szerkesszünk háromszöget, ha adott egy szöge, az ezt bezáró oldalak különbsége és a szög csúcsából kiinduló súlyvonal hossza.

 
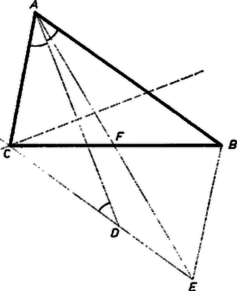
Megoldás. Készítsünk vázlatot, legyen ABC a keresett háromszög, az A csúcsnál levő α szög, az onnan induló sa súlyvonal és az A-ból kiinduló két oldal különbsége adottak. Jelöljük A-nak a BC oldal F felezőpontjára való tükörképét E-vel. Az ABEC négyszög paralelogramma, amelyben ismertek a szögek (az A-nál és E-nél levő α, a B-nél és C-nél levő 180∘-α), az AE átló (2sa) és a szomszédos oldalak különbsége. Az ACE háromszöget tekintve, abban ismert az AE oldal, a szemközti szög és az azt bezáró oldalak különbsége, így megszerkesztése a tankönyvből ismert alapfeladat: rámérve CE-re a CD=CA szakaszt az ACD háromszög egyenlő szárú, amiből ADE∢=180∘-α/2 adódik, ismert továbbá az ADE háromszögben két oldal: DE (a különbség) és AE=2sa.
 
 

Ezek után a szerkesztés menete a következő: Az előírt különbséggel egyenlő hosszú DE szakaszt húzunk, ezzel D-ben 180∘-α/2 szöget bezáró félegyenest szerkesztünk és ezt elmetsszük az E középpontú, 2sa sugarú körívvel: a metszéspont legyen A. Megszerkesztjük az AD szakasz felező merőlegesének és az ED egyenesnek C metszéspontját; végül vesszük C-nek az AE szakasz F felezőpontjára való B tükörképét.
Az ABC háromszög megfelel a feltételeknek. Ugyanis a tükrözés miatt F felezi a BC szakaszt, tehát AF az ABC háromszög súlyvonala, másrészt hossza sa. Az ECAB négyszög paralelogramma, AB párhuzamos CD-vel, ezért a BAD és CDA szögek egyenlők, ugyanis váltószögek, továbbá DAC∢=CDA∢, mert az ACD háromszög egyenlő szárú, így pedig BAC∢=BAD∢+DAC∢=2CDA∢=α. Végül AB-AC=CE-CA=CE-CD=DE, az előírt hosszúság.
Minthogy nyilvánvalóan 0∘<α<180∘, azért ADE∢=180∘-α/2>90∘, tehát ez a szög az ADE háromszög legnagyobb szöge. Így az ADE háromszög szerkeszthetőségének feltétele, hogy AE>ED legyen, azaz a keresett háromszög súlyvonalának kétszerese nagyobb legyen a szöget bezáró oldalak különbségénél. Másrészt α/2 hegyesszög, azért C mindenesetre létrejön éspedig valóban DE-nek D-n túli meghosszabbításán, amint a különbség képezésében felhasználtuk. Végül B mindig létrejön, ezért a feladatnak a mondott feltétel teljesülése esetén 1 megoldása van.
 
2. feladat. Egy papírra többjegyű számok vannak írva. Ezek közül kihúzzuk azokat, amelyeknek az utolsó jegyük páratlan, de az utolsó előtti páros, továbbá azokat, amelyeknek az utolsó jegye páratlan és 3-mal nem oszthatók, valamint azokat is, amelyeknek utolsó előtti jegye páratlan és 3-mal oszthatók. Bizonyítsuk be, hogy így a papíron csupa páros szám maradt.
 
Megoldás. Tudjuk, hogy egy szám aszerint páros vagy páratlan, amint utolsó jegye páros vagy páratlan. Így, ha maradnak az első lépés után a papíron páratlan számok, akkor azoknak már az utolsó két jegye páratlan. Ezek közül a 3-mal nem oszthatókat kihúzzuk a második alkalommal, a 3-mal oszthatókat pedig a harmadik alkalommal. Így egyetlen páratlan szám sem marad a papíron, és ezt kellett bizonyítani.
 
Megjegyzések. 1. Az utolsó lépésben esetleg páros számokat is kihúztunk, ez azonban kérdésünk szempontjából lényegtelen.
 
2. A 3-mal való oszthatóság helyett mondhatnánk bármilyen más tulajdonság nem teljesülését, ill. teljesülését a második, ill. harmadik kihúzási előírásban.
 
3. Még általánosabban a ,,párosnak lenni'', ,,páratlan utolsó előtti jeggyel rendelkezni'' és ,,hárommal oszthatónak lenni'' tulajdonságokat tetszés szerinti P, U és H tulajdonsággal helyettesítve, a papírra írt számokat pedig tetszés szerinti olyan elemekkel, amelyek rendelkezhetnek ezekkel a tulajdonságokkal ‐ igaz marad, hogy elhagyva az elemek közül a P és U tulajdonságokkal rendelkezőket, továbbá azokat, amelyeknek megvan a P tulajdonságuk, de H nincs meg, végül azokat is, amelyeknek megvan a H tulajdonságuk, de U nincs meg ‐, csupa a P tulajdonsággal nem rendelkező elem marad vissza. Az olvasóra bízzuk a fönti megoldás átírását a most megfogalmazott állítás esetére.
 
3. feladat. Bizonyítsuk be, hogy ha egy k-jegyű szám négyzete ugyanazzal a k jeggyel kezdődik, akkor ez a szám tíznek hatványa.
 
I. megoldás. Legyen N olyan k-jegyű egész szám, melynek négyzetében az első k jegy rendre megegyezik N jegyeivel. Ekkor az N2:N osztás N-et, tehát egy k-jegyű számot ad hányadosul. Másrészt a szokásos módon végezve az osztást az első részletosztandó, N2 első k jegye éppen N; ebben az osztó megvan 1-szer, az első részletmaradék pedig 0. A hányados első jegye tehát 1, és az N2 osztandó további jegyeit egyenként sorra ,,levéve'' a hányados további jegyei gyanánt mindaddig 0-t kapunk, amíg a részletosztandók k-nál kevesebb jegyűek, tehát k-1 egymás utáni lépésben. Így a hányados kezdő 1-ese után k-1 db 0 jegy következik. Ezzel viszont megkaptuk az N hányadosnak mind a k jegyét, tehát N valóban 10-nek hatványa: 10k-1, ennélfogva N2=102k-2, vagyis az osztás összes lépéseiben 0 a maradék.
 
II. megoldás. Legyen ismét N a kérdéses alapszám, és tegyük fel, hogy N2-ben az N jegyeivel rendre megegyező első k számjegy után még t darab számjegy szerepel. Mindezeket zérussal helyettesítve (ha nem eredetileg azok), N-nek 10t-szeresét kapjuk, és N2 nagyobb a kapott számnál, vagy éppen egyenlő vele:
N2≥N⋅10t.
Ezt (a pozitív) N-nel osztva
N≥10t.(1)
Írjunk másrészt N2 összes további jegyei helyére 9-eseket. A kapott szám N⋅10t-nél a t jegyből álló 999...9=10t-1 számmal nagyobb, másrészt N2 kisebb ennél a számnál, vagy éppen egyenlő vele:
N2≤N⋅10t+10t-1=(N+1)10t-1.
A jobb oldal 1-gyel kisebb N+1-nek 10t szeresénél, a bal pedig 1-gyel nagyobb az (N+1)(N-1)=N2-1 számnál, így
N2-1<(N+1)10t.
Ezt (a pozitív) N+1-gyel osztva
N-1<10t,N<10t+1.
Eredményünket (1)-gyel egybevetve N=10t, hiszen N egész szám. Ezzel az állítást bebizonyítottuk. Mivel N k-jegyű, azért t=k-1.
 
Megjegyzések. 1. Megoldásainkban feltettük, hogy egész számról van szó. Valóban csak ezeknél szoktunk a számjegyek számáról beszélni. Tizedes jegyek után tetszés szerinti számú 0-t írhatunk, s így a számjegyek száma határozatlan. Ha N és N2 tizedes jegyeket is tartalmaznak, 10 alkalmas hatványával szorozva visszavezethetjük a kérdést egész számokra.
 
2. A feladat állítása 2-nél nagyobb hatványkitevő esetén nem igaz. Pl. 323=32768, a számjegyek sorozata szintén 32-vel kezdődik, vagy 464164=4641633499322843136, 185=1889568, 166=16777216; 177835 kezdő számjegyei ugyancsak 1, 7, 7, 8, 3. Az I. megoldás gondolatmenete rámutat ennek lehetőségére. Pl. N3:N=N2 jegyeinek száma több, mint k, tehát a hányadosban a k+1-edik helytől kezdve már felléphet 0-tól különböző számjegy.
 Fried Ervin