Cím: Az 1963. évi Arany Dániel tanulóversenyek II. fordulóján kitűzött feladatok megoldása: Haladók (II. osztályosok) versenye
Szerző(k):  Lőrincz Pál 
Füzet: 1964/január, 1 - 5. oldal  PDF  |  MathML 
Témakör(ök): Arany Dániel

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

1. feladat. Adva van a síkban három különböző pont, K, L és M. Tekintsük mindazokat az egyenlő szárú derékszögű háromszögeket, melyeknek oldalegyenesei rendre átmennek az adott pontokon úgy, hogy az átfogó oldalegyenese az M ponton menjen át. Mi a mértani helye e háromszögek köré írható körök középpontjainak?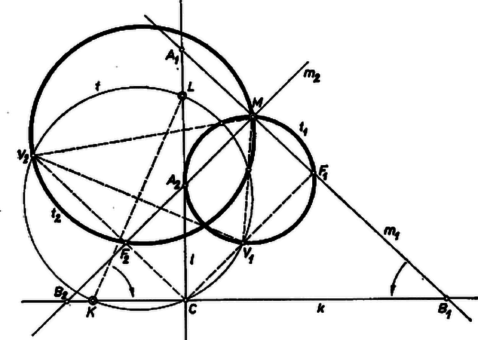

 
 

Megoldás. A keresett mértani hely egy pontját a következőképpen szerkeszthetjük meg. Húzunk egy tetszőleges k egyenest a K ponton át, majd L-en át egy erre merőleges l egyenest, metszéspontjuk legyen C. Ezután az M ponton keresztül meghúzzuk a k-val 45∘-os szöget bezáró m1, m2 egyeneseket. Az ábrán m1 az óramutató járásával ellenkező irányban 45∘-kal elforgatva jut k-ra, m2 pedig megegyező irányú 45∘-os forgatással. Messe k-t és l-et m1 a B1, ill. A1 pontban, m2 pedig B2-ben, ill. A2-ben. Ekkor A1B1C és A2B2C a feladat követelményeinek megfelelő egyenlő szárú derékszögű háromszögek. A derékszögű háromszög köré írt kör középpontja az átfogó felezőpontja, ábránkon A1B1 felezőpontja F1, A2B2 felezőpontja F2, mindkettő hozzátartozik a keresett mértani helyhez.
Azt keressük, milyen alakzatot ír le F1 és F2, míg k a K körül ‐ s így l az L körül, m1 és m2 pedig az M körül ‐ egyszer körülfordul.
Az átfogók felezőpontjait A1 és B1, ill. A2 és B2 kijelölése nélkül is megkaphatjuk, ugyanis C a KL szakasz fölé írt t Thalesz‐körön van, CFi pedig (i=1, 2) ‐ egyenlő szárú háromszögről lévén szó ‐ felezi az AiCBi szöget és merőleges mi-re, tehát Fi-t M merőleges vetülete adja a k, l egyenespár megfelelő fi szögfelezőjén. E szögfelezők minden helyzetben felezik t-nek a szárak közé eső KL félkörívét is, és így átmennek t-nek a KL-re merőleges V1V2 átmérője valamelyik végpontján (az ábrán CF1 átmegy V1-en, CF2 pedig V2-n. Ezért ‐ bármilyen is a C, Fi, Vi pontok sorrendje ‐, mindig fennáll: MF1C∢=MF1V1∢=90∘ és MF2C∢=MF2V2∢=90∘. Így a k különböző helyzeteihez tartozó F1 pontok a V1M, mint átmérő fölé rajzolt t1 Thalesz‐körön vannak, az F2 pontok pedig a V2M átmérő fölé rajzolt t2 Thalesz‐körön.
Hátra van még annak megvizsgálása, hogy a két utóbbi Thalesz‐kör minden pontja hozzátartozik-e a mértani helyhez. Legyen a t1 kör egy M-től és V1-től különböző pontja X1, és kössük össze X1-et V1-gyel és M-mel. Ekkor MX1V1∢=90∘; továbbá, miután V1 rajta van a t körön, az X1V1 egyenes e kört általában még egy C pontban metszi. Így a CK, CL és X1M egyenesek egy derékszögű egyenlő szárú háromszöget alkotnak, és e háromszög köré írt kör középpontja éppen a felvett X1 pont. Ugyanis a CX1 és CK egyenesek kisebbik szöge 45∘, mert az egyenesek között t-nek valamelyik V1K íve fekszik, vagyis a kör negyede vagy háromnegyede, így a CK-ra merőlegesen álló CL egyszersmind tükrös párja is CK-nak CX1-re, továbbá X1M önmagának tükörképe CX1-re, hiszen merőleges rá; végül X1 az így nyert háromszög átfogójának és szimmetriatengelyének közös pontja. ‐ X1 gyanánt V1 is vehető, ekkor X1V1 egyenes gyanánt az X1M=V1M átmérőre emelt merőleges, t1-nek V1-beli érintője veendő, hasonlóan X1=M esetén az M-beli érintőt vesszük X1M gyanánt. ‐ Hasonlóan előfordulhat, hogy X1V1 a t kört másodszor éppen K-ban, vagy L-ben metszi, ekkor az egyik befogó egyenese a KL egyenes, a másiké pedig a talált metszéspontban t-hez húzott érintő. C gyanánt adódhat maga V1 is, ha ti. X1V1 éppen érinti a t kört.
Ezzel bebizonyítottuk, hogy a t1 kör minden pontja a mértani helyhez tartozik. Hasonlóképpen az F2 pontok t2 körének minden pontja ugyancsak hozzátartozik a mértani helyhez, mert meggondolásaink V1 helyén V2-vel változatlanul érvényesek. A keresett mértani hely tehát a t1 és t2 körökből áll.
 
Megjegyzés. Lehetséges, hogy az ABC egyenlő szárú derékszögű háromszög ponttá zsugorodik össze, éspedig akkor és csak akkor, ha C azonosnak adódik X1-gyel, hiszen a szóban forgó körülírt kör sugara X1C. Ilyen X1 mindig van: t és t1-nek V1-től különböző közös pontja, ill. ha t és t1 érintkeznek, akkor maga V1.
 

2. feladat. Egy tört számlálója és nevezője egyaránt kétjegyű egész szám, és a számláló tízeseinek a száma egyenlő a nevező egyeseinek számával. Elhagyva a közös jegyet, a megmaradt egyjegyű számok hányadosa egyenlő az eredeti tört értékével. Melyik ez a tört?
 

Megoldás. A feladat olyan a, b, c számjegyek keresését kívánja, amelyekre
10a+b10c+a=bc.
Itt a és c nem 0, mert a bal oldal kétjegyű számok hányadosa, de b sem lehet 0, mert akkor a jobb oldal 0, tehát a=0 kellene hogy legyen. A törteket eltávolítva
10ac+bc=10bc+ab,
amit, a 10-zel szorzott tagokat egy oldalra rendezve, így írhatunk:
10(a-b)c=(a-c)b.(1)
Itt, ha a-b nem 0, akkor vagy a-c egyenlő 5-tel, vagy -5-tel, vagy b=5, mert mindkét tényező abszolút értéke kisebb 10-nél.
 

1) Ha a-b=0, akkor a-c=0, vagyis a=b=c, és ez nyilván minden pozitív a számjegyre megoldása a feladatnak.
 

2) Ha a-c=-5, a=c-5, akkor (1)-ből (-5-tel egyszerűsítve)
2(b+5-c)c=b.
Ha c≤5, akkor a bal oldal nagyobb, mint b, ha pedig c>5, akkor a bal oldal 10-nél nagyobb, tehát nem lehet egy számjeggyel egyenlő.
 

3) Ha a-c=5, a=c+5, akkor (1)-ből
2(c+5-b)c=b,(2c+1)b=2c(c+5).
Innen
b=c+5-c+52c+1=c+5-2c+1+92(2c+1)=c+92-92(2c+1).
Ez csak úgy adhat egész számot, ha 2c+1 osztója a 9-nek. Ez c=1, 4 esetekben következik be. Ekkor b értéke 4, ill. 8, a=c+5 értéke pedig 6, ill. 9. Az ezekkel felírt törtek
6416=41,9849=84
valóban megfelelnek a feladat követelményeinek.
 

4) Végül, ha b=5, (1)-ből
2(a-5)c=a-c,(2c-1)a=9c.
Ebből
a=9c2c-1=92+92(2c-1).
Ez akkor pozitív egész, ha 2c-1 a 9 pozitív osztója, tehát c=1, 2, 5. Az a-ra adódó értékek 9, 6, 5. Ezek közül a harmadik értékhármas az 1) alatt szerepelt megoldások egyikét adja, a másik kettőhöz tartozó törtekre
9519=51,6526=52,
tehát ezek is megfelelnek a feladat követelményeinek; így 9 érdektelen megoldás mellett további 4 megoldása van a feladatnak.
 

Megjegyzések. Több versenyző a követelmény alapján kifejezte valamelyik számjegyet a másik kettővel, majd az utóbbiak minden lehetséges értékpárja mellett azt vizsgálta, lehet-e számjegy a kifejezés értéke. Látjuk, hogy a feladat kevesebb próbával is megoldható. Számosan egy megfelelő számjegyhármas megtalálása után abbahagyták a próbálgatást.
 

3. feladat. Oldjuk meg a következő egyenletrendszert:
x2-xy+y2=2,(1)x3-y3=4.(2)



Megoldás. Alkalmas új ismeretlenek bevezetése útján feladatunkat egyszerűbb egyenletekből álló egyenletrendszer megoldására vezethetjük vissza. Legyen pl.
x-y=u,ésxy=v,
akkor egyenleteink így alakulnak át:
x2-xy+y2=(x-y)2+xy=u2+v=2,(1a)x3-y3=(x-y)3+3xy(x-y)=u3+3uv=4.(2a)


Az első egyenletből v kifejezését a másodikba helyettesítve:
u3+3u(2-u2)=4.
Rendezés és egyszerűsítés után a bal oldalt szorzattá alakíthatjuk:
u3-3u+2=0,(u3-u)-2(u-1)=(u-1)[u(u+1)-2]=(u-1)(u2+u-2).


Ez a szorzat akkor és csak akkor 0, ha valamelyik tényezője 0, tehát vagy u-1=0, u1=1, vagy u2+u-2=0. Az utóbbi egyenlet két gyöke u2=1 és u3=-2. Az u-khoz tartozó v-ket az (1a) egyenletből számíthatjuk ki,
v1=1,v2=1,v3=-2.
Az u1=1, v1=1 gyökrendszerhez tartozó x és y értékeket az
u=x-y=1,v=xy=1
egyenletekből kiszámítva
x1=5+12,y1=5-12;x2=-5-12,y2=-5+12.


Az u2, v2 gyökpárból nem kapunk új megoldást. Az u3=-2, v3=-2 gyökpárral adódó x-y=-2, xy=-2 egyenletrendszernek nincs valós megoldása.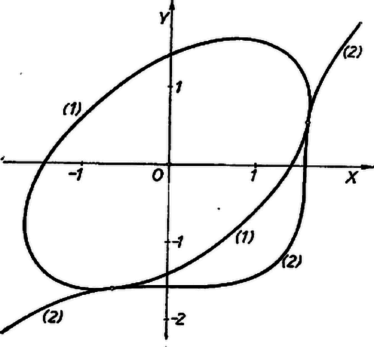
 
 

Megjegyzés. Bizonyítás nélkül megemlítjük, hogy (1) képe a derékszögű koordinátarendszerben olyan ellipszis, amelynek középpontja az origó, szimmetria tengelyei a koordináta‐tengelyekkel 45∘-os szöget zárnak be, nagy tengelye az I. és III. síknegyedekben halad, (2) képe pedig egy ún. harmadrendű görbe. A mindkét egyenletet kielégítő x, y számpárokhoz tartozó pontok a görbéknek közös pontjai, ez esetben érintkezési pontok, bennük a két görbének közös az érintője is.