Cím: Váltóáramú ellenállások tárgyalása komplex számokkal
Szerző(k):  Károlyi Géza ,  Török Sándor 
Füzet: 1963/november, 161 - 164. oldal  PDF  |  MathML 
Témakör(ök): Szakmai cikkek

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Középiskolában ‐ gimnáziumban és technikumokban ‐ a fizika tanítása során mind a tananyag feldolgozásában, mind pedig a feladatok megoldásában számos lehetőség adódik a fizika‐anyag és a tanult matematikai anyag összekapcsolására. A tananyag feldolgozásában főleg kísérleti, induktív módszerrel jutunk el a keresett mennyiségi összefüggésekhez, törvényekhez. Sok esetben a kísérletek alapján megállapított összefüggések jobb megértését segíti elő a tanult matematikai anyaggal való összekapcsolás.
Az elektromosságtan tárgyalása közben megismerkedünk a váltóáramú ellenállásokkal. Ebből a tárgykörből a következőkben egy olyan kísérletet írunk le, amelynek algebrai megoldása szükségessé teszi a komplex számok fogalmának ismeretét. A komplex számokkal való elemi műveletek részletes ismertetésére nem térünk ki, mert ez Rieger Richárd: ,,A komplex számok'' c. középiskolai szakköri füzetben megtalálható.
Két, dobozba zárt elektromos fogyasztót sorbakapcsolunk, és 50 Hz-es 200 voltos váltakozó árammal tápláljuk őket. Az áramkörbe bekötött árammérő műszer 100 mA-t mutat. Ezek után kapcsoljuk a két fogyasztót párhuzamosan, ugyanazzal az áramforrással táplálva az árammérő ismét 100 mA-t mutat. Hogyan lehetséges ez? Azt várnánk, hogy párhuzamos kapcsolás esetén, mivel az ellenállás csökken, az áramerősség (J) megnő; ellentmondást látunk a tanult anyag és a kísérlet eredménye között. Mi lehet az oka ennek a ,,látszólagos'' ellentmondásnak? A matematika segítségével könnyen megmagyarázhatjuk kísérletünk eredményét a következő módon.
Jelölje X1 az egyik, X2 pedig a másik fogyasztó ellenállását. Az eredő ellenállás pedig legyen R, mindkét esetben (I=100 mA és U=200 V miatt) ugyanaz. Ezután felírhatjuk a jól ismert összefüggéseket.

X1+X2=R,(1)1X1+1X2=1R.(2)


A (2) egyenletből
R=X1⋅X2X1+X2.
A nevező helyett R is írható. Ekkor
R=X1⋅X2R,vagyR2=X1⋅X2.
A két egyenletünk ezek után:
X1+X2=R(3)X1⋅X2=R2.(4)


Az eddigi eredményt aránylag egyszerű módon szóban így fogalmazhatjuk meg.
Melyik az a (X1 és X2) két szám, amelyeknek összege R, szorzata pedig R2? Ha pl. R=10, akkor azonnal látszik, hogy a valós számkörben ilyen számok nem lehetnek. Ugyanis, ha a két szám összege 10, az adott számok csakis 10-nél kisebb pozitív számok lehetnek. Viszont két 10-nél kisebb pozitív szám szorzata 100 nem lehet. (R2=100.)
Ezek után oldjuk meg a fenti egyenletrendszert. (3)-ból
X2=R-X1,
ezt helyettesítsük (4)-be, ekkor kapjuk, hogy
R2=X1(R-X1),továbbáR2=RX1-X12;rendezveX12-RX1+R2=0.
A megoldás
X1=R+R-32ésX2=R-R-32.
Mivel a gyökjel alatt negatív szám van, az egyenlet gyökei nem lehetnek valósak. Ha bevezetjük az immaginárius egységet, -1-et, melyet az elektromosságtanban j-vel jelölünk, akkor a megoldás így írható:
X1=R2+jR23,(5)
és hasonlóképpen
X2=R2-jR23.(6)
Ezzel kimutattuk, hogy az egyenletrendszer gyökei komplex számok. Visszatérve kísérletünk megfogalmazásához, ez azt jelenti, hogy mindkét fogyasztóban ugyanolyan R2 ohmikus ellenállás van, amely az egyikben +jR23 induktív, a másikban pedig -jR23 kapacitív ellenállással van sorbakötve. Tehát az egyik dobozban (fogyasztóban) R/2 ohmos ellenállás és egy tekercs, a másikban pedig R/2 ohmos ellenállás és egy kondenzátor van sorbakötve. Elektrotechnikában az induktív ellenállás szimbólikus alakja: jωL, a kapacitív ellenállásé pedig: -j1ωC. Az ohmos ellenállást a valós tengelyen, az induktív ellenállást a pozitív imaginárius, a kapacitív ellenállást pedig a negatív imaginárius tengelyen ábrázoljuk. Az ellenállásokat vektoriálisan összegezzük. Példánkban az induktív és kapacitív ellenállás abszolút értékét tekintve megegyezik egymással.
 
Az előbbiek szerint a +jR23 számnak megfelel az ωL induktív ellenállás, és -jR23 számnak megfelel az 1ωC kapacitív ellenállás.
Az eddig elmondottakat szemléletesebbé tehetjük, ha a számítás eredményeit grafikusan is bemutatjuk. Jól tudjuk, hogy az R23 egy olyan egyenlőoldalú háromszögnek magassága, amelynek az oldala R. Ennek az ismeretében pontosan megszerkeszthetjük minden esetben az eredő ellenállást.
Az egyik fogyasztó esetében: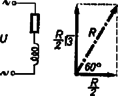
 
 
1. ábra
 

A másik fogyasztó esetében: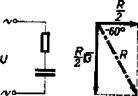
 
 
2. ábra
 


Ebből láthatjuk, hogy akkor is 100 mA az áramerősség, ha csak az egyik fogyasztót kapcsoljuk be a váltóáramú áramforrásba. Az első esetben cosφ=+1/2, a második esetben szintén cosφ=+1/2.
Ha a két fogyasztót sorbakapcsoljuk és így kötjük be az áramkörbe (3. ábra), akkor az eredő 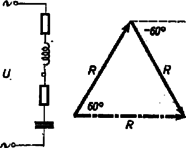R, és a cosφ=1, azaz φ=0.
 
 
3. ábra
 

Ha a két fogyasztót párhuzamosan kötjük, és így kapcsoljuk be az áramkörbe (4. ábra), akkor az eredő ellenállás szintén 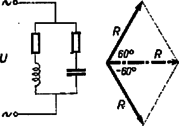R, és cosφ=1, azaz φ=0.
 
 
4. ábra
 

Ezzel igazoltuk, hogy a mérésekből adódó ellentmondás csak látszólagos. A mérést helyesen végeztük, és mindenkor ugyanilyen eredményre jutunk, ha az egyik fogyasztóban ohmikus és induktív, a másik fogyasztóban pedig ohmikus és kapacitív ellenállás van sorbakapcsolva. (Természetesen akkor, ha az ellenállásértékek megfelelőek.)
Ha az ohmikus ellenállást adottnak vesszük, könnyen kiszámíthatjuk, hogy milyen tekercsre, illetve milyen kondenzátorra van szükségünk a fenti kísérletnél. Ha U=200 V, I=100 mA, akkor R=2000Ω. Ennek ismeretében a tekercs önindukciós együtthatója: ωL=R23, ωL=1730Ω, L=1730314=5,5 H; a kondenzátor kapacitása: 1ωC=1730Ω, C=1ω⋅1730 F, C=106314⋅1730=1,84μF.
Eredményül kaptuk, hogy az 1000Ω-os ellenállással az egyik dobozban egy 5,5 H önindukciós tényezőjű tekercs, a másik dobozban pedig egy 1,84μF kapacitású kondenzátor van sorbakötve.
A kísérlet és a számítás eredményének megegyezésével igazoltuk, hogy sok esetben, amikor a kísérleti eredményben ,,ellentmondást'' látunk, a matematika alkalmazásával milyen könnyen feloldhatjuk az ellentmondásokat. Úgy gondoljuk, hogy az itt ismertetett módszernek szakköri foglalkozáson való feldolgozása élményt jelent, mert megismerkedünk a komplex számok alkalmazhatóságával, és meggyőződünk róla, hogy milyen hasznos a váltóáramú ellenállásoknak komplex számokkal való tárgyalása.
 
Török Sándor és Károlyi Géza