Kezdőlap


Cím:	1963. évi fizika OKTV feladatai
Füzet:	1963/október, 81 - 88. oldal	PDF \| MathML
Témakör(ök):	OKTV

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Az I. forduló feladatai:

1. A Föld felszínétől mérve mekkora magasságban kering az a mesterséges hold, amelynek keringési ideje

90

perc? A Földet gömbalakúnak tekintve, sugarát

6370 km

-nek vesszük és a Föld felszínén mért nehézségi gyorsulást ismertnek tételezzük fel

(g_{0} = 981 {cm/sec}^{2})

. A mesterséges hold körpályán kering.

Megoldás: A mesterséges hold centripetális gyorsulása egyenlő a tömegvonzási erőből származó gyorsulással:

ω^{2} r = \frac{f M}{r^{2}}

. Itt

f

gravitációs állandó és

M

a Föld tömege,

ω

pedig a szögsebesség, amely a mi esetünkben

ω = \frac{2 π}{T} = \frac{2 π}{5400 sec} = 1, 164 \cdot 10^{- 3} {sec}^{- 1}

; a körpálya rádiusza

r

. A mesterséges hold körpályájának rádiusza:

\begin{matrix} r = \sqrt[3]{\frac{f M}{ω^{2}}} . \end{matrix}

A Föld felszínén a középponttól

r_{0}

távolságban a nehézségi gyorsulás

g_{0} = \frac{f M}{r_{0}^{2}}

, vagyis

f M = g_{0} r_{0}^{2}

. Ezzel a körpálya rádiusza

r = \sqrt[3]{\frac{g_{0} r_{0}^{2}}{ω^{2}}}

. Számadatainkat felhasználva

r = 6650 km

és a Föld felszíne feletti magasság

r - r_{0} = 6650 - 6370 = 280 km

2. Az ábra szerinti kapcsolás esetén, ha

R

ellenállások értéke egyenlő, akkor a főágban

I

erősségű áram folyik. Hányszorosára változik ez az áram, ha két, átellenesen fekvő ellenállás értékét megkétszerezzük?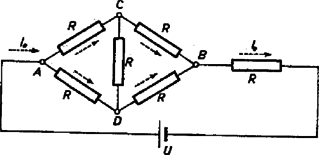

1. ábra

Megoldás: Az 1. ábra szerint

C

és

D

pontok feszültsége egyenlő, ezért a közöttük levő, átlósan fekvő ellenállást kiiktathatjuk. Az

A C B

darab, valamint az

A D B

darab ellenállása

2 R

, azonban a két párhuzamosan kapcsolt

2 R

eredője

R

, amely sorba van kapcsolva a különálló

R

ellenállással. Így az egész áramkör ellenállása

2 R

és az áramerősség: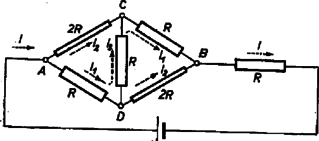

\begin{matrix} I_{0} = \frac{U}{2 R} . \end{matrix}

2. ábra

A 2. ábra szerint a teljes

I

áramerősség

I_{1}

és

I_{2}

részre oszlik szét

A

pontban. Jelen esetben

D

és

C

feszültsége eltérő, ezért

D

és

C

között levő ellenálláson

I_{3}

áram folyik. A feszültségesés

A

-tól

C

-ig ugyanannyi, mint

A D C

úton:

2 R I_{2} = R I_{1} + R I_{3}

, illetve

\begin{matrix} 2 I_{2} = I_{1} + I_{3}; \end{matrix}

továbbá felírjuk az áramelágazás követelményét

A

-ban és

D

-ben:

\begin{matrix} I = I_{1} + I_{2}, I_{1} = I_{2} + I_{3} . \end{matrix}

Három egyenletünket megoldjuk

I_{1}

I_{2}

és

I_{3}

-ra; az eredmény:

\begin{matrix} I_{1} = \frac{3}{5} I, I_{2} = \frac{2}{5} I, I_{3} = \frac{1}{5} I . \end{matrix}

Az egész feszültségesés

A

és

B

között:

2 R I_{2} + R I_{1} = \frac{7}{5} R I

, ezt osztva

I

áramerősséggel kapjuk a négyszög eredő ellenállását,

\frac{7}{5} R

-t. Ezzel sorba van kapcsolva

R

ellenállás, így az áramkör teljes ellenállása

\frac{7}{5} R + R = \frac{12}{5} R

és az áramerősség:

I = U : \frac{12}{5} R = \frac{5 U}{12 R}

.

Az áramerősségek aránya:

\frac{I}{I_{0}} = \frac{5}{6}

3. U alakú csőbe, amelynek végei csappal elzárhatók, higanyt töltünk. A betöltött higanyszál teljes hossza

l

. A cső függőleges állásánál a cső mindkét szárában a higanyszint fölött

h

hosszúságú levegőoszlop van. Ha a csövet kissé megdöntjük, majd hirtelen visszaállítjuk függőleges helyzetébe, a higanyszál lengő mozgásba jön. A higanyszálat előbb a csapok nyitott, majd zárt állása mellett hozzuk lengésbe. Mennyi a két lengésidő hányadosa? A súrlódást ne vegyük figyelembe és tekintsünk el a levegő térfogatváltozása közben fellépő hőmérséklet-változásoktól is. A lengés amplitúdója igen kicsiny legyen

h

-hoz képest. Legyen

h

éppen egyenlő a barométerállással.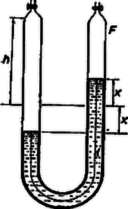

3. ábra

Megoldás: Azonnal a zárt csapok melletti esetet vizsgáljuk meg (3. ábra). A keresztmetszet területe

F

, a folyadék sűrűsége

d

, térfogata

F l

, tömege

F l d

x

darabbal történő elmozdulás esetében

2 x F d g

súlyú folyadékoszlop hidrosztatikai ereje viszi vissza a folyadékot eredeti helyzete felé.
Kezdetben mindegyik csőben a légnyomás

p_{0}

, a levegő nyomóereje

p_{0} F

és a levegő térfogata

h F

. Ha a folyadék

x

darabbal mozdult el, akkor a jobboldali csőben a levegő térfogata

(h - x) F

, és nyomása Boyle‐Mariotte törvénye szerint

p_{0} \cdot \frac{h}{h - x}

, az erő pedig

p_{0} F \cdot \frac{h}{h - x}

. Hasonlóan a baloldali csőben

(h + x) F

térfogatú,

p_{0} \cdot \frac{h}{h + x}

nyomású levegő

p_{0} F \cdot \frac{h}{h + x}

nagyságú nyomóerőt fejt ki a folyadék felszínére. A két levegőmennyiség eredőként a folyadékra

\begin{matrix} p_{0} F \cdot [\frac{h}{h - x} - \frac{h}{h + x}] = 2 p_{0} F h \cdot \frac{x}{h^{2} - x^{2}} \end{matrix}

nagyságú erőt fejt ki. A feladat szövege szerint csak kis kimozdulásokkal kell foglalkoznunk, ezért

x^{2}

-et elhanyagoljuk

h^{2}

mellett, így a levegők által kifejtett erők eredője:

\begin{matrix} \frac{2 p_{0} F x}{h}; \end{matrix}

hozzávéve a folyadékoszlop hidrosztatikai erejét, a folyadékot visszavivő teljes erő:

\begin{matrix} 2 x F d g + \frac{2 p_{0} F x}{h} . \end{matrix}

Látjuk, hogy a folyadékot a nyugalmi helyzetbe visszavivő erő egyenesen arányos

x

elmozdulással. Ebből következik, hogy rezgő mozgás keletkezik, amelyre érvényes az

m ω^{2} x

erőtörvény (

m

tömeg,

ω = 2 π / T

szögsebesség):

\begin{matrix} F l d ω^{2} x = 2 x F d g + \frac{2 p_{0} F x}{h} . \end{matrix}

Innen a lengésidő:

\begin{matrix} T = 2 π \sqrt[]{\frac{l}{2 g (1 + \frac{p_{0}}{d h g})}} . \end{matrix}

Ha a csapok nyitva vannak, akkor

h = \infty

, és ebben az esetben a lengésidő

\begin{matrix} T_{0} = 2 π \sqrt[]{\frac{l}{2 g}} . \end{matrix}

A lengésidők hányadosa:

\begin{matrix} \frac{T_{0}}{T} = \sqrt[]{1 + \frac{p_{0}}{d h g}} . \end{matrix}

d = 13, 6 {g/cm}^{3}

h = 76 cm

g = 981 {cm/sec}^{2}

p_{0} = 1 atm = 1013000 {din/cm}^{2}

, akkor a második tag is 1, és

T_{0} / T = \sqrt[]{2}

.
Néhány megjegyzés. A cső keresztmetszet területe mindenképp kiesik a számításból. Nyitott csapok esetében a folyadék sűrűsége sem számít, és a lengésidő annyi, mint egy

l / 2

hosszúságú fonálingáé. Zárt csapok esetében csak kis amplitúdók esetében tekinthető közelítően sinusnak a lengés. A valóságban a levegő térfogatváltozásai adiabatikusak, és kappa, a két fajhő hányadosa is odakerül a

p_{0} / d h g

tört mellé.

A II. forduló feladatai:

1. Ha

1 kg 0^{\circ}

-os víz megfagy (

0^{\circ}

-os jéggé alakul), akkor

80 kcal

hő szabadul fel. Mennyi hő szabadul fel

1 kg - 10^{\circ}

-os túlhűtött víz

10^{\circ}

-os állandó hőmérsékleten történő megfagyása közben? (Használjuk fel az energiamegmaradás tételét! A

0^{\circ}

és

- 10^{\circ}

között a jég és a víz sűrűségváltozását gyakorlatilag elhanyagoljuk).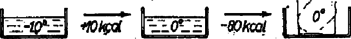

4. ábra

Megoldás: Két folyamatot hasonlítunk össze, amelyek kezdő és végső állapota azonos. Először a

- 10^{\circ}

-os vizet felmelegítjük

0^{\circ}

-os vízzé, amihez 10 kcal hőt kell beadnunk, azután a

0^{\circ}

-os vizet

0^{\circ}

-on megfagyasztjuk, amikor is 80 kcal hő leadása megy végbe (4. ábra).

5. ábra

Másodszor a

- 10^{\circ}

-os vizet ezen a

- 10^{\circ}

-os hőmérsékleten fagyasztjuk meg, amikor is

x

kcal hőt kell elvonnunk. A

- 10^{\circ}

-os jeget 5 kcal hőmennyiség beadásával melegítjük fel

0^{\circ}

-ra, mert a jég fajhője

0, 5

kcal/kg fok. (5. ábra)
Mindkét esetben a külső erők ellen végzett munka ugyanakkora, mert a feladat szövege szerint a víz és jég sűrűségkülönbsége mindkét hőmérsékleten ugyanakkorának veendő. Mindkét út esetében az 1 kg

H_{2} O

kezdeti és végső állapota azonos. Ebből következik, hogy a felvett hőmennyiségek, az energiamegmaradás törvénye szerint mindkét út esetében egyenlők:

\begin{matrix} 10 - 80 = - x + 5, \end{matrix}

innen a

- 10^{\circ}

-os túlhűtött víz olvadási hője:

\begin{matrix} x = 75 kcal/kg . \end{matrix}

2. Egy távcsőbe végtelenre akkomodált szemmel belenézve élesen látnánk a Nap képét. Mennyivel kell elmozdítanunk a távcső szemlencséjét, hogy az eredetileg tőle

16 cm

-re felállított ernyőn élesen jelenjen meg a Nap képe? A szemlencse fókusztávolságának abszolút értéke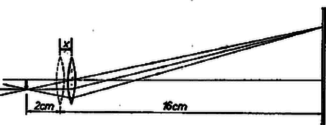

2 cm

6. ábra

Megoldás: A csillagászati távcső használatakor a tárgylencse és a szemlencse fókuszpontjai egybeesnek. A nagyon távoli tárgy képe a tárgylencse gyújtósíkjában keletkezik, és ez a kép a szemlencse számára tárgyként szerepel. A szemlencsét

x

darabkával kifelé húzva, az ernyőn reális kép keletkezik (6. ábra). A tárgytávolság

2 + x

, a képtávolság

16 - x

, ezért a lencsetörvény szerint: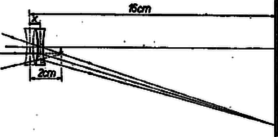

\begin{matrix} \frac{1}{2 + x} + \frac{1}{16 - x} = \frac{1}{2} . \end{matrix}

Rendezve:

\begin{matrix} x^{2} - 14 x + 4 = 0. \end{matrix}

Megoldása:

x = 7 \pm 3 \sqrt[]{5}

. A

0, 28

cm a számunkra használható eredmény, mert

13, 72

cm-es lencseeltolásnál is keletkezne reális kép, de rendkívül kicsinyített.

7. ábra

A Nap képének kivetítése a Galilei-féle távcsőnél is lehetséges (7. ábra). Ekkor a szemlencse szórólencse, amelyet a tárgylencséből érkező sugárnyalábba helyezünk, mielőtt a sugarak egyesülhettek volna. A szemlencsét ismét kifelé húzzuk

x

darabbal. Ekkor a tárgylencsétől érkező sugárnyaláb

2 - x

távolságban levő virtuális tárgyat jelent a szemlencse számára. A képtávolság

16 - x

. A lencsetörvény szerint:

\begin{matrix} \frac{1}{- (2 - x)} + \frac{1}{16 - x} = \frac{1}{- 2} . \end{matrix}

A tárgytávolság azért negatív, mert virtuális tárgyról van szó. A gyújtótávolság negatív, mert a szemlencse szórólencse. Rendezve:

\begin{matrix} x^{2} - 18 x + 4 = 0. \end{matrix}

Megoldása:

x - 9 \pm \sqrt[]{77}

. Az egyik megoldás (

17, 77

cm) a szemlencsének az ernyő mögé való helyezését kívánná. A másik megoldás (

0, 22

cm) adja a használható eredményt.

M

tömegű,

2 l

hosszúságú hasáb közepén

m

tömegű golyó nyugszik. A nulla időponttól kezdve

t

ideig a hasábra állandó

P

húzóerő hat. Ekkor az erőhatás megszűnik. Az alaplap és a hasáb közötti súrlódás elhanyagolható. A golyó és a hasáb közötti csúszó súrlódás biztosítja, hogy a golyó meg ne csússzék, hanem gördüljön. Mekkora

T

idő múlva esik le a golyó a hasábról? (Mikor éri el a golyó a hasáb szélét?) A golyó gördülő ellenállása elhanyagolható.

Megoldás: A golyó tömege

m

, rádiusza

r

, tehetetlenségi nyomatéka

I

, forgatásának szöggyorsulása

β

, középpontjának gyorsulása a vízszintes irányban végbemenő haladó mozgásánál

a

; a hasáb tömege

M

, gyorsulása

A

; az adott állandó erő

P

.
Vizsgáljuk a mozgás alakulását, ha a golyó és a hasáb közötti csúszó súrlódási együttható, nullától mindig nagyobb értékek felé növekszik. Ha

μ = 0

, akkor a hasáb nem képes a golyónak erőt átadni és a golyó mozdulatlanul marad (

a = 0

), miközben a hasáb

A = P : M

gyorsulással szalad el alatta.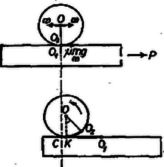

8. ábra

Most növeljük a súrlódási együtthatót egy bizonyos, kis

μ

értékre (8. ábra). Ekkor a golyó és a hasáb

O_{1} - O_{2}

érintkezési pontján

μ m g

súrlódási erő ébred, amely megmozgatja a golyót. A súrlódás révén a golyóra ható erő nem hat a golyó súlypontjában. Felveszünk két egyenlő nagy, ellentétes irányú,

μ m g

nagyságú erőt a golyó középpontjában (2 és 3). Ez megengedhető, mert a hozzáadott két erő eredője nulla. Most átcsoportosítjuk ezeket az erőket: a golyó középpontjában ható

μ m g

erő az

m

tömegű golyónak vízszintes irányban

a = μ g

gyorsulást ad (3), az 1. és 2. erők erőpárt alkotnak, amelynek erőkarja

r

, forgatónyomatéka

μ m r g

. Ez az erőpár a golyót a forgómozgás alaptörvénye értelmében

β = μ m r g / I

szöggyorsulással forgatja. Az adott teljes

P

erőből a hasáb gyorsítására

P - μ m g

marad, tehát a hasáb gyorsulása

\begin{matrix} A = \frac{P - μ m g}{M} . \end{matrix}

(1)

Tehát a hasáb

A

, a golyó középpontja

a

gyorsulással mozog jobb felé. Ez azt jelenti, hogy a golyó középpontjához képest a hasáb

A - a

gyorsulással távozik. Ugyanakkor a golyó kerületi pontjai

β r = μ m g r^{2} / I

gyorsulással mozognak. Amikor

μ

súrlódási együttható kicsiny, akkor a kerületi pontok

β r

gyorsulása kisebb, mint a golyó és a hasáb közötti

A - a

viszonylagos gyorsulás, ezért a golyó nem gördül simán a hasábon, hanem forgásában elmarad, csúszik. A 8. ábra alsó részén látható, hogy a hasáb közepén levő

O_{1}

pont

C

-ből

O_{1}

-be jutott. Ugyanakkor a golyó középpontja

C K

darabbal jutott előbbre, de a

μ m g

súrlódási erőből eredő forgatónyomaték csak

K O O_{2} ∢

-gel volt képes elforgatni, amitől az

O_{2}

kerületi pont a

K O_{2}

ívet írta le.

K O_{2}

ív rövidebb, mint a hasáb és golyó

K O_{1}

viszonylagos helyzetváltozása, így csúszás van, a hasáb elcsúszik a golyó alatt. A csúszás mértéke

A - a

viszonylagos gyorsulás és

β r

kerületi gyorsulás különbsége:

\begin{matrix} A - a - β r . \end{matrix}

(2)

9. ábra

10. ábra

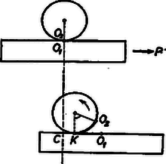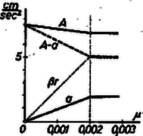Növeljük fokozatosan a súrlódási együtthatót. A golyó középpontjának

a

gyorsulása

a = μ g

függvény szerint lineárisan növekszik. A hasáb

A

gyorsulása (1) szerint lineárisan csökken. A 10. ábrán láthatók ezek az összefüggések. Magától értetődő, hogy

A - a

viszonylagos gyorsulás (szaggatott vonal) ugyancsak csökken. Viszont nagyobb súrlódási együttható mellett növekszik a golyó forgásának szöggyorsulása és a kerületi pontok

β r

gyorsulása (pontozott vonal). Növelve a súrlódási együtthatót, feltétlenül eljutunk ahhoz az esethez, hogy egyenlővé válik a viszonylagos gyorsulás a kerületi pontok gyorsulásával. Ez azt jelenti, hogy már nincs csúszás, helyébe lép a golyó sima legördülése (a 9. ábrán látható;

K O_{2} = K O_{1}

.). Az ehhez szükséges súrlódási együtthatót megkapjuk, ha a (2)-vel kifejezett csúszás mértékét nullával tesszük egyenlővé:

\begin{matrix} A - a - β r = 0. \end{matrix}

Ide helyettesítjük

β r

helyébe

μ g m r^{2} / I

-t,

a

helyébe

μ g

-t és

A

helyébe az (1) alatti eredményt:

\begin{matrix} \frac{P - μ g (m + M)}{M} - \frac{μ g m r^{2}}{I} = 0. \end{matrix}

Innen a súrlódási együtthatónak az a kritikus értéke, amely elegendő a sima legördüléshez:

\begin{matrix} μ_{k} = \frac{P}{M g (1 + \frac{m}{M} + \frac{m r^{2}}{I})} . \end{matrix}

Ezzel kifejezve a sima legördülés esetében a golyó középpontjának gyorsulása:

\begin{matrix} a = \frac{P}{M (1 + \frac{m}{M} + \frac{m r^{2}}{I})} . \end{matrix}

(3)

a hasáb gyorsulása:

\begin{matrix} A = \frac{P (1 + \frac{m r^{2}}{I})}{M (1 + \frac{m}{M} + \frac{m r^{2}}{I})}, \end{matrix}

(4)

a viszonylagos gyorsulás, illetve a kerületi pontok gyorsulása:

\begin{matrix} A - a = β r = \frac{P \cdot \frac{m r^{2}}{I}}{M (1 + \frac{m}{M} + \frac{m r^{2}}{I})} . \end{matrix}

(5)

Ha a súrlódási együttható tovább növekszik a kritikus értéknél, minden ugyanúgy marad. Igaz, hogy

μ m g

algebrai kifejezés értéke mindig nagyobb lesz, de ez a szorzat azt a lehetséges legnagyabb súrlódási erőt jelenti, amely létrejöhet, de nem biztos, hogy létrejön. A kísérletben tényleg fellépő

a

gyorsulást nagyobb

μ

mellett is (3) adja meg. Ennél nagyobb golyónak átadott erő olyan nagy gyorsulású forgást jelentene, hogy a golyó sima legördülés helyett a hasábon előrecsúszna. Ez azonban lehetetlen, mert a súrlódási erő olyan erő, amely akadályozza a mozgást, de nem képes előregurítani egy golyót. Nem szabad elfelejtenünk, a (

μ \cdot erő

) képlet azt a lehetséges legnagyobb súrlódási erőt adja meg, amely adott esetben keletkezhet, de egyáltalán nem jelenti azt, hogy mindig ekkora súrlódási erőnek kell fellépnie. A padlón álló láda esetében a működő súrlódási erő nulla. Ha túllépjük a

μ_{k}

súrlódási együtthatót, minden marad ugyanúgy. A feladat tulajdonképpeni megoldását a (3), (4) és (5) képletek jelentik, mert a feladatban akkora súrlódási erőt követeltek meg, hogy sima legördülés legyen.

A feladat tanulmányozására alkalmas numerikus feladat adatai lehetnek például:

m = 100 gramm

r = 2 cm

I = 160 {gcm}^{2}

M = 400 gramm

P = 3000 din

. Erre vonatkoznak a 10. ábra grafikonjai. A 8. ábra

μ = 0, 001

, a 9. ábra

μ_{k} = 0, 002

súrlódási együttható mellett mutatja a golyó és hasáb helyzetét induláskor és 1 sec múlva.
A feladat többi kérdését is ezekhez az adatokhoz kapcsolódva vizsgáljuk meg. Legyen a hasáb fél hosszúsága

l = 40 cm

. A golyó középpontja

A - a = 5 {cm/sec}^{2}

viszonylagos gyorsulással szalad a hasábon. A 40 cm-es táv megtételére

\begin{matrix} t_{0} = \sqrt[]{\frac{2 l}{A - a}} = 4 sec \end{matrix}

időre van szüksége. Ha az erő működésének ideje ennél több, például

t = 6 sec

, akkor a golyó leeséséhez szükséges időt

t_{0}

adja meg. Ha az erő működésének ideje

t_{0}

-nál kevesebb, például

t = 2 sec

, akkor a golyó ezalatt gyorsulva megtesz

\frac{A - a}{2} \cdot t^{2} = 10 cm

utat, és így marad még

l - \frac{A - a}{2} \cdot t^{2} = 40 - 10 = 30 cm

. Ezt az utat a golyó

(A - a) t = 10 cm/sec

sebességgel egyenletesen futja be, tehát az egyenletes mozgás ideje

τ = [l - \frac{A - a}{2} \cdot t^{2}] : (A - a) t = 3 sec

. A láda végének eléréséhez szükséges teljes idő

t + τ = 5 sec