Kezdőlap


Cím:	Hullámok interferenciája. Koherencia
Szerző(k):	Bodó Zalán
Füzet:	1963/március, 161 - 170. oldal	PDF \| MathML
Témakör(ök):	Szakmai cikkek

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Hullámjelenségek interferenciájának vizsgálatát kezdjük talán a legegyszerűbb hullámjelenség, a húron kialakuló transzverzális mechanikai hullámok tanulmányozásával. Vizsgáljuk meg egy igen hosszú (vizsgálataink szempontjából végtelen hosszúnak tekinthető), koordináta-rendszerünk $x$ tengelyében kifeszített (befogási helyei az $x = 0$ ponttól igen távol vannak) húron kialakuló hullámmozgást, ha a húrnak $x = 0$ pontját a $t = 0$ időpillanattól kezdve valamilyen külső erővel $T$ rezgésidejű csillapítatlan harmonikus rezgőmozgásra kényszerítjük. Ilyenkor azt tapasztaljuk, hogy a húron az $x = 0$ pontból jobbra és balra haladó hullámok alakulnak ki. A húr alakja az idő folyamán az 1. ábrán látható módon változik. Itt $y$ a húr pontjainak kitérése az egyensúlyi helyzethez képest, $A$ a maximális kitérés, az amplitúdó, $λ$ a hullámhossz.

1. ábra

E jelenség térbeli és időbeli lefolyását matematikailag tehát a következőképpen írhatjuk le. A hullámok haladási sebességének abszolút értéke:

c = \frac{λ}{T}

lesz. 0-tól

t

ideig tehát a hullámok jobb oldalon az

x = c t

, baloldalon az

x = - c t

távolságig hatolnak el. Jobb oldalon a

0 ≦ x ≦ c t

szakaszon a kitérést az

\begin{matrix} y = A sin (\frac{2 π}{T} t - \frac{2 π}{λ} x) \end{matrix}

(1)

egyenlettel, a

- c t ≦ x ≦ 0

szakaszon pedig az

\begin{matrix} y = A sin (\frac{2 π}{T} t + \frac{2 π}{λ} x) \end{matrix}

(2)

egyenlettel írhatjuk le. Az előbbi az

x

tengely mentén

c

, az utóbbi az

x

tengely mentén

- c

sebességű haladó hullám egyenlete.
Vizsgáljuk meg, hogy mit jelent pl. az (1) egyenlet. Ez egyrészt megadja a húr valamely (a fenti korlátozásoknak megfelelő) tetszőleges pontjának időbeli mozgását. A húrnak valamely

x = x_{0}

kiválasztott pontja, ha már a hullám ezt a pontot elérte

(t > \frac{x_{0}}{c})

, csillapítatlan rezgőmozgást végez az

\begin{matrix} y = A sin [\frac{2 π}{T} t - (\frac{2 π x_{0}}{λ})] \end{matrix}

(3)

egyenletnek megfelelően. Az összes rezgő pontok amplitúdója

(A)

ugyanakkora, a

- \frac{2 π x_{0}}{λ}

kezdőfázis pontról pontra változik. L. 2. ábra. A hullámmozgás kialakulása után a húr egy pontjában a mozgás időbeli képe tökéletes hasonlóságot mutat egy időpontban a mozgás térbeli képéhez (a húr alakjához). Az egymásnak megfelelő mennyiségek:

\begin{matrix} Időben: & T,   térben:λ, \\ Időben: & a\frac{2 π}{T} = ωkörfrekvencia, \\ térben: & a\frac{2 π}{λ} = khullámszám. \end{matrix}

Az utóbbi fogalmak bevezetésével az (1) egyenlet az egyszerűbb

\begin{matrix} y = A sin (ω t - k x) \end{matrix}

(4)

alakra hozható.

2. ábra

A 2. ábrából megállapíthatjuk, hogy a húrnak már mozgó pontjai csillapítatlan harmonikus rezgőmozgást végeznek, és ennek megfelelően energiára tettek szert. Ez az energia kinetikus és potenciális energiából tevődik össze, melyek az időben periodikusan változnak. Mivel a húr végtelen kicsi hosszúságának végtelen kicsi a tömege is, ez az energia a már rezgő szakaszon folytonosan oszlik el. Ezért a húr mentén energiasűrűségről beszélhetünk, mely a már mozgásba jött helyeken időben közepesen állandó, és így az energia közepes sűrűsége, e számértékre nézve egyenlő az egységnyi hosszúságra eső időbeli közepes energiával (dimenziója: energia/hosszúság). A 0 időpillanatban a húr energiája még 0 volt. A későbbi

t

időpillanatban viszont, mivel a húrból

2 c t

hossz már rezeg, a húr energiája:

E = 2 e c t

. A húron haladó hullám létrehozásához tehát energia szükséges, kívülről egységnyi idő alatt az

x = 0

pontban

2 e c

energia mennyiséget kell betáplálnunk. Ez az energia e pontból kiáramlik (vagy úgy is szokás mondani: kisugárzódik),

e c

energia áramlik jobbra és ugyanekkora balra is.

c

tehát nemcsak a hullám terjedési sebessége, hanem az

e

sűrűségű energia áramlási sebessége is. Energetikai szempontból tehát pl. a jobbra haladó hullámnál arról van szó, hogy a húr pontjai úgy végzik csillapítatlan rezgőmozgásukat, hogy a jobb oldali szomszédos pontok által okozott csillapítás (energia fogyasztás) pontosan ugyanakkora, mint a bal oldali szomszédos pontok által történő gerjesztés (energia betáplálás).
A húrnál megismert ezen legegyszerűbb hullámjelenség a természetben előforduló más hullámjelenségek lényeges tulajdonságait is visszatükrözi. Valamilyen rezgőmozgást végző test, elektromos rezgőkör stb. többnyire hullámokat kelt, hullámokat bocsát ki magából. Ezek mechanikai hullámoknál a környező közeg, elektromágneses hulámoknál az elektromágneses tér hullámai, melyek energiaáramlást jelentenek. A hullámkibocsátás így energia fogyasztást igényel, és ezért végeredményben az eredeti rezgés csillapítását jelenti. A hullámban

c

sebességgel haladó energiasűrűség a húrnál állandó volt, síkbeli hullámoknál (pl. folyadékok felületi hullámai) a kisugárzott energia mind nagyobb és nagyobb kör kerületén, térbeli hullámoknál pedig mind nagyobb és nagyobb gömbfelületen oszlik el, ezért a hullámforrástól távolodva az energiasűrűség csökken. Ennek megfelelően az amplitúdó is csökkenést mutat.

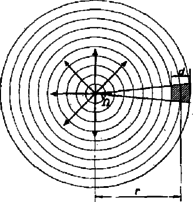3. ábra

Ha azonban a hullámforrástól nagy távolságra, kis tartományban (

Ω

kicsi,

d ≪ r

) lejátszódó jelenségeket vizsgálunk, jó közelítéssel az amplitudó változását elhanyagolhatjuk (a 3. ábrán a vonalkázott tartományban a gömbfelületeket síkokkal helyettesíthetjük) a gömbhullámokat közelítőleg síkhullámokkal írhatjuk le. Ilyen közelítésben most a hullámegyenlet a következő alakban irható:

\begin{matrix} y = A sin (\frac{2 π}{T} t - \frac{2 π}{λ} r) \end{matrix}

(5)

ahol

r > 0

a hullámforrástól való távolságot jelzi. Ez az általánosabb kifejezés magába foglalja nemcsak az (1), hanem pl. a (2) egyenletet is. Itt ugyanis az

x

tengely negatív oldalán a hullámforrás távolsága

- x

lévén:

\begin{matrix} y = A sin [\frac{2 π}{T} t - \frac{2 π}{λ} (- x)] \end{matrix}

(2a)

Ezek után térjünk vissza a húrhoz. Legyen megint egy hullámforrásunk, mely az

x = 0

helyen a

t = 0

időpillanattól kezdve sugároz, és vizsgáljuk a jobbra terjedő hullámokat. Legyen ezenkívül az

x = D

pontban egy másik ugyanolyan frekvenciájú és az egyszerűség kedvéért ugyanolyan amplitúdójú hullámforrásunk, amelyik azonban egy tetszőleges, de későbbi

t_{0} > 0

időpillanatban kezd csak sugározni. Ennél viszont a balra terjedő hullámokat vizsgáljuk. A viszonyokat a 4. ábrán tüntettük fel. Vizsgáljuk meg a húr kitérésének alakulását az

L

szakaszon, ahová már mind a két hullám elérkezett. Vizsgálatunkat korlátozzuk az ábrán feltüntetett esetre, mikor még az egyes hullámforrások hullámai nem érték el a másik hullámforrást. (Ezáltal az ott jelentkező reflexiókkal, melyek erősen bonyolítanák a jelenséget, nem kell számolnunk.) Tapasztalat szerint ilyenkor a két hullám találkozásánál az eredő kitérés egyszerűen a két eredeti kitérés összegeként kapható meg. Ezt a jelenséget nevezzük interferenciának. Milyen alakot kapunk tehát a húrra, ha ezt az előbbieknek megfelelően matematikailag pontosan kiszámítjuk?

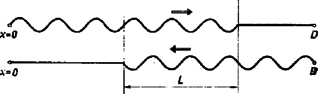4. ábra

A jobbra haladó hullámot az

\begin{matrix} y_{1} = A sin (\frac{2 π}{T} t - \frac{2 π}{λ} x) \end{matrix}

(6)

egyenlet írja le. A balra haladó hullámot leíró egyenletnél tekintetbe kell vennünk, hogy egyrészt az csak a

t - t_{0}

időpillanattól kezd sugározni, másrészt, hogy az

x

pontnak a hullámforrástól való távolsága most

D - x

. Ezért az

\begin{matrix} y_{2} = A sin [\frac{2 π}{T} (t - t_{0}) - \frac{2 π}{λ} (D - x)] \end{matrix}

(7)

egyenlet írja le a balfelé haladó hullámot. A két hullám eredője tehát

\begin{matrix} y = y_{1} + y_{2} \end{matrix}

(8)

lesz. Tekintetbe véve a közismert

\begin{matrix} sin α + sin β = 2 cos \frac{α - β}{2} sin \frac{α + β}{2} \end{matrix}

(9)

összefüggést:

\begin{matrix} y = 2 A cos (\frac{2 π}{λ} x - \frac{π t_{0}}{T} - \frac{π D}{λ}) sin (\frac{2 π}{T} t - \frac{π t_{0}}{T} - \frac{π D}{λ}) . \end{matrix}

(10)

A húr pontjai itt mind azonos

- \frac{π t_{0}}{T} - \frac{π D}{λ}

kezdő fázisú harmonikus rezgőmozgást végeznek, azonban az amplitúdó pontról pontra változik, értéke:

2 A cos (\frac{2 π}{λ} x - \frac{π t_{0}}{T} - \frac{π D}{λ})

. Az

L

szakaszon tehát állóhullámok alakulnak ki. A húr alakjának időbeli változását az 5. ábrán láthatjuk.

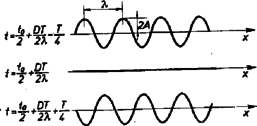5. ábra

A húron egyes pontok kétszer akkora amplitúdóval rezegnek, mint az egyes haladó hullámoknál (maximális erősítés), egyes pontok pedig állandó nyugalomban maradnak (teljes kioltás). Maximális erősítésűek azok a helyek, ahol a

cos

függvény argumentuma

\frac{π}{2}

párosszámú többszöröse, teljes kioltás van, ahol az argumentum

\frac{π}{2}

páratlan számú többszöröse. Az előbbi helyeken tehát:

\begin{matrix} \frac{2 π}{λ} x - \frac{π t_{0}}{T} - \frac{π D}{λ} = 2 n \frac{π}{2}, \end{matrix}

(11)

az utóbbiakon pedig

\begin{matrix} \frac{2 π}{λ} x - \frac{π t_{0}}{T} - \frac{π D}{λ} = (2 n + 1) \frac{π}{2} . \end{matrix}

(12)

Megfelelő egyszerűsítés és átrendezés után:

\begin{matrix} x - (D - x) - \frac{t_{0} λ}{T} = 2 n \frac{λ}{2}, \end{matrix}

(11a)

illetve

\begin{matrix} x - (D - x) - \frac{t_{0} λ}{T} = (2 n + 1) \frac{λ}{2} . \end{matrix}

(12a)

Ezen egyenletek baloldalán három tag szerepel, a hullámforrásoktól való távolságok különbsége, vagy ahogy röviden mondani szoktuk, a hullámok ,,útkülönbsége'' és a hullámforrások időbeli fáziskülönbségéből származó

\begin{matrix} \frac{t_{0} λ}{T} = t_{0} c út. \end{matrix}

Ha ezen utóbbi tag az időben állandó, a két hullámforrást koherens hullámforrásnak nevezzük. Ilyenkor pl. a (12a) egyenletekkel megállapított

x

helyeken csomópont, állandóan nyugalom, 0 kitérés lesz, az interferencia jelensége jól megfigyelhető. Mikor lesz

t_{0} c

időben állandó, és mi okozza ennek időbeli változását? A hullámforrást ‐ miként láttuk ‐ a hullámkibocsátás csillapítja. Ha a hullámforrás olyan, hogy a kisugárzott energiát folytonosan tudjuk pótolni,

t_{0} c

állandóan tartható. Folyadékok felületi hullámainál pl. a 6. ábrán bemutatott elrendezésnél a folyadék felületét hullámmozgásba hozó

A

és

B

testek az

l

merev rúddal mechanikailag össze vannak kötve, a kar rezgésekor a két hullámforrás koherenciája ezáltal biztosítva van. (Most

t_{0} = 0

lévén, pl. teljes kioltáshoz elegendő, ha az útkülönbség egyszerűen a félhullámhossz páratlan számú többszöröse). Vagy pl. a két egyforma rádióantennát ugyanarról a berendezésről vezérelve, az előbbi esethez hasonlóan koherens elektromágneses hullámzást hozhatunk létre.

6. ábra

Nehezebb a helyzet akkor, ha a sugárzó hullámforrások energiája nem pótlódik folyamatosan, hanem az energiautánpótlás lökésszerű. Ilyenkor, ha ezen energialökések a két hullámforrásban egymástól függetlenül rendszertelenül következnek be, a hullámok csak két ilyen lökés közötti középértékben ,,

t_{k}

'' időszakaszokon belül koherensek, mert minden egyes energiautánpótlás nagy erősségű új hullámzás megindulásának felel meg (a már lecsillapodott vagy erősen lecsillapodásban levő előbbi sugárzáshoz képest), és így az energiautánpótlás időben rendszertelen volta miatt a

t_{0} c

tag értéke közepesen ,,

t_{k}

'' időszakonként megváltozik. Interferencia bár most is van, de a (12a) egyenletben az utolsó tagnak megváltozása miatt a teljes kioltást mutató helyek az időben állandóan változnak, és így az interferencia észlelhetőségének feltételévé válik, hogy az észleléshez szükséges idő

t_{k}

-nál jóval kisebb legyen. Pl. két lassan csillapodó, hosszú ideig csengő hangvilla közötti interferencia észlelhető, ugyanezt két hegedűvel már észlelni nem lehet. Hegedű esetében ugyanis gyorsan csillapodó és a vonó által igen rövid időközökben újra és újra gerjesztett rezgések keletkeznek (a vonó húzásakor a húr hozzá-hozzá tapad a vonóhoz és el-el szabadul tőle).
Ilyen esetekben is lehet azonban észlelhető interferenciát létrehozni úgy, hogy az egyazon hullámforrásból kiinduló hullámokat önmagukkal hozzunk interferenciába. Ennek a legegyszerűbb módja, hogy visszaverődés vagy törés segítségével másik hullámforrásként az eredeti hullámforrás képét vagy képeit használjuk föl.

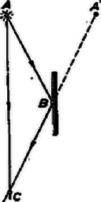7. ábra

Pl. a 7. ábrán az

\bar{A C}

szakaszon közvetlenül haladó és az

\bar{A B} + \bar{B C}

tört úton haladó hullámok interferenciaképesek lesznek az utóbb említett lökésszerű energiautánpótlás esetén is, ha az

\frac{\bar{A B} + \bar{B C}}{c} - \frac{\bar{A C}}{c}

idő kicsi

t_{k}

-hoz képest. Ilyenkor tehát jó közelítéssel (az idő legnagyobb részében)

t_{0} = 0

. Ilyen esetekben éppen abból a körülményből, hogy mekkora útkülönbségekig jelentkezik interferencia az esetleg ismeretlen

t_{k}

értékére következtethetünk. Pl. a 8. ábrán látható módon két tükörkép segítségével az útkülönbség ‐ ha szükséges ‐ a 7. ábrabelinél is kisebbé tehető.

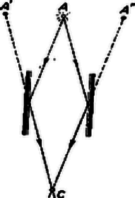8. ábra

Ma már tudjuk, hogy a fény az elektromágneses sugárzás egyik fajtája. Hosszú időbe telt azonban, amíg a fény interferencia-képességét, és így a fény hullámtermészetét kísérletileg sikerült igazolni, és a fényinterferencia kísérletek ma is körültekintő gondosságot igényelnek. Ennek egyik oka fényhullámok igen kicsiny hullámhossza, másik ok azonban éppen az, hogy a koherencia feltételei nem éppen egyszerűen teljesíthetők.
A fényforrások interferenciájára vonatkozó tapasztalatok a következő három pontban foglalhatók össze:
1. Két különböző fényforrással sohasem sikerül kimutatható interferenciát létrehozni.
2. Ha egyetlen fényforrás segítségével hozunk létre interferenciát, az csak kb. pár dm útkülönbségig lehetséges (ez az úthossz függ a fényforrás minőségétől!).
3. Általában egyetlen fényforrás esetében is két egymástól csak igen kis szögben különböző irányban kibocsátott fénysugárral lehet interferenciát kimutatni.
Az előzőek alapján az 1. és 2. pontokban leirt észleléseket már könnyen meg tudjuk magyarázni. Ha közepesen 3 dm útkülönbséget veszünk fel az interferencia-képesség határának, ennek

t_{k} = \frac{0, 3 m}{c} = \frac{0, 3 m}{3 \cdot 10^{8} m {sec}^{- 1}} = 10^{- 9} sec

felel meg. A fényt a fényforrás atomjai bocsátják ki. Tehát kb.

10^{- 9}

sec ideig tart egy elemi fénykibocsátó folyamat. (Természetesen ‐ mint már említettük ‐ a pontos érték erősen függ attól, hogy milyen atomról van szó.) Az interferenciakép két különböző fényforrásnál csak ennél lényegesen rövidebb ideig változatlan. Ilyen gyorsan változó fényjelenségeket természetesen szemünk nem tud észlelni.
Mivel két különböző fényforrás atomjai egymástól függetlenül közepesen

t_{k}

ideig sugároznak, interferencia csak ugyanazon atom által kisugárzott fénnyel hozható létre. Ennek megvalósítását a 7. ábrának megfelelő elgondolás szerint a 9. ábrán láthatjuk.

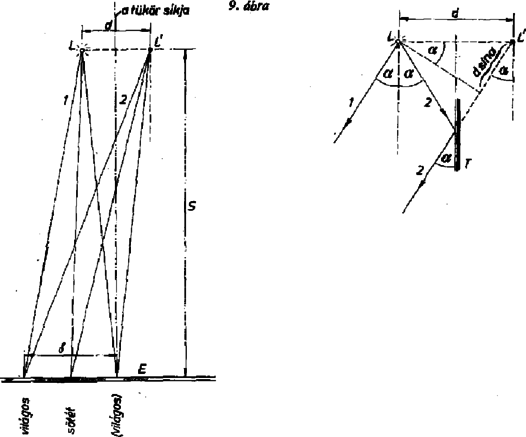9. ábra

L

világító pontnak lehetőleg közeli

d

távolságú

L'

képét állítottuk elő a

T

tükör segítségével.

L

és

L'

-től nagy

S

távolságra elhelyezett

E

ernyőn észleljük az interferencia jelenséget.

δ

legyen két szomszédos világos hely távolsága az ernyőn. Az ábrán bejelölt 1. és 2. sugarak interferenciája hozza létre az első maximális erősítést a tükör síkjától

δ

távolságra. Az interferenciát létrehozó 1. és 2. sugár egymással az

L

fénypontnál

2 α

szöget zár be. A 3. pont szerint ennek kell igen kicsinek lennie. (E feltétel a tükörnél igen nagy, közel

90^{\circ}

beesési szöget jelent, ami a kísérlet kivitelezésénél nagyon nehéz beállítási munkát jelent.) Mivel az

E

ernyő a későbbiekben látható okok miatt nagy távolságra van, a 2. fénysugár a tükrön való visszaverődés után jó közelítéssel az 1.-vel párhuzamosnak vehető. Így a tükör síkjától

δ

távolságra jelentkező első világos jelnél a két sugár útkülönbsége az ábra szerint

\begin{matrix} d sin α = λ \end{matrix}

(13)

kell legyen. Mivel

α

kicsi,

\begin{matrix} α ≃ sin α ≃ tg α = \frac{δ}{S} . \end{matrix}

(14)

\begin{matrix} λ = d \frac{δ}{S}, és δ = \frac{S}{d} λ \end{matrix}

(15) (16)

Tehát

d, δ

és

S

ismeretében

λ

a (15) egyenlet segítségével meghatározható. Közismerten a látható tartományban

λ

4 \cdot 10^{- 7}

m és

8 \cdot 10^{- 7}

m között változik, ha csak a nagyságrend érdekel, közepesen

5 \cdot 10^{- 7}

m-nek vehető. Ahhoz, hogy szemmel jól megkülönböztethető világos-sötét csíkokat kapjunk,

δ

-nak lehetőleg nagynak kell lennie. Ez

λ

ismeretében (16) alapján úgy érhető el, ha

α

lehetőleg kicsi, és

S

lehetőleg nagy. Ezzel körülbelül érzékelhetők a

λ

kicsinységéből eredő nehézségek. Ugyanezen a példán nagyon jól megérthető, hogy miért kell

α

-nak általában igen kicsinynek lennie. Egy-egy atom által keltett fényenergia olyan kicsi, hogy szemünkkel nem észlelhető. A jól észlelhetőséghez sok-sok világító atom együttes fénye szükséges. Általában minden atom a saját tükörképével interferencia csíkokat hoz létre. Ezek azonban sok-sok világító atom esetében általában mind különböző helyeken lesznek, és az interferencia nem észlelhető. Hétköznapi megfigyeléseink szerint tudjuk, hogy közönséges esetekben a lámpa és a tükörképe nem hoz létre interferenciát. Van azonban lehetőség arra, hogy sok-sok atom esetén is észlelhessünk interferenciát.

10. ábra

Nézzük meg a 10. ábrát. Itt a tükörre merőleges

l

hosszúságú kiterjedt fényforrás interferencia viszonyait tüntettük fel. A fényforrás egyik végpontjában világító

L

atom

L'

tükörképével az előzőek szerint abban az

α

irányban fog (először) teljes kioltást adni, melyre

\begin{matrix} d sin α = \frac{λ}{2} . \end{matrix}

(17)

A fényforrás másik végpontján világító

M

atomra ugyanez a feltétel:

\begin{matrix} (d + 2 l) sin α = \frac{λ}{2} . \end{matrix}

(18)

Nyilvánvaló, hogy (17) és (18) egymásnak ellentmond, csak

α

különböző értékeivel elégíthető ki. Ha azonban teljesül a

\begin{matrix} 2 l sin α ≪ λ \end{matrix}

(19)

feltétel, akkor jó közelítéssel kielégül ugyanazon

α

-ra (17) és (18) is. Vagyis ilyenkor az

L - L'

interferencia csíkjaival lényegében azonos helyzetűek lesznek

M - M'

interferencia csíkjai is, és ez a feltétel még inkább teljesül a fényforrás bármely közbenső világító atomjára.
A (19) koherenciafeltétel megszabja, hogy kiterjedt fényforrásoknál milyen

α

szögig interferenciaképesek a fénysugarak, mintegy megmondja, milyen szöghatárokon belül tekinthető a fényforrás interferencia szempontjából pontszerűnek. A fény hullámhosszának kicsinysége miatt e (19) feltétel teljesítése általában csak úgy lehetséges, ha egyrészt

l

-et minél kisebbre választjuk (keskeny rés segítségével e méretet lecsökkenthetjük), főleg pedig

α

-t igyekszünk igen kicsinyre beállítani.

11. ábra

Speciális esetekben

α

olyan kicsiny lehet, hogy az

l

méretre különösebb korlátozódás nem is adódik. Ez az eset fordul elő például igen vékony hártya két felületéről kiinduló reflektált sugarak interferenciájánál. Az itt bekövetkező viszonyokat a 11. ábra tünteti fel. Ezen a

d

vastagságú vékony hártyát torzítottan nagynak választottuk és a vékony hártyán a fénysugarak törését első közelítésben elhanyagoltuk. A vékony hártyától

r

távolságra levő

L

lámpából kiinduló, és a hártya első felületén reflektálódó fénysugarak az

L'

, a hátsó felületén reflektálódó sugarak az

L''

virtuális képektől kiindulónak látszanak, és a hártyától

s

távolságra elhelyezett

E

ernyőn interferenciát hoznak létre. Az útkülönbség a

γ

szög függvénye. Ezért az

E

ernyőn koncentrikus világos és sötét gyűrűk jelennek meg, annak megfelelően, hogy erősítés vagy kioltás áll-e elő. Az ábrából látható, hogy az interferenciát létrehozó sugarak által bezárt szög

2 α

(a két ívvel és egy ívvel jelölt szögek különbsége) igen kicsi, és így:

\begin{matrix} sin 2 α \approx 2 α \approx tg 2 α = \frac{2 d sin γ}{\frac{s + r}{cos γ}} = \frac{d sin 2 γ}{s + r} . \end{matrix}

(20)

Legyen pl. egy gyakorlatilag megvalósítható esetben

d = 10^{- 5} m

r = 3 dm

s = 7 dm

sin 2 γ = 0, 1

. Ilyen elrendezésben tehát

2 sin α \approx sin 2 α \approx 10^{- 6}

értékre csökkenthető. A fényforrás méreteinek (19) korlátozó feltétele most:

\begin{matrix} l \cdot 10^{- 6} ≪ 5 \cdot 10^{- 7} m, \end{matrix}

tehát

\begin{matrix} l ≪ 0, 5 m . \end{matrix}

Vagyis most a fényforrás kiterjedése elég nagy lehet. A

d

vastagság további csökkentésével,

s

és

r

növelésével, és lehetőleg merőleges beesésnél (

γ

csökkentése) a (19) feltétel gyakorlatilag nem jelent korlátozást. Ezért látunk interferencia-jelenséget vékony szappanbuborékon, vízre kiöntött olajrétegen vagy a közismert Newton-féle gyűrűs kísérletben, kiterjedt fényforrások alkalmazásakor is.

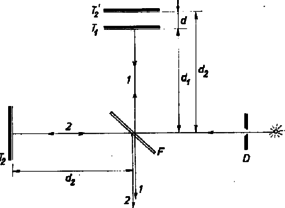12. ábra

Viszont ha fényforrásunknál továbbra is korlátozzuk az

l

méretet, továbbá

s

-et és

r

-et nagynak,

γ

-t pedig most is igen kicsinek választjuk,

d

méreteivel mehetünk feljebb, akár

m

nagyságrendig is. Ez valósul meg a 12. ábrán látható Michelson-féle interferométernél. Az

F

fényforrás fényét a

D

diafragmával korlátozzuk (l), a fénysugár ezután a

45^{\circ}

alatt elhelyezett

F

félig áteresztő tükörre esik. A fénysugár egyik része (1) visszaverődik, és a

T_{1}

tükörre jut. Ott ismét visszaverődik, és az

F

félig áteresztő tükrön egy része keresztül halad. A fénysugár másik része (2) keresztülhalad az

F

tükrön, a

T_{2}

tükrön reflektálódik, majd egy része az

F

tükrön újabb reflexiót szenved. A (2) fénysugár úgy fogható fel, mint ha a

T'_{2}

virtuális tükrön reflektálódott volna. Így az (1) és (2) sugarak általában távcsővel megfigyelt interferenciája tökéletes hasonlóságot mutat az előbbi esethez, most a két reflektáló felület távolsága

d = d_{2} - d_{1}

a tükrök távolságának különbsége. Pl. a

d_{2}

távolság változtatásával

d

értéke változtatható, kioltás ott lesz (l. 11. ábra^{$^{*}$}), ahol (

γ

értéke kicsi, amennyire csak lehetséges, merőleges beesést valósítunk meg)

\begin{matrix} 2 d cos γ \approx 2 d = (2 n + 1) \frac{λ}{2} . \end{matrix}

(21)

Ha a

d

távolság folyamatosan változik, az interferencia-gyűrűk folyamatosan befelé vagy kifelé elmozdulnak.

d = \frac{λ}{2}

út megtétele után a kioltás helyei ugyanott lesznek, mint a kiinduláskor, vagyis ha az interferencia-képnek ugyanazt a helyét vizsgáljuk, ezen elmozdulás alatt az eredeti sötét hely világossá vált, majd újra elsötétedett: az interferencia-gyűrű egyet lépett. Ily módon sikerült Michelsonnak a fényhullámhosszal az ősmétert összehasonlítania. Ez csak több lépésben (

d_{1}

és

d_{2}

váltakozó mozgatásával) volt lehetséges, mert miként már említettük, ha az útkülönbség pár dm-nyi hosszúságot elér, az interferenciaképesség megszűnik. (Többek között épp ennek a hossznak megállapítására is használható ez az interferométer.) Így ma már a métert, mint fizikai egységet, a 86-os tömegszámú kripton atom

2 p_{10}

és

5 d_{5}

energiaszintjei közötti átmenetnek (ily módon egy speciális jól előállítható szín van definiálva) megfelelő sugárzás vákuumban való hullámhosszúságának 1 650 763,73-szorosaként definiáljuk.
A (19) koherencia feltétellel kapcsolatban láttuk, hogy az interferenciakísérleteknél ‐ mindig igen kis

α

szögek fordulnak elő. A fénysugárzással foglalkozva Einstein azt a gondolatot vetette fel, hogy az atom tűsugarakat bocsát ki magából, csak egy irányba, pontosabban igen kis nyílású kúp térszögébe bocsát ki fényt. A magyar Selényi Pálnak sikerült ezt az elméletet kísérletileg megcáfolnia, és nagy

α

szögek mellett is interferenciát létrehoznia. Ő a (19) feltételt úgy elégítette ki, hogy fényforrásként lumineszkáló anyagot választott, melynél az

l

méretet annyira le tudta csökkenteni, hogy a (19) feltétel nagy szögekre is teljesült, és az interferenciát nagy szögeknél is észlelni lehetett. (Selényi Pál nagyszögű interferencia kísérlete 1911.)

Dr. Bodó Zalán

^{$^{*}$}A pontosság kedvéért meg kell jegyeznünk, hogy vékony hártyánál a feltétel nem ez, mert ott tekintetbe kell venni még azt a körülményt is, hogy az egyik reflexiónál a reflexió optikailag ritkább, a másik optikailag sűrűbb tömegen történik. A Michelson-féle interferométernél erről nincs szó, egyszerűen

d_{2} - d_{1}

útkülönbséggel számolhatunk.