Cím: Az 1963. évi Országos Középiskolai Matematikai Tanulmányi Verseny II. fordulóján kitűzött feladatok megoldása
Szerző(k):  Surányi János 
Füzet: 1963/november, 102. oldal  PDF  |  MathML 
Témakör(ök): OKTV

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

1. feladat. Oldjuk meg a következő egyenletet:

sinx+cosx+sinxcosx=1.(1)

 
I. megoldás. Világos, hogy nem lehet mindkét fellépő szögfüggvény negatív. Belátjuk, hogy egyik sem lehet az. Ha ugyanis pl. sinx<0, cosx≥0, akkor a bal oldalt
sinx+cosx(1+sinx)
alakban írva 0≤1+sinx<1, így mindkét tag abszolút értéke kisebb, mint 1, és az első tag negatív, tehát a kifejezés kisebb, mint 1. Hasonlóan látható, sinx és cosx szerepét felcserélve, hogy cosx sem lehet negatív.
Ha sinx≥0, cosx≥0, akkor ‐ mivel 0 és 1 közti szám nem kisebb, mint a négyzete ‐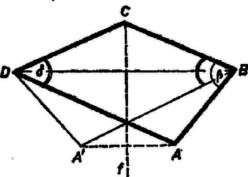
sinx+cosx+sinxcosx≥sinx+cosx≥sin2x+cos2x=1.
Itt mindenütt az egyenlőség jelének kell fennállnia ahhoz, hogy (1) teljesüljön. Az első esetben akkor áll egyenlőség, ha vagy sinx=0 ‐ és ekkor cosx≥0 folytán, cosx=1 ‐, vagy cosx=0, sinx=1. Ezekben az esetekben (1) valóban fenn is áll, tehát megtaláltuk az egyenlet összes megoldását. A megfelelő szögértékek:
x=k⋅360∘,(k=0,±1,±2,...)ésx=90∘+k⋅360∘(k=0,±1,±2...).

 
II. megoldás. Vigyük át a bal oldal harmadik tagját a jobb oldalra és emeljünk négyzetre
sin2x+cos2x+2sinxcosx=1-2sinxcosx+sin2xcos2x.
A bal oldal első két tagjának az összege 1, így az egyenlet a következő alakba rendezhető át:
sinxcosx(4-sinxcosx)=0.
Az utolsó tényező értéke legalább 3, így az egyenlet csak úgy teljesülhet, ha sinx=0, vagy cosx=0. Ezeket (1)-be írva kapjuk, hogy cosx=1, ill. sinx=1 kell legyen. Ilyen x szögek valóban vannak is:
x=k⋅360∘(k=0,±1,±2,...),ill.x=90∘+k⋅360∘(k=0,±1,±2,...).

 
2. feladat Az ABCD konvex négyszögben BC=CD. Adottak az AB és AD oldalak, továbbá a B és D csúcsnál levő szögek. Szerkesszük meg a négyszöget.
 
Megoldás. Legyen ABCD egy a követelményeknek megfelelő négyszög. A betűzést válasszuk úgy, hogy AB≤AD legyen. A B-nél és D-nél levő szög legyen β, illetve δ. Tükrözzük a négyszöget a BD átló felező merőlegesére. Ekkor C helyben marad, B és D egymás tükörképei. Legyen A tükörképe A', ezek különbözők, ha AB≠AD. Ezt egyelőre feltesszük. Az AA'B háromszögben ismert az AB és A'B=AD oldal, továbbá a köztük levő szög, mint β és δ különbsége. Ebből az AA'B háromszög és abból a négyszög megszerkeszthető, pl. a következő módon. Egy B csúcsú, |β-δ| nagyságú szög száraira rámérjük az adott BA és BA'=DA hosszúságokat. Húzzuk meg az AA' szakasz f felező merőlegesét; mérjük az AB oldalra B végpontjában a β szöget. E szög A-t nem tartalmazó szárának f-fel való metszéspontja adja C-t, B-nek f-re vonatkozó tükörképe D-t.
 
 

1. ábra
 

A szerkesztés az AB<AD esetben csak akkor adhat a feltételeknek megfelelő négyszöget, ha β>δ. Ugyanis AD=A'B>AB folytán A és B ugyanazon a partján van f-nek, D az ellenkezőn, így az AD és A'B szakaszok metszik egymást f-en; más szóval BA' metszi az AD oldalt, s így az ABC konvex szögtartományban halad, tehát
δ=A'BC∢<ABC∢=β.
Ha ez teljesül, és a szerkesztés elvégezhető, akkor egy négyszöget kapunk, és ennek oldalai és szögei a kívánt tulajdonságúak: BC=CD teljesül, és AD=A'B a kívánt nagyságú, ABA'∢=β-δ, így ABC∢=β mellett
ADC∢=A'BC∢=ABC∢-ABA'∢=β-(β-δ)=δ
is a kívánt nagyságú. Nem föltétlenül lesz azonban konvex a négyszög.
Az is lehet, hogy a szerkesztés egy C pontot sem ad, ha ugyanis β-nak az A-t nem tartalmazó szára párhuzamos f-fel, vagy a meghosszabbítása metszi f-et. A feladatnak tehát akkor van megoldása és csak egy, ha a β szög A-t nem tartalmazó szára metszi az f egyenest, éspedig a BD egyenes ellenkező oldalán, mint amelyiken A van. Az egyes lehetőségek feltételeit az adatokra vonatkozó összefüggésekkel fejezni ki igen körülményes és bonyolult számítási feladatot igényelne.
Ha AB=AD, akkor a négyszög deltoid, tehát β=δ kell hogy teljesüljön, ha pedig ez fennáll, akkor végtelen sok négyszög kielégíti a feltételt. Ugyanis egy β nagyságú szög egyik szárára rámérjük a B csúcsból a BA távolságot, a másik száron kijelölünk tetszés szerint egy C pontot, ha β nem hegyes szög, ha pedig hegyes szög, akkor C-t A-nak a száron levő vetületénél messzebb választjuk a csúcstól, végül vesszük a B pont D tükörképét AC-re. Az ABCD deltoid konvex és AB, AD oldala, továbbá B-nél és D-nél levő szöge a kívánt nagyságú. Ekkor tehát a feladat határozatlan.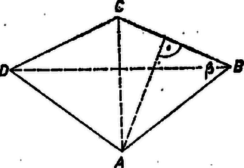
 
 

2. ábra
 

Megjegyzés. Többen háromszögnek egy oldalából, a rajta fekvő egyik szögből és a másik két oldal összegéből való megszerkesztésére vezették vissza tükrözéssel a feladatot. Ennek megoldása viszont megint csak lényegében a fenti AA'B háromszög megszerkesztésére vezet.
 
3. feladat. Egy 6×6 mezőből álló ,,sakktáblát'' hézagmentesen és átfedés nélkül dominólapokkal fedtünk be. Mindegyik dominólap két szomszédos mezőt takar le. Bizonyítandó, hogy a mezőket elválasztó 5 vízszintes és 5 függőleges vonal között van olyan, amely egyetlen dominólapot sem vág ketté.
 
I. megoldás. Megkíséreljük rendszeres próbálgatással a kívánt módon lefedni a táblát és látni fogjuk, hogy ez nem sikerül. Hogy könnyebben tudjuk magunkat kifejezni ‐ a sakkhoz hasonlóan ‐ az oszlopokat az a-f betűkkel, a sorokat az 1-6 számokkal fogjuk jelölni, a dominókat az általuk lefedett mezők megjelölésével, pl. (b-c, 4) dominó, (c, 1-2) dominó. Az előbbivel párhuzamos dominókat vízszintesnek, az utóbbival párhuzamosakat függőlegesnek fogjuk mondani. Rajzban a mezőket középpontjaikkal jelöljük, a dominókat az általuk lefedett mezők középpontjainak összekötésével.
I. Tekintsük először a tábla sarkait lefedő dominókat. Lehet, hogy van két szomszédos sarok, amelyeket egy sorba vagy egy oszlopba eső dominók fednek le. Ekkor feltehetjük, hogy ezek az (a-b, 1), (e-f, 1) dominók, mert a középpont körüli elforgatással minden más helyzet átvihető ebbe. Az 1. és 2. sort elválasztó vonal ‐ vagy röviden 1-2 vonal ‐ ez esetben csak a c vagy d oszlopba helyezett dominót vághat ketté, és ha az egyikben kettévág egy dominót, akkor a másiknak az 1. sorbeli mezeje is csak függőleges dominóval fedhető le. (Az ábrákon a dominókat az (a-b, 1) dominótól kezdve egy folytonos vonallal áthúztuk helyzetük megállapításának sorrendjében.) A 2-3 vonal vagy az a és b, vagy az e és f oszlopok egyikében kell, hogy átvágjon egy dominót. Szimmetria miatt feltehető, hogy az első két oszlop egyikében átvág egyet, s ekkor ismét a másik oszlop 2. sorbeli mezeje is csak függőleges dominóval fedhető.
Fedjük most az a6 mezőt függőleges dominóval, ekkor a4-et vízszintessel kell. A b-c vonalnak az 5. és 6. sorban kell egy-egy vízszintes dominón áthaladnia (ismét úgy értve, hogy ha bármelyikben átszel egy vízszintes dominót, a másikban is át kell szelnie egyet; hasonló okoskodást a továbbiakban nem részletezünk). A c-d vonal ekkor a 3. és 4. sorban metsz át egy-egy dominót, a d-e vonal az 5. és 6. sorban; az f6 sarokmezőt ekkor függőleges dominóval kell fedni, így azonban a 4-5 vonal nem metsz át dominót.
II. Fedjük most az első 6 dominó előzőek szerinti elhelyezése után a6-ot vízszintes dominóval, ekkor a b-c vonal a 4. és 5. sorban metsz dominót, mivel bármelyikbe helyezve egyet az (a, 4-5) dominó szükségessé válik. Ekkor c3-at és c6-ot egy-egy vízszintes dominóval kell fedni, így a d-e vonal a 4. és 5. sorban metsz egy-egy dominót és e6-ot ismét vízszintes dominó fedi. Így azonban az 5-6. vonal nem metsz már át egyetlen dominót sem. Olyan lefedés tehát nincs, amelyikben valamelyik szélső sor vagy oszlop tartalmazná a két szélső mezejét lefedő dominókat.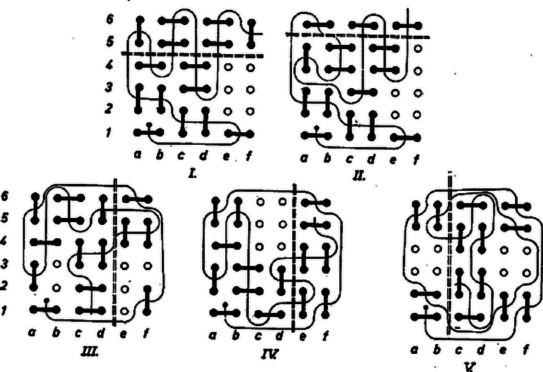
 
 

3. ábra
 

III. Egy átlóra való tükrözéssel ‐ ha kell ‐ elérhetjük, hogy a1-et vízszintes dominó fedje. Ekkor f1-et függőleges, f6-ot vízszintes, a6-ot ismét függőleges dominó kell, hogy fedje. Vizsgáljuk először az olyan lefedéseket, amelyekben valamelyik sarokdominóhoz a tábla szomszédos széle mentén rá merőleges dominó csatlakozik. Egy forgatással elérhetjük, hogy a2-t fedje függőleges dominó, ekkor a4-re vízszintes kerül. Fedjük továbbá b6-ot vízszintes dominóval, mikor is b5-re vízszintes, d6-ra függőleges dominó kerül. Ekkor a 4-5 vonalnak az e és f oszlopban, a 3-4 vonalnak pedig a c és d oszlopban kell dominót átmetszenie. Ezután a c-d vonal az 1. és 2. sorban metszhet csak át egy-egy dominót, a d-e vonal pedig nem metsz át egyet sem.
IV. Hagyjunk a sarokdominók III. szerinti elhelyezése után a2-n függőleges dominót és helyezzünk b6-ra is függőlegest. Közben a4-et ismét vízszintes dominóval kellett fedni, így a b-c vonal a 2. és 3. sorban metsz át egy-egy dominót, minek következtében c1-et vízszintes, e1-et, majd d2-t függőleges dominóval kell fedni. A 3-4 vonal ekkor az e és f oszlop egy-egy dominóját szeli át, és szerepelnie kell az (e-f, 5) dominónak. Így azonban a d-e vonal ismét nem metsz át dominót.
Ezzel kizártuk az összes olyan lefedéseket is, amelyekben a sarkokat III. szerint fedve le, a lefedő dominóhoz a tábla másik oldala mentén merőlegesen álló dominó csatlakozik.
V. Az olyan lefedéseket kell még vizsgálnunk, amelyekben a sarokmezők III. szerint vannak lefedve, továbbá a2-t és f5-öt vízszintes, 1-et és b6-ot függőleges dominó fedi. A 2-3 és 4-5 vonal két-két c és d oszlopbeli dominót kell, hogy átmessen, és szükség van a (c-d, 1), (c-d, 6) dominókra, ez esetben azonban a b-c és d-e vonal már nem metsz dominót.
Ezzel minden lehetséges úton megkíséreltünk olyan lefedést készíteni, amelyben minden vonal átmetsz legalább egy dominót, így meggyőződtünk róla, hogy ilyen lefedés nem lehetséges, a feladat állítása tehát helyes.
 
II. megoldás. Igen rövid úton célhoz érhetünk próbálgatás helyett egy kis okoskodással.
Bármely két sort vagy oszlopot elválasztó vonal két olyan részre vágja a táblát, amelyek mindegyike páros számú mezőt tartalmaz (hiszen ez minden sorra, ill. minden oszlopra külön is áll). Ha egy dominót úgy helyezünk el, hogy a kiszemelt vonal átmesse, akkor mindkét részben páratlan számú fedetlen mező marad, ezek csak úgy fedhetők le, ha legalább még egy dominó (és mindig páros számú) a vonal mindkét oldalán fed egy-egy mezőt. Így minden vonalnak legalább 2-2 dominót kell átmetszenie.
A táblát 6⋅6/2=18 dominó fedi le. Másrészt a sorokat is, az oszlopokat is 5-5 vonal választja el; ahhoz, hogy ezek mindegyike átmessen legalább 2 dominót, legalább 20 dominóra lenne szükség, annyi pedig nincs, tehát nem metszhet át minden elválasztó vonal dominót.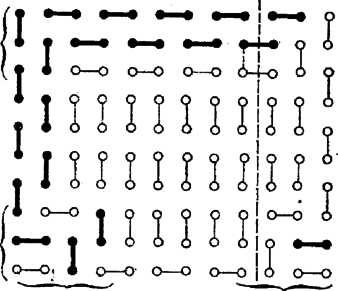
 
Megjegyzés. A II. megoldás gondolatmenete messzemenő általánosítást tesz lehetővé. Tekintsünk egy u×v mezőből álló táblát. Ha u is, v is páratlan, a tábla nyilván nem fedhető le hézagtalanul és átfedés nélkül dominókkal. Ha u is, v is páros, akkor a fenti gondolatmenet azt adja, hogy legfeljebb akkor lehet a feladat megoldható, ha
2(u-1+v-1)≤uv2,vagyis(u-4)(v-4)≥8.
Ha u páratlan, v páros, akkor az u hosszúságú sorok választó vonalai közül a szélsőtől kezdve minden második páratlan számú dominót metsz át, a többi páros számút, a v hosszúságú sorok választó vonalai mind páros számú dominót metszenek át, amiből
(u-3)(v-4)≥4
adódik szükséges feltételül. Ebből következik, hogy ha u vagy, v legfeljebb 4, akkor soha sincs kívánt lefedés, továbbá nincs a feladatban szereplő 6×6-os táblára.
 
 
4. ábra
 

A 4. ábráról leolvasható, hogy mindazokban az esetekben, amelyeket eddigi meggondolásaink nem zártak ki, lehetséges olyan lefedés, amelyben minden választó vonal átmetsz dominót. Az ábra olyan táblát mutat, amelynek páros számú sora és oszlopa van. Minden vonal átmetsz egyet a vastagabban jelölt dominók közül. Világos, hogy a középtájt elhelyezkedő azonos szerkezetű sorok és oszlopok száma tetszés szerinti páros számmal növelhető. A tábla szélein kapoccsal ({) megjelölt soroknak és oszlopoknak azonban mindig szerepelniük kell, a legkisebb így lefedhető táblának tehát a 8×6 mezős adódik.
Ha elhagyjuk a szaggatott vonaltól jobbra eső 3 oszlopot, akkor két mező, amelyeket ezen a vonalon átnyúló dominó fedett (a 2. és 3. sorban), lefedhető egy függőleges dominóval (az ábra pontozva jelzi). Így páratlan számú oszlopból és páros számú sorból álló táblák lefedését kapjuk. Ismét csak az a lényeges, hogy a kapoccsal megjelölt sorok és oszlopok fellépjenek, a legkisebb ilyen módon lefedhető tábla tehát 5×6 mezős. Az 5×6-os és 7×6-os tábla lefedhetősége kiemeli a feladat állításának sajátos helyzetét.
 
Surányi János