Kezdőlap


Cím:	Az 1963. évi Országos Középiskolai Matematikai Tanulmányi Verseny I. fordulóján kitűzött feladatok megoldása
Szerző(k):	Lukács Ottó , Surányi János
Füzet:	1963/november, 97 - 102. oldal	PDF \| MathML
Témakör(ök):	OKTV

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

1. feladat. Egy egyenlő szárú trapéz párhuzamos oldalainak hossza $a$ és $b$ , egyik szára felezőpontjának a másik szárra való vetülete ennek a szárnak egyik végpontjába esik. Számítsuk ki a trapéz területét.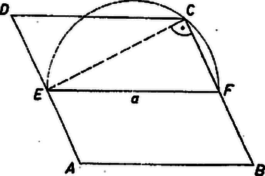

Megjegyzés: Egyenlő szárú trapézon olyant szokás érteni, amely szimmetrikus a párhuzamos oldalakra merőleges tengelyre nézve, és az alábbiakban mi is ezt fogjuk érteni rajta. Az elnevezés jelentése szerint minden paralelogramma is trapéz egyenlő szárakkal (és egyenlő párhuzamos oldalakkal). Így ha

a = b

, és a paralelogrammákat is tekintetbe vesszük, akkor egy

a

hosszúságú

E F

szakasz mint átmérő fölé rajzolt félkör bármely pontjából mint egyik csúcsból rajzolva olyan paralelogrammát, amelyiknek

E F

középvonala, a feltételeknek megfelelő, ,,egyenlő szárú trapéz''-t kapunk, a terület tehát határozatlan. Így csak érdektelen eseteket zártunk ki. Az

a = b

esetet is kizárhatjuk, mert ebben az esetben az elfogadott értelmezés mellett trapézunk téglalap, és így mindegyik oldal felezőpontjának vetülete a szemben levő oldalon annak a felezőpontja.

1. ábra

I. megoldás. Ha

a

-t és

b

-t ismerjük, akkor elég a magasság meghatározása a terület kiszámításához. Ehhez tájékozódunk először a trapéz alakjáról. Legyen a

D A

szár felezőpontja

E

, vetülete a

B C

száron a

C

csúcs. Ekkor

E

B C D

szögtartomány belsejében van, s így

\begin{matrix} D C B ∢ > E C B ∢ = 90^{\circ}, \end{matrix}

tehát

C

-nél és a szimmetria folytán

D

-nél is tompa szög van. Így, ha

a > b

, akkor

A B = a

C D = b

.
Tükrözzük a

C D E

háromszöget az

E

pontra. Ekkor a

D

pont

A

-ba kerül,

C

pedig a

C E

és

B A

szakaszok meghosszabbításainak

C'

metszéspontjába. Így a trapéz

t

területe egyenlő a

B C C'

derékszögű háromszögével. Jelöljük a

C

pont vetületét

A B

-n

M

-mel és

C M

-et

m

-mel, így

\begin{matrix} t = \frac{B C' \cdot m}{2}, \end{matrix}

és, felhasználva a derékszögű háromszög magasságának mértani közép tulajdonságát,

\begin{matrix} m^{2} = B M \cdot C' M, ahol B C' = a + b . \end{matrix}

B M

meghatározására tekintsük a

D

pont

N

vetületét is az

A B

oldalon. Egyrészt

M N = b

, másrészt a szimmetria miatt

A N = B M

és mivel a kettő együtt a párhuzamos oldalak különbségét adja, így

\begin{matrix} B M = \frac{a - b}{2}, C' M = a + b - \frac{a - b}{2} = \frac{a + 3 b}{2}, \\ m = \frac{\sqrt[]{(a - b) (a + 3 b)}}{2}, \end{matrix}

és a trapéz területe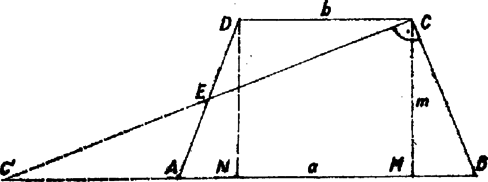

\begin{matrix} t = \frac{(a + b) \sqrt[]{(a - b) (a + 3 b)}}{4} . \end{matrix}

2. ábra

II. megoldás. Az

m

magasság meghatározására vegyük figyelembe, hogy a trapéz szimmetriája folytán a

B C

szár

F

felezőpontjának az

A D

száron a vetülete a

D

csúcs, a

C E F

és

D F E

derékszögű háromszögek egybevágók. Tükrözzük a

C E F

háromszöget

E F

-re. Mivel a középvonal

A B

-től és

C D

-től egyenlő távol fut, velük párhuzamosan, így

C

tükörképe az

A B

-n levő

M

vetülete. A

D E M F

négyszög szemben fekvő oldalai egyenlők, így a négyszög paralelogramma, éspedig téglalap, mert

D

-nél (és

M

-nél) levő szögéről tudjuk, hogy derékszög. Ennek folytán átlói egyenlők:

D M = E F = (a + b) / 2

, és a

C D M

derékszögű háromszögből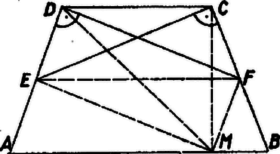

\begin{matrix} m^{2} = C M^{2} = D M^{2} - C D^{2} = {(\frac{a + b}{2})}^{2} - b^{2} = \frac{(a + 3 b) (a - b)}{4} . \end{matrix}

Megjegyzés: Több más út is választható

m

meghatározására, vagy kiszámíthatjuk a

B C

szár hosszát és annak ismeretében az I. megoldásban szereplő

B C C'

háromszög

C C'

befogóját, a területet pedig a

t = B C \cdot C C' / 2

összefüggésből. A fenti két számítás látszik még legegyszerűbbnek.

3. ábra

2. feladat. Egy kétjegyű számhoz adjuk hozzá számjegyeinek összegét, majd az így nyert számhoz újra adjuk hozzá számjegyeinek összegét. Így olyan kétjegyű számhoz jutunk, melynek jegyei az eredeti szám jegyei, fordított sorrendben. Melyik ez a szám?

I. megoldás. Jelöljük a keresett számot így:

N = \bar{x y} = 10 x + y

, itt

x \geq 1

, mert a szám kétjegyű. Hozzáadva

N

-hez a számjegyek

x + y

összegét az

\begin{matrix} N_{1} = 10 x + y + (x + y) = 11 x + 2 y \end{matrix}

összeg utolsó jegye az

M = x + 2 y

szám utolsó jegye lesz, első jegye pedig

x

-nél

M

tízes jegyével nagyobb. Jelöljük ezt a jegyet

k

-val, erre

0 \leq k \leq 2

, mert

M \leq 3 \cdot 9 = 27

M

és vele együtt

N_{1}

utolsó jegye

M - 10 k = x + 2 y - 10 k

N_{1}

első jegye

x + k

, így

N_{1}

jegyeinek összege

x + k + x + 2 y - 10 k = 2 (x + y) - 9 k

. Ezt

N_{1}

-hez adva a keletkező

N_{2}

számnak a jegyek felcserélésével keletkező

10 y + x

számnak kell lennie:

\begin{matrix} N_{2} = 11 x + 2 y + 2 (x + y) - 9 k = 13 x + 4 y - 9 k = 10 y + x . \end{matrix}

Innen

\begin{matrix} 6 y + 9 k = 12 x, 2 y + 3 k = 4 x . \end{matrix}

Itt

3 k

és vele együtt

k

is csak páros lehet, tehát

k

értéke

0

vagy

2

.
Ha

k = 0

, akkor

y = 2 x

N

jegyeinek összege

x + 2 y = 5 x

egyjegyű, tehát

x = 1

y = 2

, és

N = 12

megfelel a feladat feltételeinek, mert

\begin{matrix} N_{1} = 12 + 1 + 2 = 15, N_{2} = 15 + 1 + 5 = 21. \end{matrix}

k = 2

y = 2 x - 3

N

jegyeinek összegére

\begin{matrix} 20 \leq x + 2 y \leq 3 \cdot 9 = 27, 20 \leq 5 x - 6 \leq 27, 26 \leq 5 x \leq 33. \end{matrix}

Eszerint csak

x = 6

lehetséges, így

y = 9

, és

N' = 69

szintén megoldása a feladatnak, mert rá

N'_{1} = 69 + 6 + 9 = 84

N'_{2} = 84 + 8 + 4 = 96.

II. megoldás. Jelöljük a keresett

10 x + y

számból a jegyei hozzáadásával keletkező szám jegyeit

a

b

-vel:

\begin{matrix} 10 x + y + x + y = 11 x + 2 y = 10 a + b . \end{matrix}

Feltétel szerint ehhez hozzáadva jegyeit a

10 y + x

számot kapjuk:

\begin{matrix} 10 a + b + a + b = 11 a + 2 b = 10 y + x . \end{matrix}

A két összefüggésből kiküszöböljük

x

-et:

\begin{matrix} 11 (10 y + x) - (11 x + 2 y) & = 108 y \\ = 11 (11 a + 2 b) - (10 a + b) = 111 a + 21 b . \end{matrix}

Innen

\begin{matrix} 36 y = 37 a + 7 b, y = a + \frac{a + 7 b}{36} . \end{matrix}

Itt az utolsó tört számlálója osztható kell hogy legyen 36-tal, mert

y

egész, továbbá

a

legfeljebb 8, mert

y

nála nagyobb és számjegy. Így

a + 7 b \leq 8 + 7 \cdot 9 = 71

, tehát

a + 7 b = 36

kell hogy legyen. Innen

\begin{matrix} b = 5 - \frac{a - 1}{7} . \end{matrix}

Ez csak úgy lehet egész, ha

a - 1

osztható 7-tel, ami a számjegyek közül csak

a = 1

és

a = 8

-ra következik be;

b

megfelelő értékei 5 és 4. A keresett szám jegyeinek felcserélésével keletkező szám ekkor

11 a + 2 b = 21

, ill. 96, a keresett szám tehát 12 és 69 lehet, és mindkettő kielégíti a feladat feltételeit.

III. megoldás. Megmutatjuk, hogy a keresett szám 3-mal osztható. Legyen ugyanis a szám maradéka 9-cel osztva

r

, akkor, mint tudjuk, jegyeinek összege is

r

maradékot ad 9-cel osztva, s így a jegyek hozzáadásával keletkező szám ugyanannyi maradékot ad 9-cel osztva, mint

2 r

, és ugyanennyi maradékot ad a jegyeinek összege is. Ha tehát a keletkezett számhoz újra hozzáadjuk a jegyeinek összegét, az így kapott szám ugyanannyi maradékot ad 9-cel osztva, mint

4 r

. Másrészt ez a szám a keresett számból a jegyek felcserélésével kapható, tehát ugyanannyi maradékot ad 9-cel osztva, mint az:

r

-et. Így

4 r

-et 9-cel osztva a maradék

r

, vagyis

3 r

osztható 9-cel,

r

osztható 3-mal, tehát a keresett szám is.
Másrészt korlátokat keresünk a szám jegyeire. A keresett számot

10 x + y

-nal jelölve a kétszeri hozzáadással keletkező szám, amely a jegyek felcserélésével írható,

10 y + x

, a növekedés

\begin{matrix} 10 y + x - (10 x + y) = 9 (y - x) . \end{matrix}

Ez egyrészt 9-cel osztható, másrészt pozitív, tehát

x < y

. Ez a növekedés a keresett számból 4 számjegy hozzáadásával keletkezik, melyek közt van legalább két különböző (

x

és

y

), így összegük legfeljebb

3 \cdot 9 + 8 = 35

lehet, tehát

\begin{matrix} 9 (y - x) \leq 35, így y - x \leq 3, \end{matrix}

a keresett szám jegyeire tehát

\begin{matrix} x < y \leq x + 3. \end{matrix}

Ilyen tulajdonságú kétjegyű, 3-mal osztható számok a következők:

\begin{matrix} 12, 24, 36, 45, 57, 69, 78. \end{matrix}

Ezeket kipróbálva adódik, hogy 12 és 69 a feladat megoldásai.

3. feladat. Egy téglatest egy csúcsába összefutó három élének hossza

a

b

c

. Állítsunk merőleges síkot mindegyik csúcsán át az oda befutó testátlóra és tekintsük azt a konvex testet, amelyet az így kapott síkok bezárnak. Mennyi e test felszíne és térfogata?

Megoldás. Jelöljük a tégla csúcsait

A

B

C

D

E

F

G

H

-val (

A B C D

egy határlap és

A E ‖ B F ‖ C G ‖ D H

);

a

b

c

legyen rendre az

A B

A D

A E

élek hossza. A testátlók hosszát jelöljük

d

-vel, a tégla középpontját

O

-val; tudjuk, hogy

d^{2} = a^{2} + b^{2} + c^{2}

.
Állapítsuk meg először az átlókra merőleges síkok közt keletkező

T

test alakját. Az

A B

A D

A E

élek

T_{1}

T_{2}

T_{3}

felező merőleges síkjaira tükrözve a téglát, az önmagába megy át, testátlói ismét testátlókba, így az azokra merőleges síkok is egymásba mennek át, tehát a

T

test is szimmetrikus

T_{1}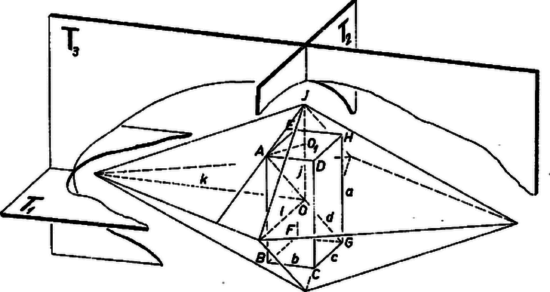

T_{2}

T_{3}

-ra.

4. ábra

A szimmetriasíkok létesítette térnyolcadok mindegyike egy téglacsúcsot tartalmaz. Az ebben a megfelelő testátlóra merőlegesen állított sík a szimmetriasíkokkal egy-egy 3-oldalú gúlát határoz meg, melynek egyik csúcsa

O

, és az ebben találkozó lapjai, amelyek a szimmetriasíkokban vannak, páronként merőlegesek. A testátlóra merőleges sík valóban a szimmetriasíkok metszésvonalainak a térnyolcadot határoló félegyeneseit metszi, mert a testátló átmegy

O

-n, ami a félegyenesek közös pontja és hegyes szöget alkot a félegyenesekkel. Egy ilyen gúla a szimmetriasíkokra való tükrözéssel sorra átvihető az összes többibe, és a 8 gúla együttesen alkotja

T

-t, amelynek határfelülete így 8 egybevágó háromszögből áll, élei a szimmetriasíkokban vannak, csúcsai ezek metszésvonalain.
Könnyű belátni (ezt számításainkban nem fogjuk felhasználni), hogy az egy szimmetriasíkban levő élek egy-egy rombuszt alkotnak, ezen mint alapon nyugvó két egyenes gúlából tevődik össze

T

. Az ilyen testet a kristálytanban rombos bipiramisnak nevezik.

T

térfogata a szimmetriasíkok közti egy nyolcadba eső háromoldalú gúla térfogatának 8-szorosa, felszíne pedig a téglacsúcson átmenő határlap

t

területének 8-szorosa. Jelöljük a szóban forgó gúlának a tégla

A B

A D

A E

éleivel párhuzamos éleinek hosszát

j

k

l

-lel, akkor térfogatát kétféle úton is kiszámíthatjuk: mint a merőleges élek hossza szorzatának a hatodát, és mint

t

-nek és a rá merőleges téglaátló felének

1 / 3

-szoros szorzatát:

\begin{matrix} \frac{1}{6} j k l = \frac{1}{6} d \cdot t . \end{matrix}

Így

T

térfogatára,

V

-re, ill. felszínére,

F

-re

\begin{matrix} V = \frac{8}{6} j k l = \frac{4}{3} j k l és F = 8 t = 8 \frac{j k l}{d}, \end{matrix}

tehát a kettő között a következő összefüggés áll fenn:

\begin{matrix} F = \frac{6 V}{d} . \end{matrix}

Elég tehát

F

és

V

egyikét meghatározni.

V

-t lesz könnyebb, illetőleg a kiszámításához szükséges

j

k

l

szakaszokat.
Jelöljük az

A

-t tartalmazó térnegyedbe eső gúla

j

hosszúságú élének

O

-tól különböző végpontját

J

-vel, az él metszéspontját az

A D H E

lappal (e lap középpontját)

O_{1}

-gyel. Ekkor

O O_{1} = a / 2

, továbbá

J A

O A

-ra

A

-ban emelt merőleges sík egy egyenese, s így merőleges

O A

-ra. Az

A J O

és

O_{1} A O

derékszögű háromszögek hasonlók, mert

O

-nál levő hegyesszögük közös; így

\begin{matrix} \frac{j}{d / 2} = \frac{O J}{O A} = \frac{O A}{O O_{1}} = \frac{d / 2}{a / 2}, j = \frac{d^{2}}{2 a} = \frac{a^{2} + b^{2} + c^{2}}{2 a} . \end{matrix}

Ugyanígy látható, hogy

\begin{matrix} k = \frac{d^{2}}{2 b}, l = \frac{d^{2}}{2 c} . \end{matrix}

Így a keresett mennyiségek

\begin{matrix} V = \frac{4}{3} \cdot \frac{d^{6}}{8 a b c} = \frac{1}{6} \cdot \frac{{(a^{2} + b^{2} + c^{2})}^{3}}{a b c}, \\ F = \frac{6 V}{d} = \frac{d^{5}}{a b c} = \frac{{(\sqrt[]{a^{2} + b^{2} + c^{2}})}^{5}}{a b c} . \end{matrix}

Lukács Ottó, Surányi János