Kezdőlap


Cím:	Az 1963. évi Arany Dániel matematikai tanulóversenyek I. fordulóján kitűzött feladatok megoldása: Haladók (II. osztályosok) versenye
Szerző(k):	Lőrincz Pál
Füzet:	1963/november, 107 - 109. oldal	PDF \| MathML
Témakör(ök):	Arany Dániel

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Haladók (II.osztályosok) versenye

1. feladat. Adott egy negyedkör, amelyet az

O A

és

O B

sugarak határolnak. Húzzunk az

A B

húrral párhuzamos, a negyedkört metsző egyenest és jelöljük ennek a negyedkörrel alkotott egyik metszéspontját

C

-vel, az

O A

és

O B

félegyenesekkel alkotott metszéspontjait pedig

P

-vel és

Q

-val. Bizonyítsuk be, hogy

\begin{matrix} A B^{2} = P C^{2} + Q C^{2} . \end{matrix}

(1)

I. megoldás. Elég megmutatni, hogy a megfelelő összefüggés fennáll a szóban forgó szakaszoknak az

O A

egyenesen levő vetületére. Ugyanis mindegyik vetület ugyanannyiad része (esetünkben

1 / \sqrt[]{2}

-szöröse) az eredeti szakasznak, és így a szakaszokat a vetületekkel helyettesítve (1) mindkét oldala ugyanazzal, a mondott arány négyzetével szorzódik.

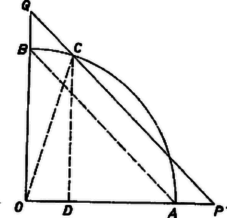1. ábra

A B

C P

C Q

szakaszok vetülete

A O = r

, (a kör sugara),

D P

és

D O

, továbbá, mivel a

C D P

háromszög egyenlő szárú, így

D P = D C

, tehát a vetületekre

\begin{matrix} D P^{2} + D O^{2} = D C^{2} + D O^{2} = O C^{2} = r^{2} = O A^{2}, \end{matrix}

mivel a

C D O

háromszög derékszögű. Fennáll tehát a bizonyítandó összefüggés is.

II. megoldás. Forgassuk el a kör középpontja körül a

Q P

szakaszt a

C

ponttal együtt

90^{\circ}

-kal úgy, hogy a

P

pont a

Q

pontba kerüljön, és az elforgatott

C

pontot jelöljük

C^{*}

-gal. Ekkor a

C^{*} C Q

háromszög

Q

-nál fekvő szöge derékszög, és

Q C^{*} = P C

. Másrészt a

C^{*} O C ∢ = 90^{\circ}

, így

C^{*} C = r \sqrt[]{2}

. Eszerint az (1) összefüggés éppen a

C^{*} C Q

derékszögű háromszögre felírt Pythagoras-tétel.

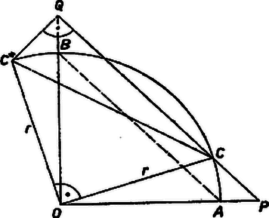2. ábra

Megjegyzés. Állításunk akkor is érvényes, ha megrajzolva a teljes

O

középpontú,

r

sugarú kört, az

A B

-vel párhuzamos szelő ezt a negyedkörön kívül eső

C

pontban metszi. Mindkét előbbi megoldás alkalmas ennek bebizonyítására is.

2. feladat. Bizonyítsuk be, hogy az

\begin{matrix} \frac{1}{a - b} + \frac{1}{b - c} + \frac{1}{c - a} \end{matrix}

kifejezés mindig pozitív, ha

a

b

és

c

különböző számok, és közülük az ,,

a

'' a legnagyobb, és a

c

pedig a legkisebb.

I. megoldás. A törteket közös nevezőre hozzuk és összeadjuk. Elvégezve a lehetséges összevonásokat nyerjük, hogy

\begin{matrix} \frac{1}{a - b} + \frac{1}{b - c} + \frac{1}{c - a} = \frac{a b + b c + c a - a^{2} - b^{2} - c^{2}}{(a - b) (b - c) (c - a)} . \end{matrix}

A jobb oldali tört számlálója ilyen alakban írható:

\begin{matrix} - \frac{1}{2} [{(a - b)}^{2} + {(b - c)}^{2} + {(c - a)}^{2}] . \end{matrix}

A szögletes zárójelben a négyzetösszeg pozitív, tehát maga a számláló negatív. De a nevező első két tényezője pozitív, a harmadik negatív, ezért a nevező szintén negatív, így a tört értéke pozitív.

II. megoldás. Az

a > b > c

kikötés miatt az első két tört pozitív, a harmadik negatív. A harmadik tört nevezőjének abszolút értéke

a - c = (a - b) + (b - c)

, az első két nevező összege; eszerint reciproka, vagyis a harmadik tag abszolút értéke kisebb

\frac{1}{a - b}

és

\frac{1}{b - c}

mindegyikénél, még inkább kisebb e két tört összegénél.

3. feladat. Bizonyítsuk be, hogy ha

\begin{matrix} p + q + r = 1 \end{matrix}

(2)

és

\begin{matrix} \frac{1}{p} + \frac{1}{q} + \frac{1}{r} = 0, \end{matrix}

(3)

akkor

\begin{matrix} a^{2} + b^{2} + c^{2} = {(p a + q b + r c)}^{2} + {(q a + r b + p c)}^{2} + {(r a + p b + q c)}^{2} . \end{matrix}

(4)

Megoldás. A jobb oldalon elvégezve a négyzetreemelést, a keletkező 9 négyzetes tag és 9 kettős szorzat így csoportosítható:

\begin{matrix} a^{2} (p^{2} + q^{2} + r^{2}) + b^{2} (p^{2} + q^{2} + r^{2}) + c^{2} (p^{2} + q^{2} + r^{2}) + & (5) \\ + 2 a b (p q + q r + r p) + 2 b c (p q + q r + r p) + 2 c a (p q + q r + r p) . \end{matrix}

A feltételi egyenlőségekből meghatározzuk a

p^{2} + q^{2} + r^{2}

négyzetösszeg és a

p q + q r + r p

szorzatösszeg értékét. Miután (3) értelmében

p

q

és

r

egyike sem nulla, (3)-at végigszorozhatjuk

p q r

-rel:

\begin{matrix} q r + r p + p q = 0. \end{matrix}

(6)

Továbbá emeljük négyzetre (2)-t:

\begin{matrix} p^{2} + 2 p q + q^{2} + 2 p r + 2 q r + r^{2} = 1. \end{matrix}

Ámde a bal oldalon a kettős szorzatok összege (6) szerint

0

, így

\begin{matrix} p^{2} + q^{2} + r^{2} = 1. \end{matrix}

(7)

(6) és (7) értékét behelyettesítve (5)-be, ott a négyzetes tagok együtthatója

1

, a kettős szorzatok pedig kiesnek, és így a kifejezés azonosan egyenlő (4) bal oldalával.

Lőrincz Pál