Cím: Az 1963. évi Arany Dániel matematikai tanulóversenyek I. fordulóján kitűzött feladatok megoldása: Kezdők (I. osztályosok) versenye
Szerző(k):  Lukács Ottó 
Füzet: 1963/október, 49 - 51. oldal  PDF  |  MathML 
Témakör(ök): Arany Dániel

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Kezdők (I. osztályosok) versenye

 
1. feladat. Két szám legkisebb közös többszöröse 19-cel nagyobb, mint a legnagyobb közös osztójuk. Mi lehet ez a két szám?
 
Megoldás. Keressük a pozitív egész megoldásokat. Jelöljük a keresett két szám legkisebb közös többszörösét t-vel, a legnagyobb közös osztót d-vel. A legkisebb közös többszörös osztható a számok mindegyikével, s így legnagyobb közös osztójukkal is, tehát a t-d különbség, ami a feladat feltétele szerint 19, osztható d-vel. Mivel 19 prímszám, (pozitív) osztója csak 1 és 19, csak ezek jönnek tehát tekintetbe d gyanánt.
Ha d=1, akkor t=1+19=20 a két keresett szám legkisebb közös többszöröse, és a számok relatív prímek, így a legkisebb közös többszörösük a szorzatuk. 20 két egymáshoz relatív prím tényezőre való felbontásai (a tényezők sorrendjétől eltekintve) 1⋅20 és 4⋅5, tehát 1, 20 és 4, 5 két megfelelő számpár.
Ha d=19, akkor t=38, így a két szám 19 többszöröse és 38 osztója, tehát 19 vagy 38. A két szám nem lehet egyenlő, mert akkor t-d=0 lenne, a 19, 38 számpár viszont megfelel a feladat feltételeinek. ‐ Így 3 pozitív egészekből álló számpár elégíti ki a feladat követelményeit.
Ha negatív egészeket is tekintetbe veszünk, akkor azok a számpárok felelnek meg, amelyek a fentiekből az egyik, vagy mindkét szám előjelének a megváltoztatásával keletkeznek, ugyanis egy számnak és a negatívjának ugyanazok a többszörösei és ugyanazok az osztói. Így két számnak a legkisebb közös többszöröse és legnagyobb közös osztója ugyanaz, mint a két szám abszolút értékéé.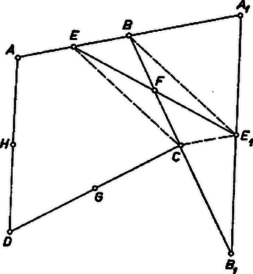
 
Megjegyzés. Sok versenyző csak felírt egy vagy két megoldást, vagy mind a hármat is, de minden indokolás nélkül. Ezek mellett lehetne a feladatnak még akárhány további megoldása is. Lényeges matematikai gondolatot éppen annak a belátása igényelt, hogy a fenti 3 számpár az összes megoldást megadja.
 
2. feladat. Adott egy ABCD négyszög. Tükrözzük A-t B-re, B-t C-re, C-t D-re, D-t A-ra, és legyenek a tükörképek rendre A1, B1, C1, D1. Járjunk el hasonlóan azzal a négyszöggel, melynek csúcsai sorra az AB, BC, CD, DA oldalak felezőpontjai. Bizonyítandó, hogy az így kapott tükörképek az A1B1C1D1 négyszög oldalainak felezőpontjai.
 
 

Megoldás. Elegendő az ABCD és az A1B1C1D1 négyszög egy-egy megfelelő oldalának, pl. az AB és A1B1 oldalnak az E és E1 felezőpontját összekötő szakaszról kimutatni, hogy az első négyszögnek a sorrendben következő, azaz a BC oldalával való F metszéspontja mindkét szakaszt felezi, hiszen ekkor F a BC oldal felezőpontja, és E1 az E-nek erre vonatkozó tükörképe.
A két szakasz akkor és csak akkor felezi egymást, ha a BECE1 négyszög paralelogramma. Ez viszont igaz, mert az E1C szakasz az A1B1B háromszög középvonala, így párhuzamos az A1B szakasszal és fele akkora. Ugyanekkora az A1B szakasz meghosszabbítását képező BE szakasz is, mert A1B az AB szakasz tükörképe. Így BE és E1C egy irányban párhuzamosak és egyenlők, tehát BECE1 valóban paralelogramma. Ezzel a feladat állítását bebizonyítottuk.
 

3. feladat. Egy üdülőben hárman közösen 30 db közönséges lottószelvényt töltöttek ki. Ehhez A 25, B 36 és C 38 Ft-ot adott. Több szelvénnyel találatot értek el, kézhez kaptak 1100 Ft-ot. Ebből a következő hétre 30 db hónapos (5 hetes) és 20 db 1 hetes szelvényt vettek, a maradó összeget pedig úgy osztották fel, hogy C 2-szer annyit kapott, mint B, és B 2-szer annyit, mint A. Ismét nyertek, 73000 Ft-ot kaptak kézhez. Tovább nem játszhattak együtt, ezért megállapodtak, hogy a második hét betéteinek arányában osztoznak, és hogy a továbbjátszó szelvényekből 10-et‐10-et vesznek át. Ki mennyi készpénzt kapott?
 
Megoldás. A játékosok együtt 99 Ft-ot fizettek be a 30 lottószelvényre. Az első heti 1100 Ft tiszta nyereségből a játékosokat betéteik arányában rendre a következő részek illetik meg:
A:25⋅110099=27779Ft,B:36⋅110099=400Ft,C:38⋅110099=42229Ft.

A második hétre vásárolt 30 db 5 hetes szelvény ára 30⋅5⋅3,30=495Ft, a 20 db közönséges szelvény ára 66 Ft, összesen 561 Ft, így 539 Ft-ot osztottak szét. A részek aránya 1:2:4, az arányszámok összege 7, ezért A 539:7=77Ft-ot kapott, B154Ft-ot, C pedig 308 Ft-ot.
Így az egyes játékosok részesedése az új szelvények árában a következő:
A:20079Ft,B:246Ft,C:11429Ft.
Ezek aránya:
1807:2214:1028,
és az arányszámok összege 5049. Ennek megfelelően kell felosztaniuk a második húzás utáni vagyonukat. Ez egyrészt a 73 000 Ft készpénzből áll, másrészt a 30 db továbbjátszó szelvényből, amelyek értéke 30⋅4⋅3,30=396Ft, mert még 4 hétre érvényesek. Így a részek, fillérre kerekítve:
A:1807⋅733965049=26267,89Ft,B:2214⋅733965049=32184,34Ft,C:1028⋅733965049=14943,77Ft.



Továbbjátszó szelvényekben mindegyikük 132 Ft értéket kapott, így készpénzrészesedésük:
A:26135,89Ft,B:32052,34Ft,C:14811,77Ft.

 
Megjegyzés. Sok versenyző azzal követett el kisebb hibát, hogy csak a 73 000 Ft-ot osztotta szét 1807:2214:1028 arányban, megfeledkezve a továbbjátszó szelvényekről, pedig ezek is a közös vagyon részét képezik. ‐ Többen viszont a szelvények árát felejtették el levonni az egyes játékosokra jutó teljes forint értékből.
 
 Lukács Ottó