Cím: 1962. évi Kürschák József matematikai tanulóverseny feladatainak megoldása
Szerző(k):  Hajós György 
Füzet: 1963/március, 98 - 109. oldal  PDF  |  MathML 
Témakör(ök): Kürschák József (korábban Eötvös Loránd)

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Első feladat. Legyen n egy természetes szám. Tekintsük az olyan u, v számpárokat, amelyekben u és v természetes számok, és legkisebb közös többszörösük n (ha u és v különböző, akkor az u, v számpárt a v, u számpártól különbözőnek tekintjük). Bizonyítsuk be, hogy az ilyen számpárok száma megegyezik n2 pozitív osztóinak számával.

 

Megjegyzések. 1. A feladat szövegének zárójelbe foglalt kiegészítése más szóval azt jelenti, hogy nem olyan u, v számpárok számát vizsgáljuk, amelyekben a két szám sorrendje közömbös, hanem az u, v rendezett számpárokét, hogy tehát az összeszámláláskor két számpár csak akkor tekintendő azonosnak, ha bennük az első számok és a második számok is egyenlők.
2. A feladat alábbi megoldásaiban használjuk a következő, általánosan is használt jelöléseket: természetes számok körében (a, b) az a, b számok legnagyobb közös osztóját, [a, b] a legkisebb közös többszörösüket, a|b pedig azt jelöli, hogy a osztója b-nek.
 

I. megoldás. Legyen n törzstényezős felbontása
n=p1a1p2a2...psas,
ahol p1,p2,...,ps különböző törzsszámok, a1,a2,...,as pedig nem-negatív egész számok. Minthogy a vizsgált számpárokra [u,v]=n, az u, v számok törzstényezői is csak a p1,p2,...,ps törzsszámok közül valók lehetnek.
Vizsgáljuk meg, hogy pl. p1 mekkora kitevővel szerepelhet u-ban és v-ben. E két kitevő között [u,v]=n miatt a1-nek is szerepelnie kell, és egyik sem lehet a1-nél nagyobb. Ez háromféleképpen következhetik be: 1. p1 kitevője mindkét helyen a1, ez 1 lehetőség;  2. p1 kitevője u-ban a1, v-ben viszont kisebb, tehát a 0,1,2,...,a1-1 számok valamelyike, ami a1 lehetőséget jelent; 3. p1 kitevője v-ben a1 és u-ban kisebb, ami ismét a1 lehetőséget ad. Az összes lehetőségek száma ezek szerint 2a1+1.
Hasonlót mondhatunk a többi törzstényezőről is. Minthogy pl. p1 kitevőinek rögzítése után a többi kitevő számára ugyanazok a lehetőségek maradnak meg, a vizsgált u, v számpárok száma az egyes törzstényezőkre számba vett lehetőségek szorzata:
(2a1+1)(2a2+1)...(2as+1).
Meg kell még mutatnunk, hogy n2 osztóinak száma ugyanennyi. Ez nyomban belátható abból, hogy
n2=p12a1p22a2...ps2as
osztóiban pl. p1 kitevője 0,1,2,...,2a1 lehet, azaz 2a1+1 lehetőség van, s hogy az így adódó lehetőségek számát ismét össze kell szorozni, hiszen az egyes törzstényezőkre vonatkozó lehetőségek egymástól ismét függetlenek.
 

Megjegyzés. Megoldásunkban az a kitevő 2a+1 lehetőséghez vezetett. Ehhez az értékhez a következő, bonyolultabb módon is eljuthatunk:
Az u-ban és v-ben szereplő kitevők egyike sem nagyobb a-nál, azaz mindkettő a 0,1,2,...,a értékek valamelyike. Eszerint a+1 lehetőség adódik mindegyik megválasztására, és (a+1)2 lehetőség a kitevőpár számára. E lehetőségek közül azonban csak azok felelnek meg, amelyekben legalább egyszer maga az a érték is szerepel. Ki kell tehát zárnunk azokat az eseteket, amelyekben mindkét kitevő a 0,1,2,...,a-1 számok közül való. Ez összesen a2 lehetőség kirekesztését jelenti, s ezért a tényleges lehetőségek száma (a+1)2-a2=2a+1.
Ez a bonyolultabb út azért tanulságos, mert magyarázat nélkül érthetővé teszi, hogy ha az u, v számpár helyett olyan u1,u2,...,uk számsorozatok számát keressük, amelyekben szereplő számok legkisebb közös többszöröse n, akkor feleletül
[(a1+1)k-a1k][(a2+1)k-a2k]...[(as+1)k-ask]
adódik.
 

II. megoldás. A feladat állítását azáltal bizonyítjuk, hogy a vizsgált u, v rendezett számpárok és n2 osztói között kölcsönösen egyértelmű hozzárendelést létesítünk. Az u, v számpárhoz azt a d számot rendeljük hozzá, amelyre
uv=dn.(1)
Ez a d valóban egész szám, mert [u,v]=n miatt v|n, s így a baloldali törtet egész számmal kell bővíteni, hogy a jobboldali alakot vegye fel. Ez azt is mutatja, hogy d valóban n2 osztója, hiszen az u számlálót n egy másik osztójával ti. n/v-vel szorozva adódik.
Fel fogjuk használni, hogy ha u1:v1=u2:v2, akkor
u1:u2=v1:v2=[u1,v1]:[u2,v2].(2)
Két szám legkisebb közös többszörösének keresésekor ugyanis két olyan, lehetőleg kicsiny egész számot kell keresnünk, amelyekkel az egyiket és a másikat megszorozva ugyanahhoz az eredményhez jutunk. Ezeknek az egész számoknak a megválasztása eszerint csak a megadott két szám arányától függ. Ha tehát az u1, v1 számpárról az ugyanolyan arányú u2, v2 számpárra térünk át, akkor ‐ miként állítottuk ‐ a legkisebb közös többszörös is velük arányosan változik meg.
Bebizonyítjuk most, hogy különböző u1, v1 és u2, v2 számpárokhoz nem tartozhat ugyanaz a d szám. Ha ez így volna, akkor rájuk
u1v1=u2v2=dn
s ennek következtében (2) is teljesülne. Minthogy pedig [u1,v1]=[u2,v2]=n, (2) szerint u1=u2 és v1=v2 adódik, ami állításunk helyességét bizonyítja.
Be kell még bizonyítanunk, hogy n2 minden d osztója szerepel az u, v számpárokhoz tartozó számok között. Ennek bizonyítása végett a d/n törtet redukált
dn=pq
alakra hozzuk, ahol tehát (p,q)=1. Elég bebizonyítanunk, hogy [p,q]|n, mert akkor (2) szerint a p/q tört olyan u/v törtté bővíthető, amelyre az [u,v]=n feltétel is teljesül.
Eszerint már csak p|n és q|n bizonyítása a feladatunk. Az utóbbi nyilvánvalóan helyes, hiszen q egy n nevezőjű tört egyszerűsítése után lépett fel nevezőként. A p-re vonatkozó állítás
n2d=nqp
következménye, mert itt a baloldalon egész szám áll, ezért a jobboldalon is, azaz p|nq. Minthogy pedig (p,q)=1, eredményünkből p|n is következik.
 

III. megoldás. Az előző megoldáshoz hasonlóan okoskodunk és ugyanúgy indulunk el. A vizsgált számpárokhoz ismét (1) előírásával rendeljük hozzá n2 egy-egy osztóját.
(1)-ből (2)-re hivatkozva
u:d=v:n=n:[d,n](3)
következik, hiszen [u,v]=n. Eszerint d ismeretében u és v már meghatározható:
u=dn[d,n],v=n2[d,n].(4)
n2 valamely d osztója tehát csak ehhez az egyetlen u, v számpárhoz tartozhatik hozzá.
Ha d|n2, akkor (4) egész számokat szolgáltat, hiszen dn és n2 egyaránt közös többszöröse a d, n számoknak, ezért legkisebb közös többszörösük egész számszorosa. Ha tehát n2 valamely d osztójából kiindulva (4) előírásával az u, v számpárt képezzük, olyan egész számokat kapunk, amelyekre a (4)-gyel egyenértékű (3) is teljesül, ami csak [u,v]=n esetén következhetik be. Ezek szerint n2 minden osztója szerepel az u, v számpárjainkhoz rendelt számok között.
 

Második feladat. Bizonyítsuk be, hogy egy konvex n-szög átlói közül nem lehet n-nél többet úgy kiválasztani, hogy bármely kettőnek legyen közös pontja.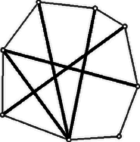
 
 
1. ábra
 

I. megoldás. Egy konvex n-szögben d átlót választunk ki úgy, hogy közülük bármely kettőnek legyen közös pontja (1. ábra). Két csúcsot akkor mondunk szomszédosnak, ha kiválasztott átló köti össze őket. Egy csúcs akkor i-edfokú, ha i csúccsal szomszédos. Az i-edfokú csúcsok számát ai-vel jelöljük. Ezek szerint
a1+a2+a3+...≤n,
hiszen a baloldal értéke akkor volna n, ha azoknak a csúcsoknak a számát is hozzáadnók, amelyeknek nincs szomszédjuk, azaz nem indul ki belőlük kiválasztott átló.
Ha valamely csúcs fokszáma i>2, akkor a belőle kiinduló kiválasztott átlók közül két ,,szélső'' közrefog egyet vagy többet. Az ilyen közrefogott átló másik végpontjában nem csatlakozhat hozzá kiválasztott átló, mert annak nem lehetne közös pontja a két ,,szélső'' mindegyikével. Eszerint i>2 esetén minden i-edfokú csúcs legalább i-2 elsőfokú csúccsal szomszédos. Minden elsőfokú csúcs természetesen csak legfeljebb egy magasabb fokú csúccsal lehet szomszédos. Ebből az elsőfokú csúcsok a1 számára
a1≥a3+2a4+3a5+...
következik, hiszen a harmadfokú csúcsok legalább egy-egy elsőfokúval szomszédosak, a negyedfokúak legalább kettővel-kettővel, stb.
A d darab kiválasztott átlónak összesen 2d vége van. Ezek a végek a csúcsoknál helyezkednek el, minden i-edfokú csúcsba i vég fut. Ezek szerint
2d=a1+2a2+3a3+4a4+...
Ebből az egyenletből az előzők felhasználásával
2d=(a1+2a2+2a3+2a4+...)+(a3+2a4+...)≤≤(a1+2a2+2a3+2a4+...)+a1==2(a1+a2+a3+a4+...)≤2n
következik. Bebizonyítottuk tehát, hogy valóban d≤n.
 

Megjegyzések. 1. Megoldásunk az átlókról csak azt használta ki, hogy azok a csúcsokat összekötő egyenes szakaszok. Változatlanul helyes marad tehát a megoldás, ha a sokszög oldalait is az átlói közé soroljuk, ha tehát azt bizonyítjuk, hogy egy konvex n-szög csúcsait összekötő szakaszok közül nem lehet n-nél többet úgy kiválasztani, hogy bármely kettőnek legyen közös pontja.
2. Csak ott gondoltunk arra, hogy egy konvex sokszög csúcsairól van szó, ahol a ,,közrefogott'' átlókról mondhattuk, hogy elsőfokú csúcsokba vezetnek. Itt sincs azonban erre szükség. Ha egy pontból más-más irányba három szakasz indul, akkor sohasem csatlakozhat mindegyikhez annak végpontjában olyan szakasz, amelynek a pontból kiinduló másik két szakasz mindegyikével van közös pontja. Ha ugyanis a három szakasz egy a ponton áthaladó egyenes által határolt félsíkban van, akkor nem mondtunk újat; ha viszont nem ez a helyzet, akkor a három szakasz egyikéhez sem csatlakozhat annak végpontjában olyan szakasz, amelynek van közös pontja a másik kettő mindegyikével. Ezek szerint azt is bebizonyítottuk, hogy ha a sík n pontja közül egy egyenesen sincs kettőnél több, akkor e pontokat összekötő szakaszok közül nem lehet n-nél többet úgy kiválasztani, hogy bármely kettőnek legyen közös pontja.
Szükség volt itt arra a megszorításra, hogy kettőnél több pont nincs egy egyenesen. Nemcsak azért, hogy bizonyításunk, amely más-más irányba induló szakaszokról szólt, alkalmazható legyen, hanem azért is, mert pl. egy egyenesen egymást követően felvett A, B, C, D pontok AB, AC, AD, BC, BD összekötő szakaszai már ellentmondanának a megszorítás nélkül kimondott állításnak.
3. Megemlítjük végül, hogy a most említett általánosítások ugyanúgy kiolvashatók a következő megoldásból is.
 

II. megoldás. Bebizonyítjuk, hogy ‐ miként megjegyzésünkben már említettük ‐ ha nemcsak az átlókból válogathatunk, hanem az oldalakból is, akkor sem választható ki n-nél több, páronként közös ponttal rendelkező szakasz.
Ha az n-szög csúcsai között van elsőfokú, tehát olyan, amelyből csak egy kiválasztott szakasz indul ki, akkor hagyjunk el ábránkból egy ilyen szakaszt. Eredetileg d szakasz szerepelt, és együttesen m≤n végpontjuk volt. Az elhagyás után csak d1=d-1 szakasz maradt, és végpontjaik száma is legalább 1-gyel kisebb: m1≤n-1.
Ha lehetséges, hagyjunk el ismét ugyanúgy egy szakaszt. Ezáltal d2=d-2 szakaszhoz jutunk, amelyek végpontszáma m2≤n-2. Folytassuk ezt, amíg csak lehetséges. Végül dk=d-k szakaszhoz jutunk, amelyeknek együttesen mk≤n-k végpontjuk van.
Az így kapott ábrában már nincs elsőfokú szögpont, de nincs 2-nél nagyobb fokszámú sem, mert ha egy csúcsból három szakasz is kiindul, akkor a ,,közrefogott'' szakaszok végpontja csak elsőfokú lehet, amint ezt az előző megoldásban is felhasználtuk. A végábrában ezek szerint minden végpont másodfokú. A szereplő dk szakasz 2dk vége tehát párosával esik egybe, azaz mk=dk pontba fut. Az mk=dk eredmény akkor is helyes, ha az elhagyogatások befejezése után egyetlen szakasz sem marad meg, mert akkor dk=0 és mk=0.
A dk=mk eredményből az előzők szerint d-k≤n-k, azaz d≤n következik, ami a feladat állítása volt.
 

III. megoldás. Közömbös, hogy melyik konvex n-szög átlói közül akarunk megfelelő módon lehető legtöbbet kiválasztani, hiszen két átló közös pontjának létezése csak azon múlik, hogy az átlók végpontjai a sokszög határán elválasztják-e egymást, illetőleg vannak e közöttük egybeesők. Elég ezért, ha a feladat állítását a szabályos n-szögre bizonyítjuk be.
A szabályos n-szög átlóit csoportokba soroljuk, egy csoportba sorolva az egymással párhuzamosakat. Ha belátjuk, hogy nincs n-nél több csoport, bebizonyítottuk a feladat állítását, hiszen akkor n-nél több átló kiválasztásakor arra kényszerülünk, hogy egy csoportból több átlót válasszunk ki, s az ilyen párhuzamos átlóknak nincs közös pontjuk.
Az említett csoportok száma valóban nem lehet n-nél nagyobb. Ha ugyanis a sokszög középpontjából merőlegest állítunk egy átlóra, ez a merőleges egyenes a sokszögből csak csúcsban vagy egy oldal felezőpontjában léphet ki, ti. aszerint, hogy a sokszög kerületének az átló végpontjait összekötő, a merőleges által felezett része páros vagy páratlan sok oldalból áll-e (2. ábra). Minthogy n csúcs és n oldalfelezőpont van, minthogy továbbá minden merőleges e 2n pont közül más-más kettőt metsz ki, csak n ilyen merőleges lehet. Mivel az egy csoportba sorolt átlók ugyanarra az egyenesre merőlegesek, a csoportok száma valóban nem lehet n-nél nagyobb.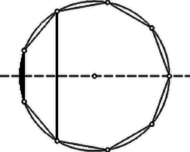
 
 
2. ábra
 

 
Megjegyzések. 1. Beláttuk, hogy a feladat előírása szerint nem választható ki n-nél több átló. Kérdés, n átló kiválasztható-e.
Nyilván nem választható ki, ha n értéke 3 vagy 4, mert a háromszögnek nincs átlója, a négyszögnek pedig csak két átlója van. Ha viszont n≥5, akkor mindig kiválasztható n átló az előírt módon, amint ezt a 3. ábra könnyen általánosítható példája bemutatja. Igaz marad ez természetesen akkor is, ha az oldalak kiválasztását is megengedjük. Ebben az esetben azonban nincs már szükség a háromszög és a négyszög kirekesztésére.
 
 
3. ábra
 

Nem választható ki viszont minden esetben n páronként közös ponttal rendelkező összekötő szakasz, ha nem egy konvex sokszög csúcsairól, hanem a sík n pontjáról van szó. Ha az egyik pontot az összes többivel összekötjük, az előírást kielégítő n-1 szakaszt kapunk. Többet nem kaphatunk pl. akkor, ha az ABCΔ csúcsairól és a háromszögben haladó BC körív n-3>0 további pontjáról van szó (4. ábra). Ezt a következőképpen láthatjuk be: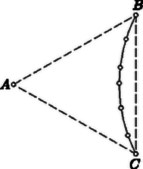
 
 
4. ábra
 

A-ból csak n-1 szakasz indul ki. A BC ív n-1 pontját összekötő szakaszok közül is csak n-1 választható ki az előírásnak megfelelően, hiszen ezek egy konvex (n-1)-szög csúcsai. Ha A-ból induló szakaszt is és a BC ív pontjait összekötő szakaszt is kiválasztunk, akkor ezek közös pontja csak az A-ból induló szakasz másik végpontja lehet. Ha tehát a kiválasztott szakaszok között csak egyetlen A-ból induló van, akkor ennek másik végpontja szükségképpen minden más kiválasztott szakasznak is végpontja, s ezért így is csak n-1 szakaszhoz juthatunk. Ha viszont két A-ból induló szakaszt és a BC ív egy húrját is kiválasztjuk, akkor ezek szükségképpen háromszöget alkotnak, és további szakasz már nem választható hozzájuk az előírás megsértése nélkül.
Megemlítjük itt még, hogy ha tetszőleges n-szög esetében csak a belső átlók közül válogathatunk, akkor még n-1 páronként közös ponttal rendelkező sem választható ki minden esetben, hanem csak 2. Az 5. ábra példája mutatja, hogy többet nem követelhetünk meg. Nem nehéz bebizonyítani, hogy ha n≥5, akkor két csatlakozó belső átló mindig található, e bizonyítást azonban az olvasóra hagyjuk.
 
 
5. ábra
 

2. Felmerül a kérdés, hogy ha a sík (hármasával nem egy egyenesen elhelyezkedő) n pontját összekötő szakaszok közül ki lehet választani n páronként közös ponttal rendelkezőt, akkor ez az n szakasz milyen ábrát alkothat. Bebizonyítjuk, hogy csak egy páratlan oldalú csillagsokszög adódhat, amelyhez még a csúcsaiból induló, az odafutó oldalak szögtartományában haladó szakaszok járulhatnak (6. ábra).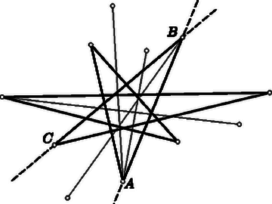
 
 
6. ábra
 

Második megoldásunk mutatja, hogy az elsőfokú pontokba futó szakaszok elhagyása után csupa másodfokú ponttal rendelkező ábrához kell jutnunk (ehhez az eredményhez I. megoldásunk alapján is eljuthatunk). Ez az ábra most nem lehet üres, mert akkor az utolsó elhagyás egyszerre két végpontot szüntetne meg, s így csak az mk<n-k egyenlőtlenség lehetne érvényes, ami kizárja d-n teljesülését. Eszerint az elhagyások után maradó ábrában zárt töröttvonal található, mert valamelyik szakaszon elindulva a pontok másodfokúsága miatt mindig folytathatjuk utunkat csatlakozó szakaszon, és így valamikor már bejárt szakaszhoz kell érnünk. Minthogy az ilyen zárt töröttvonal szakaszai vagy csatlakoznak, vagy metszik egymást, csillagsokszöghöz jutottunk. Ennek szükségképpen páratlan sok csúcsa van. Ha ugyanis AB egy szakasza, akkor a további csúcsok a szakaszok metszése miatt váltakozva az AB egyenes egyik és másik oldalán helyezkednek el, de közülük az A-val és B-vel szomszédos ugyanazon az oldalon van, hiszen az ezeket AB-vel összekötő szakaszok is metszik egymást.
Megvizsgáljuk, hogy a már megtalált csillagsokszögön kívül milyen szakaszok szerepelhetnek még az eredeti ábrában. Ha egy pont a csillagsokszög csatlakozó AB, BC oldalai által meghatározott ABC szögtartományban vagy csúcsszögének tartományában van, akkor belőle csak B-be futhat szakasz, mert különben nem volna közös pontja AB és BC mindegyikével. Ilyen szakasz is csak akkor felelhet meg, ha magában az ABC szögtartományban van, mert különben nem volna közös pontja a csillagsokszög további oldalaival, amelyek ezen a szögtartományon belül kötik össze az AB, BC szakaszokat.
Állításunk teljes bizonyításához elég már csak azt igazolnunk, hogy a sík minden pontja a csillagsokszög valamelyik szögének vagy szöge csúcsszögének tartományában helyezkedik el. Ennek igazolására az AB egyenest B körül elforgatjuk úgy, hogy az ABC szögnek és csúcsszögének tartományát végigsöpörve CB helyzetbe jusson. Ezt követően C körül forgatjuk el ugyanúgy, majd a következő csúcs körül, míg végül is eredeti helyzetébe tér vissza, tehát együttesen 180∘ egész számú többszörösével fordul el.
Nem lehetséges azonban, hogy az egyenes 180∘-nál többet forduljon el. Az ellenkező esetben ugyanis egyenesünk az első félfordulat során olyan a helyzetet is elfoglal, amelyen a csillagsokszög egyetlen csúcsa helyezkedik csak el, ti. az, amely körül éppen forgatunk. A második félfordulat során egyenesünk a-val párhuzamos b helyzetbe jut. Azonos helyzetről nem lehet szó, mert a nem tartalmaz második csúcsot. A párhuzamos a, b egyenesek mindegyike kettévágja a csillagsokszög egy-egy szögét, ezért e szögek egy-egy szára a párhuzamosok sávján kívül helyezkedik el. Így tehát az ezeket a szárakat szolgáltató sokszögoldalaknak a feltételezett esetben nem lehetne közös pontjuk.
Már csak azt kell belátnunk, hogy ha egy egyenes a síkban mozog, és 180∘-os elfordulás után eredeti helyzetébe tér vissza, akkor mozgása során a sík minden pontján áthalad. Ez valóban így van, mert ha valamely P pontnak nem volna meg ez a tulajdonsága, akkor P-ből mindig félegyenest indíthatunk, amely a mozgó egyenest merőlegesen metszi. Ez a félegyenes P körül forog, és a 180∘-os elfordulás után ellentétes irányú lesz. Nem metszheti ezért merőlegesen ugyanazt az egyenest, amelyet a mozgás kezdetekor metszett.
3. Felvetjük azt a kérdést is, hogy hányat kell kiválasztani egy konvex n-szög átlói közül, hogy bizonyosan legyen ezek között k olyan, amelyeknek páronként nincs közös pontja. Feladatunk a k=1 esettel foglalkozott. Ebben az esetben n+1 átló kiválasztása megfelel, de kevesebb nem.
Könnyű belátni, hogy a felvetett általános esetben kn+1 átló kiválasztása megfelel, sőt megfelel akkor is, ha nemcsak az átlók, hanem az oldalak közül is válogathatunk. Ez harmadik megoldásunkból szinte közvetlenül kiolvasható, mert ha kn+1 átlót vagy oldalt választunk ki az n csoportból, akkor valamelyikből legalább (k+1)-et kell kiválasztanunk.
Nehezebb megmutatni, hogy kisebb szám nem felel meg. Megmutatjuk, hogy ez valóban így van, vagyis olyan előírást adunk a konvex n-szög átlói közül nk átló meghúzására, hogy ne lehessen ezek közül k+1 páronként közös pont nélküli átlót kiválasztani.
Csak akkor van értelme ilyen előírás megadásának, ha az n-szögnek egyáltalában van k+1 páronként közös pont nélküli átlója. Ez csak akkor igaz, ha n≥2k+4. Ha ugyanis olyan átlókat tekintünk, amelyeknek nincs közös pontjuk, akkor bármelyiknek bármelyik oldalán vagy található olyan csúcs, amely nem végpontja átlóink egyikének sem, vagy pedig van ezen az oldalon további átló. Ez utóbbi esetben tovább haladhatunk, és esetleg újabb meg újabb átlóhoz jutunk, de végül is el kell jutnunk olyan csúcshoz, amely átlóinknak nem végpontja. Ilyen csúcs ezek szerint legalább kettő van, ti. egy átló mindkét oldalán legalább egy. Ha tehát k+1 átlóról van szó, akkor ezek 2(k+1) végpontján kívül még legalább két csúcsnak kell lennie.
Legyen tehát n≥2k+4, és legyenek az n-szög csúcsai sorban
A0,A1,B1,A2,B2,...,Ak,Bk,Ak+1,Ak+2,C1,C2,...,Cn-2k-3.
Rajzoljuk meg ebben a konvex n-szögben mindazokat az átlókat, amelyeknek legalább az egyik végpontja B jelű, továbbá A0Ak+2 kivételével mindazokat az átlókat, amelyek két A jelű csúcsot kötnek össze (7. ábra; a 3. ábra a k=1 esetben ugyanezt mutatja be). Könnyű ellenőrizni, hogy összesen nk átlót rajzoltunk meg.
 
 
7. ábra
 

Állítjuk, hogy ezek közül az átlók közül csak k darab páronként közös pont nélküli választható ki. Ezt k-ra vonatkozó teljes indukcióval bizonyítjuk be. Már tudjuk, hogy állításunk a k=1 esetben helyes. Legyen tehát k>1, és tegyük fel, hogy állításunk minden olyan esetben helyes, amikor k szerepét k-nál kisebb szám tölti be.
Ha valamennyi kiválasztott átlónak van B jelű csúcsa is, akkor számuk nem lehet k-nál nagyobb, hiszen csak k darab B jelű csúcs van. Elég ezért azzal az esettel foglalkoznunk, amikor olyan h átlót is kiválasztunk, amely két A jelű csúcsot köt össze. Megvizsgáljuk, hogy h két oldalán hány további átló választható ki. Vágjuk fel tehát n-szögünket két sokszögre, S1-re és S2-re. S1 csúcsai csak A és B jelűek, S2 csúcsai között pedig a C jelűek is szerepelnek. Helyezkedjék el a B jelű csúcsok közül j darab S1 határán, k-j pedig S2 határán. Nyilván j>0, viszont k-j=0 is lehetséges.
Azt állítjuk, hogy S1-ben csak j-1 olyan átló választható ki, amelyeknek egymással és h-val nincs közös pontjuk. Már beláttuk, hogy j darab páronként közös pont nélküli átló csak legalább 2j+2 oldalú sokszögben van. S1 legfeljebb éppen ennyi oldalú lehet (ha ti. A0 vagy Ak+2 is szerepel h végpontjai között), azonban olyan átlók számát vizsgáljuk, amelyeknek h-val sincs közös pontjuk. Az ilyen átlók pedig annak az S'1 sokszögnek is átlói, amelyet S1-ből kapunk, ha egy átlójával a h oldalt és egy szomszédos oldalát levágjuk (8. ábra). Minthogy S'1 legfeljebb 2j+1 oldalú, S1-ből sem lehet az előírt módon j-1 átlónál többet kiválasztani.
S2-ben csak akkor van egyáltalában átló a megrajzoltak közül, ha j<k, azaz van S2-nek B jelű csúcsa is. Feltesszük tehát, hogy j<k. Vizsgáljuk meg, hogy S2 határán a csúcsok betűjelzése olyan elrendezésű-e, mint n-szögünkben, természetesen k helyett csak k-j darab B jelű csúccsal. Ez bekövetkezik, ha h végpontjai között A0 vagy Ak+2 is szerepel. Minden más esetben ugyancsak elérhetjük ezt azáltal, hogy S2-bő1 egy átlóval a h oldalt és egy csatlakozó, B jelű pontba vezető oldalt levágunk (8. ábra). A kiválasztható átlók számát vizsgálva az így kapott S'2 sokszögre térhetünk át, hiszen csak olyan átló választható ki, amelynek h-val sincs közös pontja. Minden esetben alkalmazhatjuk tehát az indukciós feltevést, s ezért kimondhatjuk, hogy S2-ből a követelményt kielégítő módon nem lehet k-j átlónál többet kiválasztani.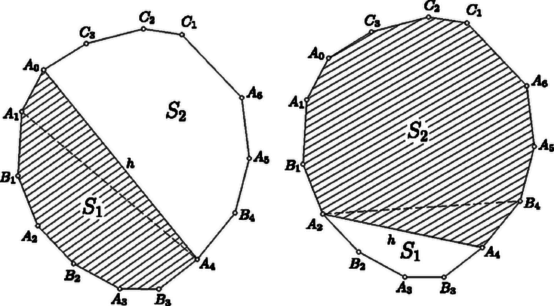
 
 
8. ábra
 

Ezek szerint az általunk megrajzolt nk átló közül kiválasztható, páronként közös pont nélküli átlók száma (magára h-ra is gondolva) valóban legfeljebb 1+(j-1)+(k-j)=k.
Megoldatlan kérdés, hogy ha a most tárgyalt problémát nem egy konvex n-szögre, hanem a sík n pontjára vetjük fel, vajon szintén nk+1 adja-e a feleletet.
4. Feladatunk problémájának utolsó általánosításaként még az angol Conway sejtését említjük meg. E sejtés szerint, ha a sík n pontját összekötő vonalakat rajzolunk, amelyek közül bármely kettőnek vagy van közös végpontja, vagy pedig egyetlen pontban metszik egymást, de más közös pontjuk nincs, akkor ezeknek az összekötő vonalaknak a száma csak legfeljebb n lehet. Hangsúlyozzuk, hogy vonalak érintkezési pontja nem metszéspont, a vonalak érintkezését kizártuk.
Eldöntetlen kérdés, hogy vajon ez a sejtés helyes-e. Említést érdemel, hogy a vizsgált ábrák itt lényegesen mások, mint az összekötő szakaszokra felvetett problémánál, és nem csak a vonalak görbülése miatt. Ezt a 9. ábra is mutatja, melyben 6 pontot 6 vonal köt össze az előírásnak megfelelően, mégpedig ciklikus módon. Láttuk, hogy szakaszok esetében ez csak páratlan sok pontra lehetséges.
 
 
9. ábra
 

Olvasóink is megkísérelhetik a vonalakra vonatkozó probléma megoldását. Ha valakinek sikerül az előírásnak megfelelően úgy rajzolnia vonalakat, hogy számuk nagyobb, mint végpontjaik együttes száma, akkor megoldotta a problémát. Nehezebb a probléma lezárása, ha nemcsak nem sikerül ilyen ábrát rajzolni, hanem ilyen ábra nincs is. Ebben az esetben ennek bebizonyítására volna szükség.
 
Harmadik feladat. Az ABCD gúla tartalmazza (belsejében vagy határán) a D-től különböző P pontot. Bizonyítsuk be, hogy a PA, PB, PC távolságok között van olyan, amely kisebb a DA, DB, DC távolságok valamelyikénél.
 
I. megoldás. Feltehetjük, hogy P nincs a DA, DB, DC oldaléleken, mert ha pl. a DA élnek D-től különböző pontja, akkor PA<DA.
Elég megmutatnunk, hogy az APD, BPD, CPD háromszögek valamelyike P-nél derékszögű vagy tompaszögű. Ha ugyanis pl. az APDΔ ilyen, akkor DA a legnagyobb oldala, s ezért 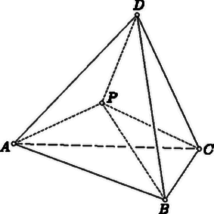PA<DA (10. ábra).
 
 
10. ábra
 

P-ből induló, PD-vel hegyesszöget bezáró félegyenesek annak a féltérnek a belsejében haladnak, amelyet a P-ben PD-re merőlegesen állított sík határol, s amely tartalmazza a D pontot. Ha tehát az előbb említett háromszögek P-nél mindannyian hegyesszögűek, akkor a gúla minden csúcsa a mondott féltér belsejében van, tehát maga a gúla is, s ez ellentmond annak, hogy P a féltér határsíkján helyezkedik el. Ez az ellentmondás bizonyítja, hogy háromszögeink között valóban van olyan, amely P-nél nem hegyesszögű.
 
 
11. ábra
 

II. megoldás. A P ponton át az ABC síkra merőlegest állítunk. Legyen Q ennek a merőlegesnek az ABC síktól legtávolabbi, még a gúlához tartozó pontja (11. ábra). Q tehát az ABD, ACD, BCD oldallapokon helyezkedik el, legyen pl. az ABD lapon. Állítsunk ennek síkjában a Q ponton át merőlegest az AB egyenesre. Legyen R ennek a merőlegesnek az AB egyenestől legtávolabbi, még az ABD háromszöghöz tartozó pontja. R tehát az AD, BD oldaléleken helyezkedik el, legyen pl. az AD szakasznak pontja.
Ha egy pontot merőlegesen távolítunk egy síktól vagy egy egyenestől, akkor a sík minden pontjától, illetőleg az egyenes minden pontjától távolodik. Ezért
PA≤QA≤RA≤DA.
Mindenütt meg kellett engednünk az egyenlőséget is, hiszen P=Q, Q=R, R=D mindegyike lehetséges. Mindezek azonban egyszerre nem teljesülhetnek, mert P nem azonos D-vel. Ezért legalább egy helyen az egyenlőtlenség jele érvényes, és így PA<DA.
III. megoldás. A PD szakaszt merőlegesen felező sík kettévágja gúlánkat, hiszen P és D a sík más-más oldalán van, és a gúlához tartozik. Ebből következik, hogy e sík által határolt félterek mindegyikének a belsejében van csúcsa a gúlának, mert ha az egyikben nincs, akkor a csúcsaival együtt az egész gúla is a másik féltérben van, s így a sík nem vághatná ketté a gúlát. Ha pl. az A csúcs a P pontot tartalmazó féltér belsejében van, akkor PA<DA, hiszen e féltér belső pontjai közelebb vannak P-hez, mint D-hez.
 
Megjegyzések. 1. Mindhárom megoldásunk a feladat állításán túlmenően azt is bebizonyítja, hogy a PA, PB, PC távolságok között van olyan, amely kisebb, mint a DA, DB, DC távolságok közül a vele azonos végpontú.
2. A második megoldás változtatás nélkül alkalmazható akkor is, ha nem három, hanem akárhány oldalú gúláról van szó. Bizonyítja tehát, hogy egy gúlának a csúcsától különböző (belsejében vagy határán elhelyezkedő) pontja közelebb van az alaplap valamelyik szögpontjához, mint a gúla csúcsa.
3. A harmadik megoldás alapján még többet is kimondhatunk. Módosítás nélkül helyes marad ez a megoldás akkor is, ha benne gúla helyett tetszőleges poliéder szerepel. Bebizonyítja tehát, hogy egy poliéder valamely D csúcsától különböző (belsejében vagy határán elhelyezkedő) pont közelebb van a poliéder valamelyik D-től különböző csúcsához, mint D. Ugyanez az első bizonyítás módszerével is könnyen bizonyítható.
4. Legyenek a háromoldalú gúla oldalélei d1≤d2≤d3, egy a gúla csúcsától különböző pontjának az alapháromszög csúcsaitól mért távolságai pedig p1≤p2≤p3. Az indexezés itt csak a nagyságrendtől függ, és nem jelenti, hogy az azonos indexűeket azonos végpontú szakaszok adják. Kérdezhetjük, hogy ha megadunk valamilyen d1, d2, d3, p1, p2, p3 távolságokat, vajon található-e olyan gúla s abban olyan pont, amelyekhez éppen a megadott értékek tartoznak.
Feladatunk kimondja, hogy
p1<d3
szükséges ahhoz, hogy ez lehetséges legyen. A második megoldásból könnyen kiolvasható, hogy
p1+p2<d2+d3
is szükséges feltétel, hiszen ott PA+PB≤QA+QB≤DA+DB, és az egyenlőség nem teljesülhet mind a két esetben.
Érdemes megemlíteni, hogy pl. p2<d3 már nem kell, hogy teljesüljön, és nem kell teljesülnie a p1+p2+p3<d1+d2+d3 egyenlőtlenségnek sem. Mindez kiolvasható a 12. ábrából, amelyen a szakaszok mellett azok hossza áll. Ezek a tapasztalatok további szükséges feltételek keresésekor óvatosságra intenek.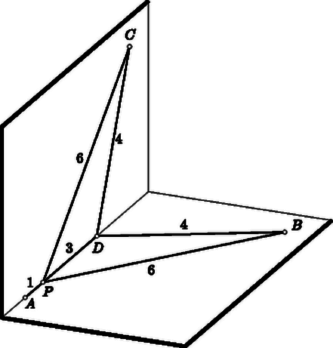
 
 
12. ábra
 

Vannak azonban még további szükséges feltételek is, mert ha a már említettek mind teljesülnek, ez még nem elégséges ahhoz, hogy valóban található legyen a d1, d2, d3, p1, p2, p3 értékeket szolgáltató gúla és pont. Ilyen egyszerű formájú szükséges és elégséges feltétel nem ismeretes. Megkeresése talán érdekes, de nagyon könnyűnek nem látszó feladat.
 
 Hajós György