Cím: Az 1962. évi Arany Dániel tanulóversenyek II. fordulóján kitűzött feladatok megoldása: Kezdők (I. osztályosok) versenye
Szerző(k):  Fried Ervin ,  Surányi János 
Füzet: 1963/február, 49 - 52. oldal  PDF  |  MathML 
Témakör(ök): Arany Dániel

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

1. feladat. Egy ember az A HÉV-megállónál várakozik. Elunja a várakozást és elindul a következő B HÉV-megálló felé. Mikor az A és B közötti út 1/3-át megtette, megpillantja az A megálló felé 30km/óra sebességgel közeledő szerelvényt. Ha teljes sebességgel futni kezd akár az A, akár a B megálló felé, éppen eléri a vonatot. Mekkora az a maximális sebesség, amellyel futni tud?

 

I. megoldás. Legyen a keresett sebesség v km/óra, az AB útszakasz hossza x km, és jelölje C azt a pontot, amelyből az ember megpillantja a vonatot.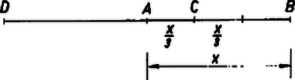
 
 
1. ábra


Ekkor CA=x/3, CB=2x/3, és az ezen utak megtételéhez szükséges idők x/3v óra, ill. 2x/3v óra. Ugyanennyi idő alatt ér a vonat is a megpillantáskor volt helyzetéből A-ba, B-be, ezért a vonatnak az AB út megtételéhez szükséges ideje e két idő különbsége: x/3v óra. Ez az idő a vonat sebességével kifejezve x/30, így a két kifejezés egyenlőségéből v=10. Emberünk maximálisan 10 km/óra sebességgel tud futni.
 
II. megoldás. A feladat egyenlet nélkül is megoldható. Mire az ember C-ből eljut A-ba, addigra a vonat is A-ba ér. Így ha az ember B felé fut, az alatt az idő alatt, amíg a vonat A-ba ér, ő ugyanakkora távolságot tesz meg, mint amennyire C az A-tól van, vagyis az AB út harmadát. Ezért B-ig már az út 2/3 részét megtette, csak az 1/3 rész van hátra. Mialatt ezt a harmadot megteszi, a vonat A-ból B-be jut, vagyis megteszi az egész AB távolságot. Így az ember sebessége a vonat sebességének harmadrésze, azaz 10 km/óra.
 

Megjegyzések. 1. A megoldásból nem adódik ki a tekintetbe vett útszakaszok hossza. A közölt egyetlen összefüggés csak a keresett ismeretlen meghatározására elegendő.
2. Az viszont kiderül a feladat feltételeiből ‐ és ez is felhasználható a megoldáshoz ‐, hogy a vonat a megpillantáskor (az ábrán D) annyira van A-tól, mint A van B-től, hiszen az utas B-ig futva kétannyi utat tesz meg, mint ha A-ba fut, így a vonat B-ig, ill. A-ig megtett útjai közt is ez az arány.
 

2. feladat. Írjuk fel egy szám jegyeit fordított sorrendbe. Mutassuk ki, hogy az így kapott (tízes számrendszerbeli) szám nem lehet az eredeti szám kétszerese.
I. megoldás. Legyen az eredeti N szám első (legmagasabb helyértékű) jegye a, utolsó jegye b, vagyis N=a...b¯, és tegyük fel az állítással ellentétben, hogy kétszerese egyenlő a jegyek fordított sorrendű felírása útján adódó számmal: 2N=b...a¯. Mivel 2N páros szám, azért utolsó jegye, a is páros. Másrészt 2N ugyanannyi jegyű, mint N, ezért a kisebb 5-nél, így a csak 2 vagy 4 lehet.
Azonban mindkét kiindulás lehetetlenségre vezet. Ha a=2, akkor 2N első jegye 4 vagy 5, az a utáni számjegy 2-vel való szorzásakor esetleg fellépő, átviendő maradék szerint. Így viszont 2N vagy 8-asra, vagy 0-ra végződik, tehát nem 2-re. Hasonlóan a=4-ből b=8, vagy 9, és így 2N utolsó jegye 6 vagy 8, nem pedig 4. ‐ Nem lehetséges tehát, hogy egy szám jegyeit fordított sorrendben leírva a szám kétszeresét kapjuk.
II. megoldás. Célhoz juthatunk párossági meggondolások nélkül is. Láttuk, hogy b=2a+1, vagy b=2a attól függően, hogy a 2-vel való szorzás utolsó előtti lépésében lépett-e fel maradék vagy nem. (b=2a+2 már lehetetlen számjegy, mert az ezzel kezdődő számokat 2-vel osztva a hányados (a+1)-es jeggyel kezdődik, nem a-val.) A szorzás első lépésében is két eset lehetséges aszerint, hogy 2b eléri, esetleg meg is haladja a 10-et, vagy nem. Miután mindig 2b<20, az utóbbi esetben 2b=a, az előbbiben 2b=a+10. b előbbi kifejezéseit ide behelyettesítve a-ra egyismeretlenes egyenleteket kapunk:
4a+2=a,4a+2=a+10,4a=a,4a=a+10.
Ezekből 3a értéke vagy -2, vagy 0, vagy 8 vagy 10. Így számjegy gyanánt használható ‐ ti. 0 és 9 közti egész ‐ a-érték csak a 0, de N első jegye gyanánt ez sem fogadható el. Ezek szerint valóban nincs a szóban forgó tulajdonsággal bíró szám.
 

3. feladat. Bizonyítsuk be, hogy bármely konvex négyszögben van olyan oldal, amely kisebb a hosszabbik átlónál.
 

I. megoldás. Jelöljük egy ABCD konvex négyszög átlóinak metszéspontját M-mel (2. ábra). Alkalmazzuk a háromszög-egyenlőtlenséget az ABM, BCM, CDM, DAM háromszögekre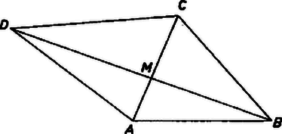
AB<AM+BM,BC<BM+CM,CD<CM+DM,DA<DM+AM.
A négy egyenlőtlenséget összeadva
AB+BC+CD+DA<2(AM+BM+CM+DM)=2(AC+BD).
A bal oldal nem kisebb a legkisebb oldal 4-szeresénél, a jobb nem nagyobb a nagyobb átló négyszeresénél, s így valóban a legkisebb oldal kisebb a nagyobbik átlónál.
 
 
2. ábra
 

II. megoldás. Vizsgáljuk pl. a négyszög AB oldalát és AC átlóját. Ha AB<AC, akkor a feladat állítása érvényes: a legkisebb oldal biztosan kisebb a nagyobbik átlónál.
Ha AB≥AC, akkor megmutatjuk, hogy az AB-vel szemben levő oldal kisebb a másik átlónál: CD<BD. A feltételből ugyanis következik (az ABC háromszögre alkalmazva az oldalak és szögek közti összefüggést), hogy
ACB∢≥ABC∢.
Másrészt konvex négyszög átlói két részre osztják a négyszögnek a végpontjaikban levő szögeit, így
DCB∢>ACB∢≥ABC∢>DBC∢.
Ebből ismét az oldalak és szögek közti összefüggés alapján nyerjük, hogy BD>CD, amint állítottuk. Ezzel a bizonyítást befejeztük.
 

Megjegyzések. 1. A feladat állításánál többet is bizonyítottunk: konvex négyszög bármelyik szemben fekvő oldalpárjának egyik tagja kisebb valamelyik átlónál (tehát a hosszabb átlónál minden esetre kisebb), s így legalább két oldal kisebb, mint az átlók hosszabbika. Azt is látjuk, hogy ha csak két ilyen oldal van, ezek szomszédosak.
2. A megoldásból az is következik, hogy ha valamelyik oldal nem kisebb egyik átlónál sem, akkor a szemben fekvő oldal mindkét átlónál kisebb.
3. A rövidebb átlóra a bizonyítás azt adja, hogy ahány oldal nem kisebb a rövidebb átlónál, legalább annyi a hosszabbik átlónál kisebb oldal van.
 

III. megoldás. Legyen a négyszög legnagyobb szöge az ADC szög (3. ábra). Ez legalább 90∘, különben ugyanis a szögek összege nem lehetne 360∘. Így az ADC szög nagyobb az ADC háromszög másik két szögénél. Ezért az ADC szöget bezáró DA és DC oldalak ‐ egyszersmind a négyszögnek is oldalai ‐ kisebbek a háromszög AC oldalánál, ami a négyszögnek átlója. Ezzel az állítást bebizonyítottuk.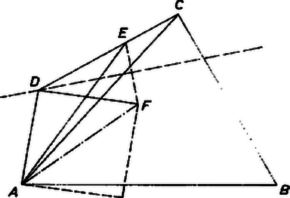
 
 
3. ábra
 

Megjegyzések. 1. A mondottakból következik, hogy ha egy konvex négyszögben két szemben levő szög egyike sem hegyesszög, akkor mind a négy oldal kisebb a hosszabb átlónál.
2. Megmutatjuk, hogy minden konvex négyszögnek a legkisebb oldala fölé négyzetet rajzolva még ennek az átlója sem nagyobb a hosszabb átlónál.
Legyen továbbra is ADC∢≥90∘, válasszuk a betűzést úgy, hogy álljon DC≥DA, mérjük rá a DA szakaszt D-től a DC félegyenesre, és legyen a végpont E. Ekkor AE≤AC, mert az ADE háromszögből, amennyiben E különbözik C-től,
AEC∢=ADE∢+DAE∢>ADE∢≥90∘,
tehát az AEC háromszögben E-nél tompaszög van, AC>AE. Ha ADE∢=90∘, akkor AE az említett négyzet-átló, s így állításunk helyes. Ha ADE∢>90∘, akkor állítsunk merőlegest D-ben AD-re és mérjük fel erre a DF=DA szakaszt, azon az oldalon, amelyen a négyszög fekszik. Így DF=DE, tehát D rajta van az EF szakasz felező merőlegesén. A pedig e merőlegesnek F-et tartalmazó partján van, mert a felező merőlegesből D körüli, hegyessszögű forgással jutunk DF-be (ti. akkorával mint DE-be), onnan tovább 90∘-os forgással DA-ba, és a két forgás összege kisebb 180∘-nál. Ez esetben AF, a kérdéses négyzetátló, kisebb AE-nél. Ha pedig E egybeesik C-vel, akkor AF≤AE=AC. Ezzel igazoltuk állításunkat.
Pythagorász tételéből tudjuk, hogy az AD oldalú négyzet átlójának hossza AD2. Eszerint konvex négyszög két, tompaszöget vagy derékszöget bezáró oldala közül a kisebbik 2-szöröse kisebb valamelyik átlónál vagy egyenlő vele. 1
 

IV. megoldás. Az átlók M metszéspontja mindegyik átlót két részre osztja (2. ábra). Válasszuk a betűzést úgy, hogy DM a négy szakasz legnagyobbika legyen, vagy a legnagyobbak egyike. Ekkor
AB<AM+BM≤DM+BM=BD,
tehát van olyan oldal, amelyik kisebb egy átlónál, s így a legkisebb oldal bizonyosan kisebb a nagyobbik átlónál.
 

Megjegyzések. 1. A választott jelölések mellett fennáll
BC<BM+CM≤BM+DM=BD
is, tehát konvex négyszögnek mindig van két szomszédos oldala, amelyek rövidebbek a közös végpontjukból induló átlónál.
2. Kiindulhatunk a legkisebb átlórészből is. Ha pl. AM nem nagyobb a BM, CM, DM szakaszok egyikénél sem, akkor
AB<AM+BM≤BM+DM=BD
és
AD<AM+DM≤BM+DM=BD.
Így azt kaptuk, hogy konvex négyszögben mindig van két szomszédos oldal, amelyek kisebbek a velük háromszöget alkotó átlónál.
A két oldalpár közös végpontjai csak akkor lehetnek szemközti csúcsok, ha ugyanaz a szakasz szerepel a legrövidebbek közt és a leghosszabbak közt is, vagyis ha M a két átlót csupa egyenlő részekre osztja (téglalap esetén). Ekkor bármelyik szomszédos oldalpár rendelkezik mindkét tulajdonsággal. Egyébként vagy mindkét állítás ugyanarról az oldalpárról szól, vagy ugyanarról az átlóról (és a szóban forgó két oldal közül egy oldal kétszer nyer említést).
A két állításból így az is következik, hogy egy konvex négyszögnek vagy van két szomszédos oldala, amelyek mindegyike kisebb mindkét átlónál, vagy három oldala kisebb a hosszabb átlónál.
 
 Fried Ervin, Surányi János
1Lásd az 1961. évi Kürschák József matematikai tanulóverseny 1. feladatát, K. M. L. 24 (1962) 98. o.