Cím: Sylvester egy tételéről és Erdős egy sejtéséről
Szerző(k):  Kárteszi Ferenc 
Füzet: 1963/január, 3 - 9. oldal  PDF  |  MathML 
Témakör(ök): Szakmai cikkek

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

1. E folyóirat XXIV. kötetének 5. számában Erdős Pál egy gazdag tartalmú cikkben ,,Néhány elemi geometriai problémáról'' címen meggyőzte az olvasókat arról, hogy a matematika fejlődése során sok olyan probléma merül fel, mely nem kíván nagy matematikai felkészültséget, s mégis nehéz, mert a megoldásra alkalmas módszereket kell előbb még megteremteni. Ebben a közleményben a mondott Erdős-cikkben szereplő két kérdés kapcsán azt kívánom megmutatni, miként vezet a problémán való elmélkedés a megfelelő módszerek kialakításához.
Először ismert tétel elemi bizonyításához keresünk módszert. Legyen adva a síkon 9 pont: P1,P2,...,P9. Ezek kettenként legfeljebb

129⋅(9-1)=36
(összekötő-) egyenest feszítenek ki. A 9 pont által így kifeszített egyenesek száma lehet 36-nál kisebb is, hogyha az összekötő egyenes a 9 közül 2-nél több ponton is átmegy. Ha például egy kifeszített egyenes a 9 pont közül éppen 3 pontot tartalmaz (sem többet, sem kevesebbet), akkor a pontkilenceshez tartozó 3-pontú egyenesnek fogjuk nevezni. Fölmerül a következő kérdés: 9 pont esetén maximálisan hány 3-pontú egyenes fordulhat elő ?
A legtöbb emberben először az a sejtés támad, hogy a kérdéses maximum 8. Ugyanis az 1. ábrára gondol.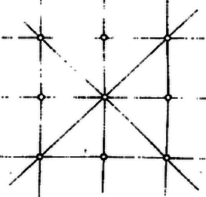
 
 
1. ábra
 

Aki azonban ismeri az ún. Pappos ‐ Pascal tételt, könnyen megcáfolja ezt az első sejtést egy ,,jobb ellenpéldával''.
A mondott tétel szerint tudjuk a következőket. Két tetszőleges egyenesen három-három tetszőleges pontot választunk (az a és b egyenesen az 1, 3, 5 és 2, 4, 6 pontokat). Ezeket a számozás rendjében ciklikusan összekötjük, vagyis megrajzoljuk az 12, 23, 34, 45, 56, 61 egyeneseket. Azután párokba osztjuk e hat egyenest: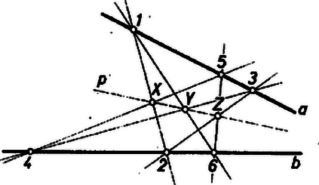
  12 23 34  45 56 61  
a párokat az oszlopok két-két eleme alkotja. Ezek a párok rendre az X, Z, Y metszéspontokat szolgáltatják. A szóban forgó tétel azt mondja, hogy az így származtatott X, Y, Z pontok egy egyenesbe esnek; a 2. ábrán a p egyenesről van szó.
 
 
2. ábra
 

Ez az ábra az ellenpélda, hiszen itt a 9 ponthoz 9 hárompontú egyenes tartozik. Nyomban fölmerül az ötlet, hogy az elemek szerencsésebb elhelyezésével még a 2, 5, Y pontok is egy egyenesbe eshetnek. A 3. ábrán éppen ilyen alakzatot mutatunk be. Tehát létezik olyan pontkilences, mely 10 hárompontú egyenest feszít ki. Ebből az az újabb sejtésünk támad, hogy a keresett minimum 10. Ezt persze nem bizonyítja az a tény, hogy a legötletesebb próbálkozásokkal sem tudunk 9 pontot úgy elhelyezni, hogy legalább 11 hárompontú egyenest feszítsenek ki. Próbáljuk hát meg bebizonyítani, hogy ilyen elhelyezés nincs. Ez az eddigiektől eltérő jellegű és nehezebb feladat.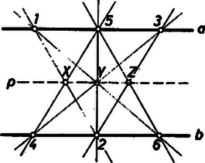
 
 
3. ábra
 

2. Megmutatjuk, hogy a ,,létezik a síkon 9 pont, mely legalább 11 hárompontú egyenest feszít ki'' feltevésből képtelen következmények adódnak. A kissé hosszadalmas és szokatlan jellegű okoskodások előtt még néhány ‐ pillanatnyilag hasznos ‐ fogalmat vezetünk be. Adott n pont, P1,P2,...,Pn feszítsen ki hárompontú egyeneseket is, s jelölje ezeket g1,g2,...,gm. Az így értelmezett {P1,...,Pn;g1,...,gm} alakzat bizonyos számú illeszkedést létesít. Egy illeszkedés azt jelenti, hogy egy Pr pont rajta van egy gs egyenesen (más szóval a gs egyenes átmegy a Pr ponton). Annyi illeszkedést létesít ez az alakzat, ahány ilyen helyzetviszonyú pont-egyenes-pár van benne. (Például az 1. ábra 24 illeszkedést valósít meg.)
A P pontokat a hozzájuk illeszkedő g egyenesek száma szerint osztályozhatjuk. Hogyha egy P ponthoz pontosan k számú g egyenes illeszkedik, akkor ezt a pontot k-egyenesű pontnak mondjuk. (Így például a 3. ábrán vannak négyegyenesű pontok, mégpedig a 2, 5, Y; a többiek háromegyenesű pontok. Noha az 1, 4 pontpár is kifeszít egyenest, de az nem hárompontú, s azért pl. az 1 pont jellemzésénél nem vesszük tekintetbe. Éppen úgy a 3-nál több pontú egyenest sem vesszük tekintetbe.)
No mármost tegyük fel, hogy létezik egy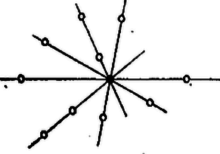
{P1,...,P9;g1,...,gm}(m≥11)
alakzat, s állapítsuk meg az általa megvalósított illeszkedések számát.
 
 
4. ábra
 

Minthogy a hárompontú egyenesek száma m, az illeszkedések száma 3m(≥33).
Ha pontonként haladva is megszámláljuk az illeszkedéseket, ugyanaz a számosság adódik. Jelölje evégből a k-egyenesű P pontok számát xk; világos, hogy e pontokhoz k⋅xk számú illeszkedés tartozik. Az is nyilvánvaló, hogy k>4 nem lehet, hiszen amint a 4. ábra is mutatja, már egy ötegyenesű pont létezése is megkívánja, hogy legalább 11 pontból álljon az alakzat. Így hát
x0+x1+x2+x3+x4=9,
és az illeszkedések száma
0⋅x0+1⋅x1+2⋅x2+3⋅x3+4⋅x4.

A kétféle megszámlálás egybevetéséből és a P pontok számából adódnak a
0⋅x0+1⋅x1+2⋅x2+3⋅x3+4⋅x4≥333⋅x0+3⋅x1+3⋅x2+3⋅x3+3⋅x4=27
összefüggések, ezek különbségéből pedig
x4-(3⋅x0+2⋅x1+1⋅x2)≥6
következik. Minthogy az x számok mindannyian nem-negatív egészek, az utolsó kifejezésből
x4≥6.
A kérdéses alakzatnak tehát legalább 6 négyegyenesű P pontja van.
A 9 pontú alakzat tanulmányozásánál a négyegyenesű pontok tulajdonságai lényeges szerepet játszanak, azért itt külön kiemelve említjük a következőket (az 5. ábrán a P 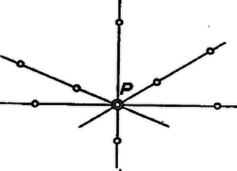pont).
 
 
5. ábra
 

α) A négyegyenesű ponton átmenő g egyenesek a szóban forgó alakzat összes pontjait felfűzik.
β) A négyegyenesű pontot az alakzat bármelyik pontjával összekötő egyenes még egy és csakis egy további pontot is felfűz.
Az x4≥6, valamint az 5. ábra segítségével könnyen belátható, hogy az alakzat négyegyenesű pontjai közül okvetlenül kiválasztható olyan három,
γ) amelyek egy egyenesbe esnek,
valamint olyan három is,
δ) amelyek nem esnek egy egyenesbe.
Ragadjuk ki a {P1,...,Pg;g1,...,gm} alakzat γ-nak megfelelő 3 pontját és egy további négyegyenesű pontot, amelyik nem lehet az előbbi hárommal egy egyenesen. Jelöljük az utóbbi pontot P1-gyel, az előbbi hármat P2, P3, P4-gyel, és vizsgáljuk egyelőre a P1P2P3 ponthármast (6. ábra). Ennek a g1, g2, g3 oldalegyeneseihez ‐ β szerint ‐ az alakzat egy-egy további pontja illeszkedik, az ábrán a P4-en kívül a P5, P6 pontok. Az alakzat további három pontja, a P7P8P9 ponthármas már nem illeszkedik a mondott oldalegyenesek egyikéhez sem.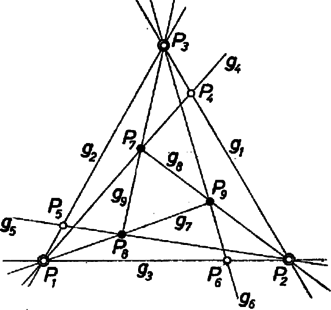
 
 
6. ábra
 

Minthogy a P1 pont négyegyenesű és a g2, g3 oldalegyenesekhez illeszkedik, még két további egyenes megy át rajta; jelölje ezeket g4 és g7. A g2 és g3 által még fel nem fűzött P1P7P8P9 pontnégyest ‐ α szerint ‐ a g4 és g7 pontpáronként felfűzi. Hasonló meggondolás alkalmazható a P2 és a P3 csúcsra is.
Ilyen módon ‐ az ábra esetlegességeitől el kell tekintenünk, abból csak arra támaszkodhatunk, amit eddig bebizonyítottunk ‐ a következő szerkezeti tulajdonságokat igazoltuk: 1. A feltüntetett pontok kimerítik az alakzat összes pontjait, s tudjuk, hogy a P1, P2, P3 és P4 pontok négyegyenesűek. 2. A feltüntetett 9 egyenes az alakzat 9 hárompontú egyenese. (Az alakzat további egyeneseiről még semmit sem tudunk, tehát még kiderülhet ‐ az ábra ellenére is ‐, hogy pl. P4, P5, P6 egy egyenesbe esnek.) 3. A P7P8P9 háromszög a P1P2P3 háromszög köré van írva, abban az értelemben, hogy az utóbbi csúcsai az előbbinek egy-egy oldalegyenesén vannak. 4. A P7, P8, P9 pontokat rendre a P1, P2, P3 csúcsokból a szemközti oldalegyenesekre vetítve a P4, P5, P6 pontot szolgáltatják.
Eddig nem vettük figyelembe azt, hogy P4 is négyegyenesű pont. Ebből és a 6. ábra igazolt tulajdonságaiból következik, hogy
g10=P4P8ésg11=P4P9
egyenesek az eddigiektől és egymástól is különböző, hárompontú egyenesek. A harmadik pontjukat megállapítandó, csak a g1, g4, g10, g11 által eddig még fel nem fűzött pontokról lehet szó, vagyis a P5 és P6 pontról. A g11 nem mehet át a P6 ponton, mert különben két pontban, a P6 és P9 pontban metszené a g6 egyenest, ami képtelenség. A harmadik pontja tehát P5. Ugyanígy adódik, hogy a g10 egyenes harmadik pontja a P6 pont. Így azonban a g10 és g11 egyenes miatt a P8 és P9 is négyegyenesű pontoknak bizonyultak.
Most a Pappos ‐ Pascal tétel alkalmazásával találhatunk egy tizenkettedik hárompontú egyenest. A 2. ábra a és b egyenesének szerepében tekintsük a 6. ábra g1 és g7 egyenesét, valamint az 123456 ponthatos szerepében a P3P8P2P1P4P9 ponthatost, akkor az X, Z, Y szerepét most itt a P7, P5, P6 veszi át. A Pappos ‐ Pascal tétel szerint tehát egy újabb hárompontú egyenes is fellép, a P7P5P6-ot felfűző g12 egyenes; ez a 2. ábra p egyenesének a szerepét veszi át. A g12 egyenes beiktatásával a P7, P5, P6 pontok is négyegyenesű pontoknak bizonyultak.
Tehát a feltevés arra vezetett, hogy az alakzat 12 egyenesből és 9 négyegyenesű pontból áll. Könnyen ellenőrizhetjük, hogy ilyen módon a 9 pont bármely kettőjét összekötő egyenesnek egy harmadik kijelölt ponton is át kellene mennie. Ez azonban az Erdős cikke elején bizonyított Gallai tétel szerint lehetetlen, mert mindig kell lennie kétpontú egyenesnek.
Feltevésünk tehát ellentmondásra vezetett. Így leszögezhetjük a következő tételt: A sík 9 pontja által kifeszített hárompontú egyenesek számának a maximuma 10.
Ezt a tételt a múlt század végén fedezte fel Sylvester. Az ő eredeti bizonyítását a rendelkezésemre álló irodalomban nem sikerült megtalálnom.
Érdekes megjegyezni, hegy azt a speciális tételt, amivel itt ellentmondásra jutottunk, ti. hogy nem helyezhető el a síkban 9 pont és 12 egyenes úgy, hogy az egyenesek mindegyike három-három ponthoz és a pontok mindegyike négy-négy egyeneshez illeszkedjék, már Maclaurin skót matematikus felfedezte 1798-ban.
3. Ezek után áttérünk az új, Erdős-féle probléma tanulmányozására.
,,Adott pont n-es esetén mekkora a négypontú egyenesek maximális száma, az M ?''
Először konkrét esetekkel próbálkozunk (kísérletezés). Ha n=4, akkor nyilván M=1. Sőt n=5,6 esetén is M=1. Ha már n=7, akkor M=2.
Az n növekedésével rohamosan elbonyolódnak a lehetséges viszonyok, és ugrásszerűen növekszik a különféle helyzetlehetőségek száma.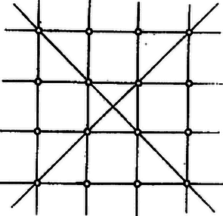
 
 
7. ábra
 

Vegyük csak az n=16 pont esetét. Az első sejtés az, hogy M=10 (7. ábra). Nem könnyű ezt a sejtést, jobb ellenpéldát találva, megcáfolni. Pedig egy szabályos ötszög egy lényegesen jobb alakzat megtalálásához vezet (8. ábra). Itt a 16 pont 15 négypontú egyenest feszít ki. Az a sejtésünk támad, hogy ez a legjobb eset, vagyis most M=15.
A négypontú egyeneseket tekintve, ennek az ábrának az adott pontjai közt vannak háromegyenesű és ötegyenesű pontok, mégpedig szám szerint 10 és 6. Hogyha a pontok szerint számlálnánk meg az illeszkedéseket, most
3⋅10+5⋅6=4⋅15=60
adódnék. Az a sejtésem, hogy 16 pont esetén ez az ábra az, mely a négypontú egyenesek maximális számát szolgáltatja.
A 2. szakaszban bemutatott módszer e sejtés bizonyítása (vagy esetleg cáfolata) céljára még nem kielégítő. A 16 pontú alakzat négypontú egyeneseire nézve csak annyit tudunk, hogy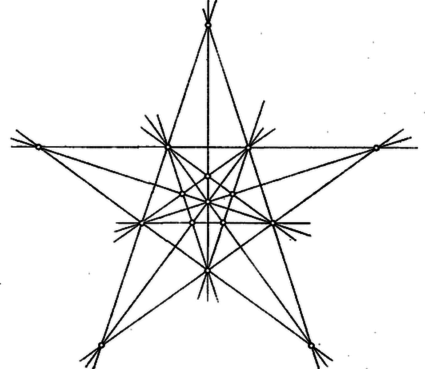
15≤M≤19.
Ez pedig még igen durva ,,becslési tétel''. Nem is részletezzük itt tovább. Mindenesetre az eddigiekből is látható, hogy általában n pont esetén a megfelelő M-re vonatkozólag nem könnyű dolog valami sokat mondó összefüggést megsejteni. Arra kezd az ember gyanakodni, hogy az n növekedésével az M-nek nem valami erős növekedése jár együtt.
 
 
8. ábra
 

Erdős az idézett cikkben a következő két sejtést említi: .. ,,én azt hiszem, hogy nagy n-re e maximum [vagyis M] sokkal kisebb nagyságrendű lesz, mint n2, talán kisebb, mint cn egy alkalmas c állandóval''.
Az idézett sejtés második felét a következőkben megcáfoljuk. (Az első fele valószínűleg igaz, sőt egy alsó korlátot is sikerült megállapítanom, amely nem is javítható. Erről azonban a felhasznált erősebb eszközök miatt egyelőre nem beszélhetek.)
 

4. Tegyük fel, hogy igaz a következő segédtétel:
Ha van egy Γ alakzat, mely n pontból áll és e pontok pontosan m négypontú egyenest feszítenek ki, akkor a Γ-ból leszármaztatható egy olyan Γ', melyre nézve
n'=4n,m'=4m+n
teljesül.
(E cikk utolsó szakaszában be fogjuk bizonyítani e segédtétel állítását is.)
Miként Γ-ból a Γ', Γ'-ből a Γ'', Γ''-ből a Γ'''..., származtatható. Most táblázatba foglaljuk a pontok és négypontú egyenesek számának fázisról fázisra való alakulását. Hogyha a Γ kiindulási alakzatban n=1, akkor m=0, és a táblázat:
|n|mΓ-ban|1|0Γ'-ben|4|1Γ'',,|42|4+4=2⋅4Γ''',,|43|4⋅2⋅4+42=3⋅42ΓIV,,|44|4⋅3⋅42+43=4⋅43ΓV,,|45|4⋅4⋅43+44=5⋅44ΓVI,,|46|4⋅5⋅44+45=6⋅45      és       így      továbbΓk-ban|4k|k⋅4k-1
Vagyis ha n=4k(k=0,1,2,...), akkor
Mm≥mn=k⋅4k-14k=k4.
Ez azt jelenti, hogy az M/n hányados ‐ Erdős sejtésének nem felel meg ‐ az n növekedése során bármely természetes számon túl növekszik.
5. Végül pedig bebizonyítjuk, hogy a segédtétel állítása valóban igaz.
Az n pontból álló Γ alakzat, amint tudjuk, legfeljebb n(n-1)/2, vagyis véges számú egyenest feszít ki. Legyen az x egyenes olyan (különben tetszőleges) állású, mely a kifeszített egyenesek egyikével sem párhuzamos. Tekintsünk egy K kört, melynek a Γ minden pontja a belsejében van. Ez a Γ egy ún. fedőköre.
Tekintsük a K két az x-szel párhuzamos érintőjét, az x' és x'' egyeneseket. Mozgassuk el ezeket az egyeneseket reájuk merőleges, őket a kört metsző helyzetbe vivő eltolással mindaddig, míg először ütköznek bele a Γ egy pontjába. Így a Γ-t bezártuk egy párhuzamosokkal határolt ún. támaszsávba. A származtatásból és x állása megválasztásából következik, hogy a támaszsáv határegyenesei a Γ-nak csak egy-egy pontját tartalmazzák; továbbá az is következik, hogy a Γ-nak a sáv belsejében elhelyezkedő pontjain át egy-egy a sávval párhuzamos egyenes halad, s az ilyen egyenesek sem tartalmaznak további pontot a Γ-ból.
A sáv x1,x2,...,xn egyeneseinek bármelyikét a Γ kifeszítette egyenesek bármelyike metszi. E metszéspontok a végesben vannak, ennélfogva a sávból két reá merőleges egyenessel olyan ABCD=Θ téglalapot vághatunk ki, mely a szóban forgó metszéspontokat tartalmazza (9. ábra).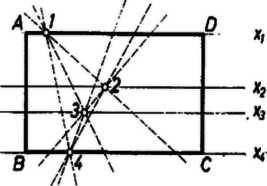
 
 
9. ábra
 

Toljuk el a Θ téglalapot a benne foglalt Γ-val együtt addig, hogy az eltolással nyert Θ* teljesen el legyen választva a Θ-tól, az eltolást a sáv irányában végezve. Most a Γ és Γ* egybefogásával adódó Γ1 alakzatnak már 2n pontja van. Ezek a Γ és Γ* kifeszítette egyeneseken kívül újabb egyeneseket is létesítenek: a kétpontú x1,x2,...,xn egyeneseket és azokat az ugyancsak kétpontú egyeneseket, amelyek a Γ egy pontját a Γ* pontjával kötik össze, de az x-szel nem párhuzamosak. Ez utóbbi kétpontú egyenesek a végesben metszik az x1,x2,...,xn egyeneseket. Ezeket a metszéspontokat a Θ és Θ*-gal együtt magába záró A1B1C1D1=Θ1 téglalap a sávból kivágható. A származtatásból nyilvánvaló, hogy a Γ+Γ*=Γ1 pontalakzatban négypontú egyeneseket a Γ és a Γ* négypontú egyenesei alkotják, tehát szám szerint 2m egyenes (10. ábra).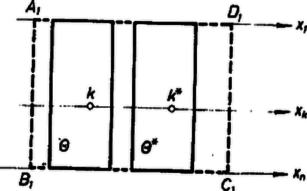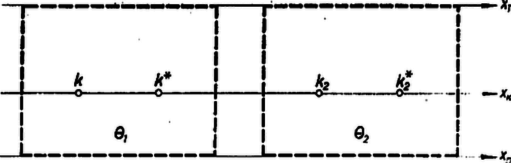
 
 
10. ábra
 

 
 
11. ábra
 

Most az elmondott származtatást megismételjük úgy, hogy a Θ szerepét a Θ1 vegye át (11. ábra).
Toljuk el Θ1-et a tőle elválasztott Θ2-be, vele együtt Γ1-et Γ2-be. Az összetett Γ1+Γ2=Γ' pontalakzat 2⋅2n=4n pontból áll. Az általa kifeszített négypontú egyenesek: a Γ1 és a Γ2 négypontú egyenesei, továbbá az x1,x2,...,xn egyenesek. Tehát a Γ' négypontú egyeneseinek száma 2m+2m+n=4m+n. Ezzel a segédtétel bizonyítását be is fejeztük.
 
 Kárteszi Ferenc