Cím: Megjegyzések a "Néhány elemi geometriai problémáról" című cikkhez
Szerző(k):  Erdős Pál 
Füzet: 1963/január, 1 - 2. oldal  PDF  |  MathML 
Témakör(ök): Szakmai cikkek

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Megjegyzések a ,,Néhány elemi geometriai problémáról'' című cikkhez*
 

1. A fent idézett cikkemben a 199. oldalon a következő sejtést említem. Legyen adva n pont a síkban, melyek nincsenek mind egy körön. Tekintsük az összes köröket, melyek a pontok közül hármon átmennek. Igaz-e, hogy legalább 1+(n-12) kört kapunk ? Ha n-1 pont egy körön van, akkor pontosan 1+ +(n-12) kört kapunk.
1962. július 22 és 28 között Oberwolfachban2 konferencia volt ún. diszkrét geometriáról, 3 s egy előadásomban e sejtést is megemlítettem. B. Serge professzor 4 azonban n=8 esetére azonnal ellenpéldát talált. Könnyű belátni, hogy azon síkok száma, melyek egy kockának legalább három csúcsán mennek át, 20 (ui. a kocka hat lapja, nyolc sík, mely a kocka egy-egy csúcsából kiinduló három él másik végpontjain megy át, és még hat sík, mely két-két párhuzamos lapátlón megy át). E síkok a kocka köré írt gömbből 20 kört metszenek ki. A gömb azonban levetíthető ún. stereografikus projekcióval 5 egy síkra úgy, hogy a körök képe is kör legyen, a gömb egy pontján (a vetítési centrumon) átmenő körök kivételével, amin átmenő körök képe egyenes. Ha mármost stereografikus projekciót alkalmazunk olyan vetítési centrummal, mely a 20 kör egyikén sincs rajta, úgy 8 pontot kapunk, melyek nincsenek mind egy körön, s melyek csak 20 kört határoznak meg, 1+(72) viszont 22. Így sejtésem nem lehet minden n-re igaz. Nem lehetetlen azonban, hogy elegendő nagy n-re a sejtés mégis igaz marad.
 

2. A 196. oldalon említem, hogy Sylvester kimutatta, hogy a síkban megadható n pont úgy, hogy azon egyenesek száma, melyek e pontok közül pontosan három ponton mennek át, nagyobb lehet, mint 13(n2)-cn, ahol c alkalmas, n-től nem függő állandó. Úgy véltem, hogy azon egyenesek száma, melyek e pontok közül pontosan négyen mennek át, sokkal kisebb nagyságrendű lesz, mint n2, sőt talán kisebb, mint c1n, ahol c1 egy alkalmas állandó.
Kárteszi néhány hónapja kimutatta, hogy a második sejtés biztosan nem igaz ‐, amint az a következő cikkben olvasható. Ő is valószínűnek tartja azonban, hogy ezen egyenesek száma jóval kisebb nagyságrendű, mint n2, sőt lehetségesnek tartja, hogy ezen egyenesek száma kisebb, mint c2nn.
Legyen t adott, 2-nél nagyobb egész szám, n egy t-nél nagyobb egész. Vizsgáljuk n ponthoz az olyan egyenesek számát, amelyek éppen t adott ponton mennek keresztül; igyekezzünk a pontokat úgy elhelyezni, hegy minél több ilyen ,,t-pontú'' egyenes legyen, és jelöljük az elérhető maximális számot f(t,n)-nel. Kárteszi azt is megmutatta, hogy tetszés szerint adott t mellett f(t,n)/n tetszés szerinti nagy, amint t elég nagy.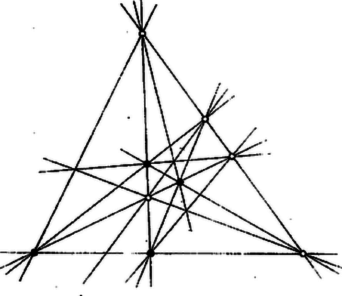
 
 

3. A 195. oldalon említem, hogy Dirac azt sejti, n pont esetén a két-pontú (,,közönséges'') egyenesek száma legalább n/2, ha n>7, azaz, f(n)-nel jelölve n pont esetén a kétpontú egyenesek minimális számát, f(n)≥n/2, ha n>7. Böröczky Károly 6 mint egyetemi hallgató megadott páros n-ekre olyan pontrendszereket, amelyekben n/2 a kétpontú egyenesek száma. Így f(n)≤n/2, tehát a Dirac sejtésében szereplő alsó korlátnál kisebb biztosan nem adható meg a kétpontú egyenesek számára ‐ legalábbis ha n, a pontok száma, páros. Ha n egy 4k+1 vagy 4k+3 alakú szám, akkor Böröczky olyan példákat talált, amelyekben a kétpontú egyenesek száma 3k (lásd n=9-re az ábrát). Ezek minden esetre kizárják már azt a lehetőséget, amit cikkemben felvetettem, hogy f(n)=n-1 legyen, ha n>n0.
A 194. oldalon a 13 lábjegyzetben utaltam Gallai tételének Motzkin által adott többdimenziós általánosításaira. Ezekhez kapcsolódva Böröczky szintén szép további eredményeket ért el, bebizonyítva többek közt Motzkin egyik sejtésének egy kissé gyengített formáját.
 

4. Végül egy hiányosságot kell pótolnom. A 196. oldal 10‐11. sorában említett ábrák n=6,7,8 esetén adnak olyan pontrendszert, amelyik csak 2n-5 egyenest határoz meg. n=9-re vegyük egy négyszög négy csúcsát (az ábrán fekete pontokkal jelölve), az átlók metszéspontját, a szemközti oldalpárok metszéspontjait és az ezeken átmenő egyenesnek a metszéspontjait az átlókkal. Ezek csak 13 egyenest határoznak meg.
 
 Erdős Pál
*Középiskolai Matematikai Lapok 24 (1962/5) 193 ‐ 201. o.

2Oberwolfach a Fekete Erdőben (Schwarzwald) fekvő nyaralóhely. Ott, egy Lorenzhof nevű villában 1947 óta gyakran tartanak matematikai konferenciákat; a villában szép matematikai könyvtár van.

3A ,,diszkrét'' jelzőt a matematikában ,,egymástól elkülönített'' értelemben szokás használni a folytonossal való szembeállításként.

4 A római egyetem tanára.

5Ilyen vetítést kapunk, ha a gömb minden pontját egy adott pontjából az ezzel átellenes ponthoz fektetett érintősíkra vagy azzal párhuzamos síkra vetítjük. Vö. pl. Kártesz F.: Síkgeometriai tételek bizonyítása térgeometriai meggondolások közvetítésével (sztereografikus projekció) K. M. L. 2 (1949 ‐ 50) 109 ‐ 117. o.

6A budapesti egyetem gyakornoka.