Kezdőlap


Cím:	1962. évi fizika OKTV feladatai és eredménye
Füzet:	1962/október, 81 - 86. oldal	PDF \| MathML
Témakör(ök):	OKTV

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Az I. forduló feladatai:

1. Sík úton

v

sebességgel haladó jármű egyenletes lassulással

s

útszakaszon fékezhető le. Mekkora hajlásszögű lejtőn marad meg nyugalomban a jármű befékezett állapotban ugyanilyen minőségű úton? (A közegellenállástól eltekintünk.)

Megoldás: Az

s

fékútból és a kezdeti

v

sebességből kiszámítható a fékezés negatív gyorsulása

v = \sqrt[]{2 a s}

alapján:

a = \frac{v^{2}}{2 s}

. A fékeződés negatív gyorsulása

a = μ g

, ha

μ

a súrlódási együttható. Ezeket egyenlővé téve a súrlódási együttható:

\begin{matrix} μ = \frac{v}{2 g s} . \end{matrix}

(1)

Így határozható meg a fékútból és a kezdeti sebességből annak a súrlódási együtthatónak a számértéke, amely a kocsit lelassította a vízszintes úton (1. ábra).

1. ábra

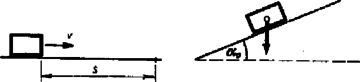Ferde lejtőre helyezett

G

súlyú ládát

G sin α

erő mozgat lefelé a lejtő mentén, és

G cos α

erő nyom merőlegesen hozzá a lejtőhöz. Ezért a súrlódási erő

μ_{1}

súrlódási együttható esetében

μ_{1} G cos α

. A láda akkor marad meg nyugalomban a lejtőn, illetve végez rajta egyenletes mozgást, ha a mozgató erő egyenlő a súrlódási erővel:

G sin α_{0} = μ_{1} G cos α_{0}

, innen annak a lejtőnek a szöge, amelyen a tárgy éppen nyugalomban marad:

\begin{matrix} tg α_{0} = μ_{1} . \end{matrix}

(2)

Ezek után a következő esetek lehetségesek. Ha szánkóról van szó, vagy a sík úton is ugyanúgy teljesen befékezett kocsit lódítunk meg, amilyent a lejtőre helyezünk, akkor

μ = μ_{1}

és

\begin{matrix} tg α_{0} = \frac{v^{2}}{2 g} : s, \end{matrix}

vagyis e lejtő hajlásszögének tangense a

v

sebességgel történő függőleges felfelé hajítás emelkedési magasságának és

s

fékútnak a hányadosa. Ugyanez érvényes részben akkor is, ha guruló kocsit hagyunk lefékeződni a vízszintes talajon, és fékezetlenül tesszük a kocsit a lejtőre. De ekkor a határszög sinusa egyenlő a súrlódási (gördülési) együtthatóval, mert a tengely mindig a csapágy aljához súrlódik, ferde lejtő esetében is, ezért a súrlódási erő mindig

μ_{1} G

. Ha a sík pályán rendesen (nem blokkolva) fékezett kocsiról, vagy guruló kocsiról van szó, de a lejtőre befékezett kocsit állítunk, akkor

μ

nem egyenlő

μ_{1}

-gyel, ezért (1) és (2) kifejezések nem kapcsolhatók össze.

2. Körpályán keringő űrhajós a Földnek mindig ugyanazon pontja felett van. A Föld mely pontjaira teljesíthető ez a feltétel? Mekkora sebességgel kering az űrhajó?

Megoldás: A körpálya középpontja a Föld középpontjában van, ezért a pálya síkjának a Föld felszínével való metszete egy főkör. A Föld felszínén levő pontok közül csak azok mozognak a Föld tengelyforgása alkalmával főkörön, amely pontok az egyenlítőn vannak. Ebből következik, hogy a feltétel csak a Föld egyenlítőjén levő pontokra teljesíthető, és az űrhajónak az egyenlítő síkjában kell keringenie.
A körpályán állandó sebességgel keringő űrhajó centripetális ereje a tömegvonzási erő. Az űrhajó tömegéhez képest a Föld tömege igen nagy, ezért a Föld középpontja állónak tekinthető. Egyenlővé tesszük a centripetális erőt a tömegvonzási erővel:

\begin{matrix} \frac{f m M}{r^{2}} = m ω^{2} r; \end{matrix}

itt

M

a Föld,

m

az űrhajó tömege,

r

az űrhajó középpontjának a Föld középpontjától való távolsága,

ω

a szögsebesség,

f

a gravitációs állandó. Rendezve:

\begin{matrix} r = \sqrt[]{\frac{f M}{ω^{2}}} . \end{matrix}

Látható, hogy a szögsebesség és a keringési rádiusz között szoros összefüggés van. A mi esetünkben

ω

-nak egyeznie kell a Föld tengelykörüli forgásának szögsebességével. Pontosan számítva a Föld tengelykörüli forgásának ideje

T = 23

óra 56 perc, a csillagnap. Ezért

ω = 7, 294 \cdot 10^{- 5} {sec}^{- 1}

, és az űrhajó pályasugara

r = 53 000 km

. Valóságos sebessége

v = ω r = 3, 865 \cdot 10^{5} cm/sec = 3, 865 km/sec

.
A feladat megoldható Kepler III. törvényével is, ha felhasználjuk a Hold keringési idejét és pályasugarát.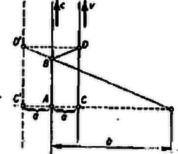

3. Állandó

c

sebességgel egyenes pályán haladó villamost a vele párhuzamosan haladó autóbusz megelőz. A két pálya távolsága

a

. Az autóbusz indexének tükörképe a villamos függőleges síkú ablakán látható. Az utca autóbusz felőli oldalán levő ház ablakában álló megfigyelő, kinek szeme az indexszel egy magasságban van, az autóbusz indexét az előzés alatt végig a villamos ablakának ugyanazon helyén látja. Mekkora sebességgel halad az autóbusz? A megfigyelő a villamos tükröző ablakának síkjától

b < a

távolságra van. Mennyiben módosul a jelenség, ha a megfigyelés emeleti ablakból történik?

2. ábra

Megoldás: A valóságos autóbusz mozgása helyett tekinthetjük virtuális képének a mozgását a villamos pályájának túlsó oldalán, ugyancsak

a

távolságban. (2. ábra.) A virtuális tükörkép ugyanolyan gyorsan mozog, mint a tárgy, ezért azalatt, míg a valóságos autóbusz

C

-ből

D

-be jut, tükörképe

C'

-ből

D'

-be kerül. Ha azt akarjuk, hogy a tükröződés a villamos ablakának ugyanazon pontján menjen végbe most is, akkor a villamosnak ezalatt

A

-ból

B

-be kellett kerülnie.

A B

és

C' D'

távolságok a sebességek arányában állanak, ezért,

v

-vel jelölve az autóbusz sebességét:

\begin{matrix} v : c = (a - b) : b . \end{matrix}

Innen az autóbusz sebessége:

\begin{matrix} v = \frac{a + b}{b} \cdot c = (1 + \frac{a}{b}) \cdot c . \end{matrix}

Az emeleti ablakból történő megfigyelés ezen mit sem változtat, mert az autóbusz virtuális képe mindenképp ugyanúgy mozog, akárhonnan nézzük is. Csak a villamos tükröző ablaka legyen elég nagy méretű, hogy rákerülhessen az a

B

pont, amelyben a visszaverődés végbemegy.

A II. forduló feladatai:

1. Áramvezető szakadásánál a két vezető végződés között szigetelő nyélre erősített fémgömbbel szállítjuk át a töltést. A fémgömb sugara

1 cm

, és percenként

54

-szer érintjük hol az egyik, hol a másik vezető végződéséhez. Hány ohm ellenállást jelent az így áthidalt szakadás? (A fémgömb kapacitását úgy számíthatjuk ki, mint szabadon álló gömbét.)

Megoldás:

ϱ

cm rádiuszú gömb kapacitása faradban

C = \frac{1}{9 \cdot 10^{11}} \cdot ϱ

. Ha a drótok végződése között

U

volt feszültségkülönbség van, akkor egy érintéskor az 1 cm rádiuszú gömbbe

\frac{U}{9 \cdot 10^{11}}

coulomb megy bele. Ezt a töltést percenként 54-szer visszük át, ezért az 1 másodperc alatt átvitt töltés, vagyis az áramerősség

I = \frac{54}{60} \cdot \frac{U}{9 \cdot 10^{11}} = \frac{U}{10^{12}}

ampere. Ohm törvénye alapján a helyzet olyan, mintha időbeli átlagban állandó erősségben

R = \frac{U}{I} = 10^{12}

ohmos ellenálláson folyna át az áram.

2. Két ingaszerűen felfüggesztett, súlyos vasrúd között fonálon teljesen rugalmatlan anyagú golyó függ. Ennek tömege a vasrudak tömegéhez képest elhanyagolható. A vasrudak tömege

m_{1}

és

m_{2}

(m_{1} > m_{2})

. Az egyik vasrudat elhúzzuk úgy, hogy súlypontja

h

-val magasabbra kerüljön, majd elengedjük. A képlékenyen alakítható golyócska az ütközés folytán összelapul. Melyik rúd ütköztetésekor lapul jobban össze a golyó, ha

h

mindkét esetben egyforma? A kapott eredmény alapján vonjunk le következtetést a kalapáccsal való alakítás hatásfokának feltételeire!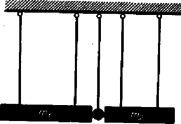

3. ábra

Megoldás: Az adott magasságból való indítás adott ütközési sebességet jelent. A közbeakasztott golyó feltétlenül rugalmatlanná teszi az ütközést, mert ez a golyó maradandó deformálódása közben nem hoz létre olyan rugalmas erőt, amely a vasrudakat ütközés után szétdobná.

m_{1}

és

m_{2}

tömegű,

c_{1}

és

c_{2}

sebességű testek rugalmatlan ütközésekor az ütközés utáni közös sebesség:

\begin{matrix} c = \frac{m_{1} c_{1} + m_{2} c_{2}}{m_{1} + m_{2}} . \end{matrix}

A rugalmatlan ütközésre nem érvényes a mechanikai energiamegmaradás törvénye, és az ütközés utáni mozgási energia kevesebb az ütközés előtti összes mozgási energiánál. A mozgási energia csökkenése:

\begin{matrix} Δ E = \frac{1}{2} \cdot m_{1} c_{1}^{2} + \frac{1}{2} \cdot m_{2} c_{2}^{2} - \frac{1}{2} (m_{1} + m_{2}) \cdot \frac{{(m_{1} c_{1} + m_{2} c_{2})}^{2}}{{(m_{1} + m_{2})}^{2}} = \\ = \frac{1}{2} \cdot \frac{m_{1} m_{2}}{m_{1} + m_{2}} \cdot {(c_{1} - c_{2})}^{2} . \end{matrix}

A mozgási energia csökkenése alakul át deformációs munkává, tehát annál eredményesebb a kalapálás, minél nagyobb a

Δ E

mennyiség. Képletünk

c_{1}

és

c_{2}

-ben szimmetrikus; így a golyócska belapulása szempontjából mindegy, hogy a kisebb vagy a nagyobb tömeget ütköztetjük hozzá ugyanazzal a sebességgel a másik, álló tömeghez. Azonban a nagyobb tömegnek csak nagyobb munkabefektetés árán tudunk ugyanakkora sebességet adni, mint a kisebbnek, ezért előnyösebb, ha a kisebb tömeg a kalapács és a nagyobb az üllő. Ha

m_{2}

a kalapács, akkor

c_{2}

ütési sebesség elérése érdekében

0, 5 m_{2} c_{2}^{2}

mozgási energiát kell ütés előtt a kalapácsnak adni. A kapott deformációs munkát előbbi képletünk adja meg

c_{1} = 0

mellett. A kalapácsolás hatásfoka a deformációs munka és a befektetett energia hányadosa: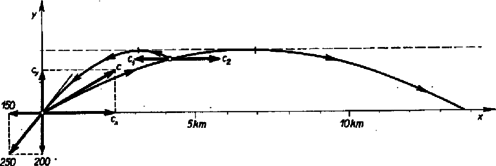

\begin{matrix} \frac{\frac{1}{2} \cdot \frac{m_{1} m_{2}}{m_{1} + m_{2}} \cdot c_{2}^{2}}{0, 5 m_{2} c_{2}^{2}} = \frac{m_{1}}{m_{1} + m_{2}} = \frac{1}{1 + \frac{m_{2}}{m_{1}}} . \end{matrix}

Látható, hogy a hatásfok annál jobb, minél kisebb az

m_{2}

kalapácstömeg az

m_{1}

üllőtömeghez képest. A valóságban az üllő tömegéhez hozzászámítandó a Föld tömege is.

3. Vízszintes terepen

30^{\circ}

-os szög alatt

400 m/sec

sebességgel lövedéket lövünk ki. A röppálya egyik pontjában a lövedék két darabra robban szét. A két darab egyszerre ér földet; az egyik pontosan a kilövés helyén csapódik be

250 m/sec

sebességgel. Milyen magasan történt a robbanás? (A légellenállás és a robbanó töltet tömege elhanyagolható, a szabadesés gyorsulását vegyük

10 {m/sec}^{2}

-nek.)

4. ábra

Megoldás: Először ismerjük meg a robbanás nélküli hajítás lefolyását. Az indítási sebesség függőleges összetevője

c_{y} = c sin α = 200 m/sec

, vízszintes összetevője

c_{x} = c cos α = 346 m/sec

. Az emelkedés ideje

c_{y} : g = 20 sec

, a hajítás teljes ideje 40 sec. Ez alatt a lövedék

346 \cdot 40 = 13 840 m

távolságig jut el. (4. ábra.) Az emelkedés magassága

c_{y}^{2} : 2 g = 2000 m

.
A lövedék szétrobbanása esetén a szilánkok közös súlypontja változatlanul repül tovább. Mivel a szétrobbanás után a két darab egyszerre ér földet, ebből következik, hogy a robbanás vízszintes irányban dobta szét a lövedék két részét, különben a sebesség függőleges összetevője a két repeszdarabnál különbözőképp módosult volna, és a két rész nem érhetett volna egyszerre földet.¹
Tehát a robbanás által adott sebesség vízszintesen, balra irányuló

c_{1}

sebességgel lökte meg a baloldali repeszdarabot. Ezért ez a baloldali repeszdarab ettől kezdve

c_{1} - 346

nagyságú sebességgel balra mozog. A robbanás nem befolyásolta a függőleges sebesség-összetevőt, tehát mindegyik szilánk földre érésekor a függőleges sebesség-összetevő ugyanaz a 200 m/sec, amellyel induláskor felfelé indult el. Tudjuk a baloldali szilánkról, hogy kiindulási pontjához 250 m/sec sebességgel érkezik vissza, mely sebesség vízszintes összetevője

c_{1} - 346

, függőleges összetevője 200 m/sec. Pythagoras tétele szerint:

\begin{matrix} 250^{2} = {(c_{1} - 346)}^{2} + 200^{2}, \end{matrix}

innen

c_{1} = 496 m/sec

, és a visszaérkezéskor meglevő sebesség vízszintes összetevője

c_{1} - 346 = 150 m/sec

.
A robbanás az indulás után

t

másodperckor következett be. E pillanattól a mozgás végéig tartó

40 - t

másodperc alatt a baloldali repeszdarab

150 (40 - t)

métert, a közös súlypont

346 (40 - t)

métert tett meg vízszintes irányban, az

x

tengely mentén. E két távolság összege a hajítás teljes távolsága, vagyis

346 \cdot 40 = 13 840

méter:

\begin{matrix} 150 (40 - t) + 346 (40 - t) = 346 \cdot 40. \end{matrix}

Az egyenlet megoldása megadja a robbanás időpontját:

t = 12, 096

sec. A robbanás helyének magassága

y = 200 \cdot 12, 096 = 1650

méter, az indulási ponttól mért távolsága

x = 346 \cdot 12, 096 = 4185

méter.
Mivel a robbanás a függőleges sebesség-összetevőre nem volt befolyással, ezért a szilánkok ugyanúgy 2000 méter magasságig emelkednek, mintha nem történt volna robbanás, és a 40. másodpercben érnek földet. A baloldali szilánk pályájának megrajzolása lehetséges az indulási pont, a robbanási pont és a 2000 méter magasságban fekvő csúcsérintő alapján. Megkönnyíti a rajzolást annak ismerete, hogy a visszatérés pillanatában olyan szögben csapódik be a baloldali szilánk, melynek tangense

200 : 150

. A jobboldali szilánk szétdobódási sebessége, a szilánkok tömegaránya a feladat adatai alapján nem határozhatók meg.

Az 1962. évi Országos Középiskolai Fizikai Verseny eredménye:

I. díj megosztva: Pellionisz András IV. o. t. (Budapest, Apáczai Csere J. g.)
Varga Lajos IV. o. t. (Budapest, Petőfi S. g.)

II. díj: Vesztergombi György IV. o. t. (Budapest, Piarista g.)

III. díj: Góth László IV. o. t. (Budapest, Könyves Kálmán g.)
Szegi András IV. o. t. (Budapest, II. Rákóczi F. g.)

Könyvjutalamban és dicséretben részesültek: 1) Kóta József IV. o. t. (Tatabánya, Árpád g.), 2) Pável Dezső IV. o. t. (Bp., Petőfi S. g.), 3) Simonovits Miklós IV. o. t. (Bp., Radnóti M. g.), 4) Niedermayer Ferenc IV. o. t. (Bp., Vörösmarty M. g.), 5) Lánc József III. o. t. (Bp., I. István g.), 6) Fazekas Patrik III. o. t. (Mosonmagyaróvár, Kossuth L. g.), 7) Kéry Gerzson IV. o. t. (Sopron, Széchenyi I. g.), 8) Dögei Ferenc IV. o. t. (Debrecen, Fazekas M. g.), 9) Gillemot László IV. o. t. (Bp., József A. g.), 10) Kálmán Béla IV. o. t. (Debrecen, Tóth Á. g.), 11) Ligeti Csák IV. o. t. (Bp., Apáczai Csere J. g.), 12) Németh István IV. o. t. (Bp., Bolyai J. g.), 13) Széchenyi Kálmán IV. o. t. (Bp., Piarista g.), 14) Máté Eörs IV. o. t. (Szeged, Radnóti M. g.)

Dicséretben részesültek: 1) Baffia László IV. o. t. (Bp., Könyves Kálmán g.), 2) Balikó Béla IV. o. t. (Sopron, Széchenyi I. g.), 3) Bánhidi János IV. o. t. (Bp., Toldi F. g.), 4) Gáspár Rezső IV. o. t. (Debrecen, Kossuth L. g.), 5) Kiss Ildikó IV. o. t. (Bp., Teleki Bl. g.), 6) Lipcsey Zsolt III. o. t. (Bp., Petőfi S. g.), 7) Mayr Endre IV. o. t. (Zalaegerszeg, Ságvári E. g.), 8) Nagy Dénes Lajos IV. o. t. (Bp., II. Rákóczi F. g.), 9) Opalényi Mihály IV. o. t. (Bp., Piarista g.), 10) Popper Gábor IV. o. t. (Bp, Bolyai J. g.), 11) Rácz Mátyás IV. o. t. (Bp., Piarista g.), 12) Reé Eőrs IV. o. t. (Bp., Piarista g.), 13) Reuss Pál IV. o. t. (Bp., József A. g.), 14) Sári Pál IV. o. t. (Bp., II. Rákóczi F. g.), 15) Szőnyi László IV. o. t. (Bp., II. Rákóczi F. g.), 16) Tungler Antal IV. o. t. (Bp., I. István g.), 17) Vidor Tamás IV. o. t. (Bp., Madách I. g.), 18) Vincze Imre IV. o. t. (Bp., Hengersor u. 34. g.), 19) Zalán Péter IV. o. t. (Aszód, Petőfi S. g.).

¹Mivel az egyik darab pontosan a kilövés helyén csapódik be, a vízszintes robbanás iránya az eredeti hajítás síkjába kell hogy essék.