Cím:	Hajítási feladatok megoldása szerkesztéssel
Szerző(k):	Vermes Miklós
Füzet:	1962/szeptember, 33 - 35. oldal	PDF  |  MathML
Témakör(ök):	Szakmai cikkek

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. Hajítási feladatok megoldása szerkesztéssel   A ferde hajítási feladatok megoldására jól használhatók a szerkesztési eljárások. A ferde hajítást meghatározza $c$ kezdősebessége és e sebesség $\alpha$ szöge. $t$ másodperckor az elhajított tárgy vízszintes koordinátája $c\cdot \text{cos}\alpha \cdot t$, függőleges koordinátája $c\cdot \text{sin}\alpha \cdot t-\frac{g}{2}\cdot t^2$, az emelkedés ideje $t_m=c\text{sin}\alpha /g$, az emelkedés magassága az elindítási pont magasságához viszonyítva $y_m=c^2\cdot \text{sin}{}^2\alpha /2g$, és a tetőzési pont vízszintes koordinátája $x_m=c^2\cdot \text{sin}\alpha \text{cos}\alpha /g$. Vízszintes síkon mérve a hajítás távolsága ennek kétszerese (1 ábra). 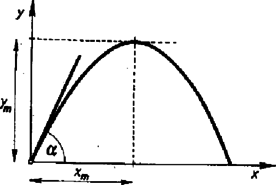    $\begin{array}{c}{\displaystyle \text{<span style="font-style: italic;">1. ábra</span>}}\end{array}$   A ferde hajítás képleteiben állandóan előfordul a 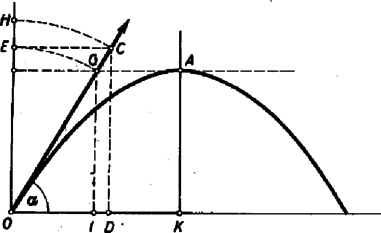$\begin{array}{c}{\displaystyle h=\frac{c^2}{2g}}\end{array}$ (1) mennyiség, amely a $c$ kezdősebességgel függőlegesen felfelé hajított tárgy emelkedési magassága. Ennek felhasználásával a ferde hajításra vonatkozó képleteink: $\begin{array}{c}{\displaystyle y_m=h\cdot \text{sin}{}^2\alpha \mathrm{,}{x}_m=2h\cdot \text{sin}\alpha \text{cos}\alpha \mathrm{.}}\end{array}$     $\begin{array}{c}{\displaystyle \text{<span style="font-style: italic;">2. ábra</span>}}\end{array}$   A szerkesztési eljárás ezek után a következő. Az adott $c$ kezdősebességből (1) szerint kiszámítjuk a hajításra jellemző $h$ mennyiséget. Ezt az elhajítás pontjában függőlegesen felmérjük (2. ábra): $h=OH$. Azután felrajzoljuk az elhajítás $\alpha$ szögét és $O$-ból mint középpontból $h$ rádiusszal megrajzoljuk a $HC$ körívet: $OC=OH=h$. Így $DC=h\text{sin}\alpha$. A $CD$ magasságot vízszintesen átvetítjük az $O$ pontban emelt merőlegesre, ekkor kapjuk az $OE=h\text{sin}\alpha$ magasságot, majd $OE$ rádiusszal ismét körívet rajzolunk $O$ középpont körül. Ez az ív az $\alpha$ szög szárát $G$-ben metszi: $OE=OG$. Az $IG$ magasság $IG=OG\cdot \text{sin}\alpha =h\cdot \text{sin}{}^2\alpha$, megadja a parabola $y_m$ tetőpontmagasságát, tehát a hajítási parabola csúcsa valahol a $G$-ponton átmenő vízszintes egyenesen fekszik. A parabola tengelyének helyét megkapjuk, ha az $OI=OG\cdot \text{cos}\alpha$ távolság kétszeresét mérjük fel: $OK=2\cdot OI$. A hajítási parabola tengelye a $K$-ponton átmenő függőleges egyenes, ennek metszéspontja a $G$-ponton átmenő vízszintessel adja meg $A$-ban a parabola csúcsát. 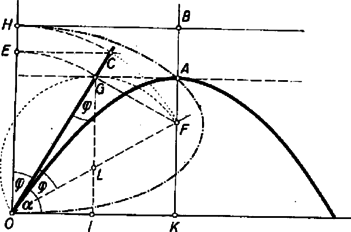    $\begin{array}{c}{\displaystyle \text{<span style="font-style: italic;">3. ábra</span>}}\end{array}$   Következik a fókuszpont megkeresése. Az $\alpha$ szög $O$-pontból kiinduló ferde szára a parabola érintője, és ez a tengellyel párhuzamos $OH$ egyenessel $\phi$ szöget zár be. Ha ugyanezt a $\phi$ szöget az $OC$ egyenes másik oldalán is felmérjük, olyan egyenest, vezérsugarat kapunk, amely átmegy a fókuszon, metszéspontja az $AK$ tengellyel a parabola $F$ fókusza. (3. ábra). További érdekességek is következnek. $L$ pont megfelezi az $OF$ távolságot, mert $I$ felezi $OK$-t. Váltószögekről lévén szó, $OGL\sphericalangle =HOG\sphericalangle =\phi$, de $GOL\sphericalangle$ is $\phi$-vel egyenlő szerkesztésünk folytán, ezért $OLG$ háromszög egyenlőszárú, és $GL=OL$. Így $L$ középponttal megrajzolható az $OGF$ félkör és az $OGF\sphericalangle$ derékszög. Az $OCE$ háromszög és $OFG$ háromszög egybevágó, mert mindegyik derékszögű, mindegyikben megtalálható a $\phi$ szög és $OE=OG$. Az egybevágóságból igen nevezetes dolgok következnek. Először is $OF=OH=h$. Tehát a fókusznak a kilövési ponttól mért távolsága megegyezik a $h$ függőleges hajítási magassággal. Minthogy ez az állítás független az $\alpha$ szög nagyságától, bebizonyítottuk, hogy az egyező sebességgel, de különböző szögekkel létrejövő parabolapályák fókuszainak mértani helye egy kör, melynek középpontja $O$ és rádiusza $h$ (a 3. ábra pontozott köre). Ezt a tételt egyébként analitikai geometriai módszerrel szokás bebizonyítani. A további következmény, hogy a $HB$ egyenes valamennyi hajítási parabola közös vezérvonala, mert $O$ pontnak, mint a parabola egy pontjának egyenlő távolságban kell lennie a fókusztól és a vezérvonaltól. A parabola csúcspontját megkapjuk, ha a fókusz és vezérvonal függőleges távolságát $\left(FB\right)$ megfelezzük $\left(A\right)$. Ezt kell tennünk minden $\alpha$ szög esetében. Ebből azonnal következik, hogy a csúcspontok mértani helye olyan ellipszis, amelynek teljes kistengelye $OH=h$ és tengelyaránya $1:2$. Szintén olyan eredmény, amelyet egyébként analitikai geometriai módszerrel szoktak bebizonyítani. 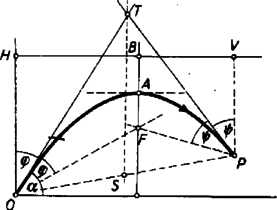    $\begin{array}{c}{\displaystyle \text{<span style="font-style: italic;">4. ábra</span>}}\end{array}$   Két példán vizsgáljuk meg, miképpen használható ilyen szerkesztéses módszer a feladatmegoldásban. Egyik feladatunk úgy szól, hogy adott $O$ pontból adott $\alpha$ szög alatt elindítva kell eltalálni $P$ pontot, és keresendő az ehhez szükséges inditási sebesség (4. ábra). Kössük össze $O$ és $P$ pontot, azután e távolság $S$ felezőpontjában rajzoljunk függőleges egyenest. Ennek az $\alpha$ szög szárával adott $T$ metszéspontja adja meg a $P$-n átmenő parabolaérintő egy pontját is. A $HOT\sphericalangle =\phi$ szöget és $VPT\sphericalangle =\psi$ szöget az érintők másik oldalára felmérve megkapjuk $F$ fókuszpontot. $O$-ban és $P$-ben a függőleges segédegyenesekre rámérve az $OH$, illetve $PV$ távolságot, megkapjuk a $HV$ vezérvonalat, azután $BF$ felezőpontjában az $A$ csúcspontot. Az $OH=h$ távolságból (1) alapján kiszámíthatjuk a $c$ indítási sebességet. 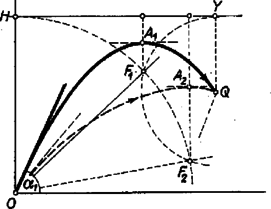    $\begin{array}{c}{\displaystyle \text{<span style="font-style: italic;">5. ábra</span>}}\end{array}$   Másik példánk úgy szól, hogy $O$ pontból adott $c$ kezdősebességgel indított ferde hajítással el kell találni az adott $Q$ pontot (5. ábra). Először $O$-ban függőlegesen felmérjük az adott $c$-hez (1)-alapján hozzátartozó $h=OH$ távolságot. $O$-ból mint középpontból $OH$ rádiusszal, $Q$-ból mint középpontból $QY$ rádiusszal egy‐egy kört rajzolunk. Ezek $F_1$, illetve $F_2$ metszéspontjai a megoldást jelentő parabolák fókuszai, mert a parabola alaptulajdonságából következik, hogy $OH=O{F}_1$, illetve $QY=Q{F}_2$. Az $F_1$ fókusztól a vezérvonalig terjedő távolság felében van az $A_1$ csúcspont. A feladatnak két megoldása van; a másik parabola $F_2$ fókuszából ugyanúgy lehet megkapni $A_2$ csúcspontját. Az elhajítás irányait a $HO{F}_1$ illetve $HO{F}_2$ szögek szögfelezői határozzák meg. $Q$ pont általában két hajítási pályán található el ugyanazon kezdősebesség mellett, egy magasabb és egy laposabb röppályán. Ha a szerkesztéshez szükséges körök nem metszik egymást, az adott $c$ sebességgel nem lehet $Q$-t eltalálni. Ha $OQ=OH+QY$, akkor csak egy parabola a megoldás, és $Q$ a hajítási parabolák burkológörbéjén fekszik. Ezen $Q$ pontok mértani helye olyan parabola, melynek fókusza $O$, paramétere $2OH$, csúcsa $H$-ban van. Így számítás nélkül, szerkesztéssel bizonyítható be a hajítási parabolák burkológörbéjének tulajdonsága (lásd KML XXI. kötet 225. oldal). A ferde hajítási feladatok egyéb eseteiben is jó áttekintést nyújthat a szerkesztéses eljárás, például az 1960. évi állami tanulmányi verseny második fordulójának 3. feladatát Bollobás Béla és Horváth Sándor szerkesztéssel oldották meg. Vermes Miklós