Kezdőlap


Cím:	Fizikai rendszerek mozgása
Szerző(k):	Fáy Árpád
Füzet:	1962/március, 129 - 132. oldal	PDF \| MathML
Témakör(ök):	Szakmai cikkek

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

A mozgásfeladatok megoldása nehezen áttekinthető, ha testek összetett mozgásáról van szó (pl. haladó és forgó mozgásról egyszerre), vagy ha sok egymással kapcsolatban levő test mozog. Ebben a cikkben egy olyan módszerrel foglalkozunk, melyet ilyen feladatok megoldására gyakran használnak a fizikában és a műszaki gyakorlatban is.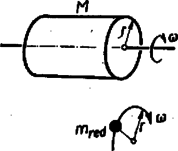
A módszer lényege: Az eredeti bonyolult mozgás helyett egy másik sokkal egyszerűbb mozgást vizsgálunk. Az elképzelt egyszerűbb mozgásban szereplő testeket gyakran modellnek nevezik. A modellben szereplő tömegeket és méreteket úgy kell megválasztani, hogy az eredeti mozgást az általunk vizsgált szempontból helyettesíteni tudja. Néhány példa:

1. ábra

Forgó henger mozgását helyettesíteni szokták egyetlen tömegpont forgó mozgásával, mely a henger sugarával egyenlő sugarú pályán mozog. Azt akarjuk biztosítani, hogy egyforma külső forgatónyomatékok hatására a henger és a modell szögsebessége pillanatról pillanatra megegyezzék. Ehhez elég azt biztosítani, hogy egy kezdeti időpillanatban a szögsebességek megegyezzenek, és minden további időpillanatban a szöggyorsulások egyezzenek. Ez a forgatónyomatékok és szöggyorsulások ismert összefüggése alapján akkor teljesül, ha a henger és a modell tehetetlenségi nyomatéka egyezik. Egyszerű számítás szerint a tehetetlenségi nyomatékok egyenlők, ha a modell tömege

m_{red} = M / 2

. Ha tehát a modell tömegét így választjuk meg, akkor mozgása helyettesíti a henger mozgását. Az

m_{red}

tömeget a henger

r

sugárra redukált tömegének nevezik. (Nincs akadálya annak sem, hogy a henger tömegét más sugarú pályára ,,redukáljuk'', csak a tehetetlenségi nyomatékok egyenlőségét kell biztosítani.) A modell bevezetése nem felesleges komplikáció, de valóban egyszerűsíti a viszonyokat. Ezt láthatjuk például abból is, hogy a henger mozgási energiája milyen egyszerűen számítható ki a modell segítségével: a hengernek és a modellnek a mozgási energiája egy időpillanatban, amikor mindkettő

ω

szögsebességgel forog, egyenlő. Ugyanis az

ω

szögsebességre való felpörgetés alatt az egyforma forgatónyomatékok nyilván egyforma munkát végeztek; és ez a munka alakult át egyszer a henger, másrészt a modell mozgási energiájává. A modell mozgási energiája egyszerűen számítható az

m_{red}

tömeg pillanatnyi

r ω

kerületi sebességéből: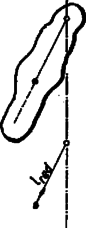

\begin{matrix} E_{m} = m_{red} \cdot {(r ω)}^{2} / 2 = (M / 2) \cdot {(r ω)}^{2} / 2. \end{matrix}

2. ábra

Második példa a fizikai inga helyettesítése matematikai ingával. Itt például a lengésidők egyenlőségét a redukált hossz helyes megválasztása biztosítja. Harmadik példa: Egy elég nagy tömegű rugóra függesztett test rezgőmozgásáról van szó. Ezt a mozgást helyettesíthetjük tömeg nélküli rugóra függesztett test mozgásával, ha a rugó tömegének bizonyos hányadát a rezgő tömeghez számítjuk. (Normális alakú rugónál a rugók tömegének

1 / 3

részét kell a rezgő tömeghez redukálni.) Sokkal bonyolultabb rezgő rendszereket is szoktak ezzel az egyszerű modellel helyettesíteni.

3. ábra

Visszatérve eredeti célunkhoz, több test összetett mozgását vizsgáljuk egy lendkerekes játékautó példáján. Az autó egyes részei csak haladó mozgást végeznek, a lendkerék haladó és forgó mozgást is végez. Látni fogjuk, hogy ez a több testből álló, többféle mozgást végző rendszer egy egészen egyszerű modell mozgásához vezet.
A játékautó futókerekének sugara

R = 1 cm

, lendkerekének sugara

r = 1, 5 cm

. A játékautó tömege

M = 140 g

, ebből

m = 40 g

jut a lendkerékre. Két fogaskerékáttétel van, így a lendkerék

i = 14

fordulatához tartozik a futókerék egy fordulata. (Ezek egy játékautóról lemért méretek kerekítve.) Kérdés: A játékautó

P = 1 kp

tolóerő hatására mekkora gyorsulással mozog, és álló helyzetből indulva mekkora lesz a sebessége

s = 1 m

út befutása után.
A súrlódást elhanyagolva az autó mozgási energiája az út végén az adatokból számítható:

P \cdot s

. Jó lenne ismerni a

v

sebességgel haladó autó mozgási energiáját. Ennek számításánál az okoz problémát, hogy a lendkerék összetett mozgása miatt a

v

sebességű haladómozgáson kívül

ω

szögsebességű forgó mozgás is van. Ilyen esetben a mozgási energiát a csak haladó és a csak forgó mozgást végző test energiájának összege adja:

\begin{matrix} E_{m} = E_{haladó} + E_{forgó} = \frac{1}{2} m v^{2} + \frac{1}{2} m_{red} {(r ω)}^{2} . \end{matrix}

Ennek igazolására képzeljük el, hogy a lendkereket egyelőre függetlenítjük a fogaskerekektől, és összetett mozgását úgy hozzuk létre, hogy először felgyorsítjuk

v

sebességre ‐ ezalatt a haladómozgás mozgási energiájának megfelelő munkát fektetünk be ‐ majd az egyenletes

v

sebességgel haladó autóban felpörgetjük

ω

szögsebességre. Márpedig az egyenletes sebességű autóban a felpörgetéshez ugyanakkora erő és energia kell, mint álló autóban. (Ezt az egészen természetes tényt mindenki érzékelheti, akinek sikerül egyenletes sebességű autóba jutni. Általános fizikai fogalmazását először Galilei adta híres relativitási elvével.)
A játékautó mozgási energiája tehát a haladómozgást végző

(M - m)

tömeg és az

m

tömegű lendkerék mozgási energiájának összege. Ez utóbbi a haladó és forgó mozgási energia összege, ahol a forgási energiát a bevezetőben említett példa szerint számíthatjuk. (A fogaskerekek és futókerekek forgási energiáját itt kicsiny tömegük és kisebb szögsebességük miatt elhanyagoltuk. Pontos számítás esetén ezeket a lendkerékhez hasonló módon számításba lehet venni.)

\begin{matrix} E_{m} = P s = \frac{1}{2} (M - m) \cdot v^{2} + \frac{1}{2} m v^{2} + \frac{1}{2} (\frac{m}{2}) {(r ω)}^{2} . \end{matrix}

Itt

v

és

ω

között egy összefüggés van. Ha a futókerék megcsúszás nélkül halad a talajon, akkor szögsebessége:

v / R

, és a lendkerék szögsebessége a fogaskerék kapcsolat miatt:

ω = i v / R

. Ezt az előző egyenletbe helyettesítve, csak

v

az ismeretlen, a tiszta másodfokú egyenletet megoldva

v ≃ 1, 5 m/sec

.
A lendkerekes autó mozgása áttekinthetőbb lesz, ha helyettesítjük egyetlen tömeg ugyanolyan sebességű haladómozgásával. Lehetséges-e ez? Előbb azt vizsgáljuk, hogy ha lehetséges, akkor mekkora legyen a modell tömege? Azt akarjuk biztosítani, hogy a játékautót és a modellt álló helyzetből egyszerre indítva, ugyanazon külső erők hatására a mozgásuk pillanatról pillanatra megegyezzék. Ez csak úgy lehetséges, ha ugyanazon

P

erő hatására

s

utat befutva a játékautó és a modell is ugyanazt a

P s

energiát raktározza el mozgási energia formájában, vagyis

\begin{matrix} \frac{1}{2} M v^{2} + \frac{1}{2} (\frac{m}{2}) {(r ω)}^{2} = \frac{1}{2} m_{red} v^{2} . \end{matrix}

ω = i v / R

helyettesítés után az egyenlet egyszerűsíthető

v^{2}

-tel. Ez nagyon fontos tény, mert ez mutatja, hagy létezik egy, a sebességtől független

m_{red}

érték. Esetünkben:

\begin{matrix} m_{red} = M + \frac{m}{2} {(\frac{r i}{R})}^{2} = 140 g + 8820 g = 8960 g ≃ 9 kg . \end{matrix}

A modellt úgy képzeljük el, mint egy játékautót, melyet a

9 kg

-os tömeg biztosítására tömör vasból készítünk szabadonfutó kerekekkel. A két autót álló helyzetből indítva, ugyanazon külső erő hatására mozgásuk pillanatról pillanatra megegyezik, az a külső szemlélő, aki nem lát be az autókba, meg sem tudja különböztetni őket. (Az előzőekből ugyan csak az következik, hogy a játékautó és a modell sebesség-út jelleggörbéje megegyezik. Általános törvény azonban a következő: Ha két mozgásnál az út-idő, sebesség-idő, sebesség-út, gyorsulás-idő, gyorsulás-út, gyorsulás-sebesség stb. jelleggörbék közül az egyik megegyezik, és egy időpillanatban a mozgásoknak ugyanazok az értékei vannak, akkor a két mozgás többi jelleggörbéje is egyezik.)
A feladatban szereplő első kérdésre így is válaszolhatunk: Az a gyorsulás, ami

P = 1 kp

erő hatására létrejön (ugyanaz, mint ami a modellen létrejön), tehát

a = P / m_{red} = 9, 81 newton / 9 kg ≃ 1, 1 {m/sec}^{2}

.
A redukált tömeggel rendelkező autó azonban mégsem helyettesíti minden tekintetben a másikat. Azonnal kiderül ez, ha az autókat lejtőre helyezzük, ahol a súlyerő mozgatja őket; vagy mérlegre helyezzük. Megállapítható, hogy a Föld vonzóereje, a gravitációs erő nem a redukált tömegre, hanem a valódi tömegre hat. A lejtőn a lendkerekes autót a valódi súlyának súlyereje mozgatja, sokkal kisebb külső erő hat rá, mint a modell autóra, ezért sokkal kisebb lesz a gyorsulása. Viszont ugyanezen oknál fogva, vízszintes síkon a súrlódás okozta lassulása lesz sokkal kisebb. Ennek a szellemes játékszernek éppen az a lényege, hogy meglökve, kis kezdeti sebessége ellenére, sokkal messzebb gurul, mint hasonló méretű közönséges játékoknál megszoktuk. (Ennek ára a meglökéshez szükséges sokkal nagyobb erőben, ill. munkában van. A mozgási energia legnagyobb része a láthatatlan lendkerékben tárolódik)
A lendkerekes autó példáját általánosítva megállapíthatjuk: Egy jármű mozgását egyszerűen tudjuk számítani a redukált tömege segítségével. A redukált tömeget úgy kapjuk, hogy a jármű haladó és forgó mozgást végző elemeinek mozgási energiáját összegezzük, és ez adja a redukált tömeggel elképzelt modell mozgási energiáját. Pl. egy gyorsvonatnál a kerekek forgó mozgásából számítható energia kb.

4 %

-a a haladó mozgás mozgási energiájának: tehát redukált tömege kb.

4 %

-kal nagyobb a valódi tömegénél.
Ez a módszer több tömegből összetett rendszerek esetén minden olyan esetben jól alkalmazható, ahol a testek között kényszerkapcsolat van (a legtöbb gép ilyen), tehát ahol az egyik test sebessége megszabja a másik test sebességét.

Fáy Árpád