Kezdőlap


Cím:	Merev test forgómozgása
Szerző(k):	Párkányi László
Füzet:	1962/január, 80 - 84. oldal	PDF \| MathML
Témakör(ök):	Szakmai cikkek

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. Az egyensúly feltétele

Szabadon mozgó test csak akkor lehet egyensúlyban, ha a rá ható erők eredője zérus. Pl., ha a testre két egyenlő nagyságú ellentétes irányú erő hat, és az erők hatásvonalai is egy egyenesbe esnek.
Más a helyzet, ha a test nem teljesen szabad, hanem csupán tengely körül végezhet forgó mozgást. Tapasztalatból is tudjuk, de kísérletileg is igazolható, hogy ekkor a test olyan esetben is nyugalomban maradhat, ha mi egyidejűleg olyan erőket fejtünk ki, melyek eredője nem zérus (az erők hatásvonalai nem esnek egy egyenesbe). Ha a test csupán tengely körül végezhet forgó mozgást (tengellyel rögzített merev test), akkor a test egyensúlyához elegendő az, ha a testre kifejtett erők eredőjének hatásvonala átmegy a tengelyen (a tengelyponton).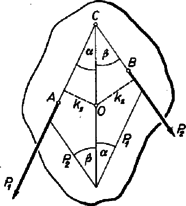

1. ábra

Ez esetben ugyanis a tengely által a testre kifejtett reakcióerő egyensúlyozza a testre kifejtett erők eredőjét. (Feltéve természetesen, hogy a tengely ill. a csapágyazás elég szilárd ehhez.) Szerkesszük meg a merev testre

A

ill.

B

pontban támadó

P_{1}

ill.

P_{2}

erők eredőjét. (Az erők támadáspontjait hatásvonaluk mentén a közös

C

pontba tolhatjuk el, az erőkkel szerkesztett paralelogramma átlója adja az eredőt. Ha a

P_{1}

ill.

P_{2}

iránya az eredővel

α

ill.

β

szöget zár be, akkor a sinus tétel szerint

\begin{matrix} \frac{P_{1}}{P_{2}} = \frac{sin β}{sin α} . \end{matrix}

Ha az eredő átmegy az

O

-val jelölt tengelyponton, akkor az

α

ill.

β

szögek sinusait másképp is kifejezhetjük. Az

O

pontból bocsássunk merőlegeseket a

P_{1}

ill.

P_{2}

hatásvonalára. Legyenek ezek

k_{1}

és

k_{2}

. A keletkező derékszögű háromszögekből

\begin{matrix} sin α = \frac{k_{1}}{O C} sin β = \frac{k_{2}}{O C}, \\ \frac{sin β}{sin α} = \frac{k_{2}}{O C} : \frac{k_{1}}{O C} = \frac{k_{2}}{k_{1}} . \end{matrix}

Ezt beírva az előző összefüggés jobb oldalába, a

\begin{matrix} \frac{P_{1}}{P_{2}} = \frac{k_{2}}{k_{1}} \end{matrix}

összefüggést kapjuk. Ezt szorzat alakjában írva

\begin{matrix} P_{1} k_{1} = P_{2} k_{2} . \end{matrix}

Csak ha ez a feltétel teljesül, akkor megy át a

P_{1}

és

P_{2}

erők eredőjének hatásvonala az

O

tengelyponton. Ez esetben a tengellyel rögzített merev test a

P_{1}

ill.

P_{2}

erők hatására nyugalomban marad.
A

P_{1} k_{1}

ill.

P_{2} k_{2}

szorzatot a

P_{1}

ill.

P_{2}

erőnek az

O

-n átmenő tengelyre vonatkozó forgatónyomatékának nevezzük.
A forgatónyomatékot egy betűvel (pl.

F

) jelölhetjük, ekkor az egyensúly feltétele így írható:

\begin{matrix} F_{1} = F_{2} . \end{matrix}

Tengellyel rögzített merev test két erő hatására akkor van egyensúlyban, ha az erőknek a tengelyre vonatkozó forgatónyomatékai ellentetten egyenlők. Még egyszer hangsúlyozzuk, hogy egyensúly esetén a merev testre ható erők eredőjét a tengely (a tengely által kifejtett reakcióerő) egyensúlyozza ki. A tengelyt tehát tetemes erő terheli. Kivéve azt az esetet, mikor a testre ható erők eredője éppen zérus (pl. erőpár).
A tengellyel rögzített merev testre ható erő a testet a tengely körül jobbra vagy balra forgatja. Az erő forgató nyomatékát ettől függően ‐ megállapodás szerint ‐ pozitív vagy negatív előjellel láthatjuk el. (Ha a jobbra forgató erő forgatónyomatékát pozitívnak vesszük, akkor a balra forgató erő forgatónyomatéka negatív vagy fordítva.) Ez esetben az egyensúly feltételét úgy is kifejezhetjük, hogy a tengellyel rögzített merev test akkor van egyensúlyban, ha a rá ható erők forgató nyomatékainak algebrai (előjellel vett) összege zérus. Ez nemcsak két, hanem tetszőleges számú erő esetére is általánosítható.
Ha a merev test csak tengely körül végezhet forgó mozgást, akkor az egyensúly feltétele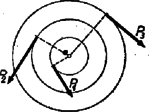

\begin{matrix} F_{1} + F_{2} + F_{3} + ... + F_{n} = 0, \end{matrix}

ahol

F_{1}, F_{2} ...

a testre ható erők előjellel vett forgató nyomatékát jelentik.

2. ábra

1. Egy korong középpontján átmenő tengely körül foroghat. A korongra 1 cm, 2 cm, 3 cm sugarú köröket rajzoltunk. A körök kerületi pontjaiban (érintő irányú)

P_{1} = 3

kp,

P_{2} = 4, 5

kp,

P_{3} = 4

kp erő hat. Egyensúlyban van-e a korong? (2. ábra.)

\begin{matrix} \begin{matrix} A & P_{1} & erő & forgatónyomatéka & F_{1} = - 3 kp \cdot 1 cm = - 3 kp cm, \\ P_{2} & ,, & ,, & F_{2} = - 4, 5 kp \cdot 2 cm = - 9 kp cm, \\ P_{3} & ,, & ,, & F_{3} = 4 kp \cdot 3 cm = 12 kp cm . \end{matrix} \\ F_{1} + F_{2} + F_{3} = - 3 kp cm - 9 kp cm + 12 kp cm = 0. \end{matrix}

A korong egyensúlyban van. Szerkesztéssel mutassuk ki, hogy az erők eredője átmegy a tengelyen!
2. Határozzuk meg az ún. differenciálcsiga esetében az egyensúly feltételeit. (A differenciálcsiga egybeépített kisebb és nagyobb korongból áll. A mozgócsiga tengelyére akasztott testet a kettős korongon átvezetett kötél ill. lánc segítségével emeljük ill. egyensúlyozzuk. Hogy a kettős csigán a lánc meg ne csúszhasson, a kettős csiga mély vájataiban még fogazásszerű kiemelkedések is vannak.)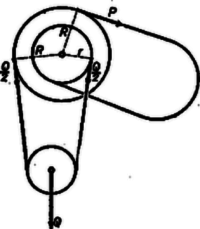

3. ábra

A kettős korongra három erő fejt ki forgatónyomatékot:

\begin{matrix} \begin{matrix} P & forgatónyomatéka & F_{1} = P R, \\ \frac{Q}{2} & ,, & F_{2} = \frac{Q}{2} r, \\ \frac{Q}{2} & ,, & F_{3} = \frac{Q}{2} R . \end{matrix} \end{matrix}

Egyensúly van, ha

\begin{matrix} F_{1} + F_{2} + F_{3} = P R + \frac{Q}{2} r = \frac{Q}{2} R = 0. \end{matrix}

Ebből a teher egyensúlyozásához szükséges P erő meghatározható:

\begin{matrix} P = \frac{Q}{2} \cdot \frac{R - r}{R} . \end{matrix}

II. Tengely körül forgó merev test energiája (forgási energia)

A merev test forgási energiája egyes tömegpontjainak mozgási energiájából származik ill. tevődik össze.
Minthogy az energia skaláris mennyiség, a forgó test energiáját a tömegpontok mozgási energiáinak egyszerű összeadásával kapjuk.
A forgó test egyes tömegpontjai általában különböző sebességgel mozognak. Ha az

m_{1}

tömegpont sebessége

v_{1}

, az

m_{2}

-é

v_{2}

, és így tovább, akkor az egyes tömegpontok mozgási energiája

\begin{matrix} \frac{m_{1} v_{1}^{2}}{2}; \frac{m_{2} v_{2}^{2}}{2}; \frac{m_{3} v_{3}^{2}}{2} ..., \end{matrix}

a forgó test energiája így

\begin{matrix} E = \frac{1}{2} (m_{1} v_{1}^{2} + m_{2} v_{2}^{2} + m_{3} v_{3}^{2} + ...) . \end{matrix}

A tömegpontok sebességét kifejezhetjük a forgás szögsebességének segítségével is, ami már a forgómozgásra jellemző állandó. Ha az

m_{1}

tömegpont a tengelytől

r_{1}

, az

m_{2}

a tengelytől

r_{2}

stb. távolságra van, akkor

\begin{matrix} v_{1} = r_{1} ω, v_{2} = r_{2} ω, v_{3} = r_{3} ω, ..., \end{matrix}

és így az energia

\begin{matrix} E & = \frac{1}{2} (m_{1} r_{1}^{2} ω^{2} + m_{2} r_{2}^{2} ω^{2} + m_{3} r_{3}^{2} ω^{2} + ...) \\ = \frac{1}{2} ω^{2} (m_{1} r_{1}^{2} + m_{2} r_{2}^{2} + m_{3} r_{3}^{2} + ...) . \end{matrix}

A zárójelben szereplő kifejezést egy betűvel (

I

) jelölve

\begin{matrix} E = \frac{1}{2} I ω^{2} . \\ Az I = m_{1} r_{1}^{2} + m_{2} r_{2}^{2} + m_{3} r_{3}^{2} + ... \end{matrix}

szorzatösszeget ‐ a későbbiekben kifejtjük, hogy miért ‐ a forgó test tehetetlenségi nyomatékának nevezzük.

III. A forgó testre ható erő munkája és a forgási energia összefüggése. A forgómozgás dinamikai alapegyenlete

Az energia-megmaradás tétele szerint a forgó test energiája is csak munkavégzés árán növelhető.
Hasson az

O

ponton átmenő tengely körül forgó testre igen kis

Δ t

ideig

P

erő. (Az erő hatásvonalának a

O

-tól való távolsága legyen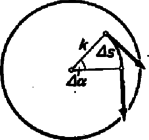

k

4. ábra

Ha eközben a test a tengely körül igen kis

Δ α

szöggel elfordul, akkor az erő irányában

Δ s = k Δ α

elmozdulás jön létre.
Az erő tehát

\begin{matrix} Δ L = P Δ s = P k Δ α = F Δ α \end{matrix}

munkát végez. [Az erő támadáspontjának az erő irányába eső elmozdulását rögtön látjuk, ha a támadáspontot az erő hatásvonalának a

O

-hoz legközelebb eső

A

pontjába toljuk el.]
E munkavégzés árán a forgási energia kevéssel (

Δ E

-vel) növekszik. Minthogy a forgási energia kifejezésében szereplő

I

tényező az elfordulás közben nyilván nem változik, az energia csak úgy változhat, hogy a forgó test szögsebessége (

ω

) változik. Legyen a szögsebesség megnövekedés

Δ ω

. Minthogy feltevésünk szerint az egész jelenség igen rövid (

Δ t

) ideig tart, a

Δ ω

is igen kicsi hányadrésze az

ω

-nak. A megnövekedett forgási energia:

\begin{matrix} E_{1} = \frac{1}{2} I {(ω + Δ ω)}^{2} . \end{matrix}

Az energia megnövekedése pedig

\begin{matrix} Δ E = E_{1} - E = \frac{1}{2} I {(ω + Δ ω)}^{2} - \frac{1}{2} I ω^{2} = \\ = \frac{1}{2} I [2 ω Δ ω + {(Δ ω)}^{2}] . \end{matrix}

De ha

Δ ω

ω

-hoz képest igen kicsi, akkor

{(Δ ω)}^{2}

még az

ω Δ ω

-hoz képest is elhanyagolhatóan kicsi. [Pl. ha

Δ ω

ezredrésze az

ω

-nak, akkor

{(Δ ω)}^{2}

már a milliomodrésze.]
Így

\begin{matrix} Δ E \sim \frac{1}{2} I 2 ω Δ ω = I ω Δ ω . \end{matrix}

Az energiatétel szerint a forgási energia megnövekedése egyenlő a végzett munkával:

\begin{matrix} Δ E = F Δ α . \end{matrix}

Kiszámíthatjuk az energiának időegységre eső megváltozását is:

\begin{matrix} \frac{I ω Δ ω}{Δ t} = \frac{F Δ α}{Δ t}, \end{matrix}

vagy

\begin{matrix} I ω \frac{Δ ω}{Δ t} = F \frac{Δ α}{Δ t} . \end{matrix}

\frac{Δ a}{Δ t}

éppen a szögsebesség,

\frac{Δ ω}{Δ t}

pedig a szögsebesség időegységre eső megváltozása, vagyis a szöggyorsulás. Jelöljük a szöggyorsulást

β

-val, akkor

\begin{matrix} I ω β = F ω, \end{matrix}

így

\begin{matrix} I β = F, vagy β = \frac{F}{I} . \end{matrix}

Ez a két kifejezés pontosan ugyanolyan szerkezetű, mint a haladó mozgásra megállapított

\begin{matrix} m a = P ill. a = \frac{P}{m} \end{matrix}

összefüggés. Ezen összefüggések dinamikai tartalma az, hogy gyorsulást csak erő hoz létre (ha

P = 0

m a = 0

azaz

a = 0

). Állandó erő ugyanazon testen állandó gyorsulást hoz létre. A létrehozott gyorsulás arányos az erővel. Adott gyorsulás létrehozásához annál nagyobb erőre van szükség, minél nagyobb a test tömege. Ez az arányosság azt fejezi ki, hogy haladó mozgás viszonylatában a tömeg a tehetetlenség mértéke.
Forgómozgásra kapott egyenleteink viszont azt mondják, hogy szöggyorsulást csak forgatónyomaték hoz létre. Ha a forgatónyomaték zérus, a szögsebesség állandó. A szöggyorsulás arányos a forgatónyomatékkal. Meghatározott szöggyorsulás létrehozásához annál nagyobb forgatónyomaték szükséges, minél nagyobb az adott test esetében az

\begin{matrix} I = m_{1} r_{1}^{2} + m_{2} r_{2}^{2} + ... + m_{n} r_{n}^{2} \end{matrix}

szorzatösszeg. Forgás esetében a tehetetlenség mértéke nem egyszerűen a tömeg, hanem az

I

tehetetlenségi nyomaték. Ezt érzékelteti a tehetetlenség nyomaték elnevezés.
A munka és a forgási energia összefüggése gyakorlati szempontból is nagy jelentőségű. Megfelelő tömegeloszlással nagymértékben megnövelhető a tehetetlenségi nyomaték, azért munkavégzés árán forgó testben nagy forgási energiát lehet kis helyen felhalmozni. Az így felhalmozott forgási energia azután munkavégzésre felhasználható. Erre szolgál motoroknál a lendkerék, melynek a dugattyú munkaüteme alatt felhalmozott forgási energiája szolgáltatja a gázkeverék komprimálásához szükséges munkát.
Érdekes példa a lendkerekes játékautó. Előzőleg nagy fordulatszámra felgyorsított lendkerék forgási energiájával hajtott autóbuszoknak közúti forgalomba állítására is történtek már próbálkozások.

Párkányi László