Kezdőlap


Cím:	Szappanhártyák minimálfelületei
Szerző(k):	Vermes Miklós
Füzet:	1962/január, 74 - 79. oldal	PDF \| MathML
Témakör(ök):	Szakmai cikkek

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Ismeretes, hogy a folyadék felszíne rugalmas hártyához hasonlóan viselkedik, és lehetőség szerint minél kisebb felületre húzódik össze. Ha drótból mint élekből mértani testek mintáit készítjük el, és ezeket szappanoldatba mártjuk, akkor a drótváz kiemelése után érdekes alakzatokat figyelhetünk meg. Például a négy szabályos háromszögből álló tetraéder esetében a szappanhártya nem a négy oldallapot borítja be, hanem hat egyenlő szárú háromszöget alkot, amelyek alapja a tetraéder $1$ ‐ $1$ éle, és amelyek a tetraéder súlypontjában találkoznak (1. ábra).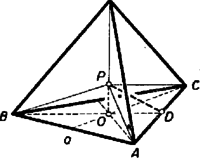

\begin{matrix} 1. ábra \end{matrix}

Ha a tetraéder alapéle

a

, akkor egy lapjának területe

a^{2} \sqrt[]{3} / 4

, négy lapból álló teljes felszíne pedig

a^{2} \sqrt[]{3} = 1, 732 a^{2}

. A tetraéder térbeli magassága

a \sqrt[]{2 / 3}

, és a súlypont ennek negyedében van, ezért

P

találkozási pont magassága az alaplap felett

P O = a \sqrt[]{2 / 3} : 4 = a / \sqrt[]{24}

. Az

A C P

egyenlő szárú háromszög magassága

D P = \sqrt[]{O P^{2} + O D^{2}}

; mivel

O D

az alaplap magasságának harmada,

O D = a \sqrt[]{3} / 6

, ezért

D P = a / \sqrt[]{8}

, és

1

egyenlő szárú háromszög területe

a^{2} \sqrt[]{2} / 8

. Tehát a

6

egyenlő szárú háromszögből álló szappanhártya teljes felszíne

3 / 4 \sqrt[]{2} \cdot a^{2} = 1, 061 a^{2}

, ami valóban kisebb, mint a tetraéder felszíne, amely

a^{2} \sqrt[]{3}

. Ilyen kérdésekkel való foglalkozást tűzött ki Lapunk egyik pályázatában, melynek eredménye ebben a számban olvasható. Lássunk néhány érdekes esetet a szappanhártyából képződő minimálfelületek köréből.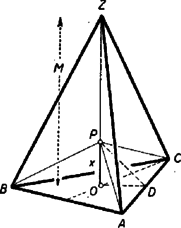

\begin{matrix} 2. ábra \end{matrix}

Foglalkozzunk a szabályos háromszög alapú egyenes gúlával (2. ábra), melynek alapéle

a

, és térbeli magassága

O Z = M

. E gúlák speciális esete a tetraéder, amikor

M = a \sqrt[]{2 / 3}

. Most a szappanhártya 3 darab, ferde síkban elhelyezkedő egyenlő szárú háromszöget (

A C P

C B P

B A P

) és 3 függőleges síkú általános háromszöget (

P C Z

P B Z

P A Z

) alkot, amelyek

P

pontban találkoznak. Független változónak

P

pont

O P = x

magasságát választjuk, és azt vizsgáljuk, adott gúlában miként változik a szappanhártya teljes felszíne, mint

x

függvénye.
Először vizsgáljuk egy függőleges és egy ferde síkú háromszög területének összegét, vagyis például

P C Z + A C P

területet. A függőleges háromszög területe két háromszög területének különbségeként állítható elő:

P C Z = O C Z - O C P = O C \cdot M / 2 - O C \cdot x / 2

, mert mindegyik háromszög magassága

O C = a \sqrt[]{3} / 3

, és az egyiknek

M

, a másiknak

x

az alapja. Hozzáadjuk

A C P

háromszög területét, amely

\frac{a}{2} \cdot \sqrt[]{x^{2} + {(\frac{a \sqrt[]{3}}{6})}^{2}}

, szorzunk 3-mal, és megkaptuk a szappanhártya teljes felszínét:

\begin{matrix} F = \frac{3 a}{2} \cdot \sqrt[]{x^{2} + \frac{a^{2}}{12}} - \frac{a \sqrt[]{3}}{2} \cdot x + \frac{a \sqrt[]{3}}{2} \cdot M . \end{matrix}

(1)

Kérdés, adott

a

és

M

méretekkel bíró gúla esetében

x

mely értéke mellett lesz ez a felszín a lehető legkisebb?
Mielőtt a minimum kereséséhez hozzáfognánk, nézzük meg az (1) alatti függvényt, és vegyük észre, hogy a gúla

M

magassága és

P

pont

x

magassága külön tagokban fordul elő. Ez azt jelenti, hogy

x

azon értéke, amely mellett

F

felszín a legkisebb, nem függ a gúla magasságától. Ez mértanilag is könnyen belátható. Az (1) képletben az első két tag az

A C P

és

O C P

háromszögek különbsége, és ez csak

P

pont

x

magasságától függ, nem pedig az egész gúla

M

magasságától. Ettől csak a harmadik tagban szereplő háromszög területe függ, amely viszont

x

-től független. Tehát akármilyen magas a gúla, a szappanhártya alsó 3 háromszöge ugyanazon magasságban levő

P

pontban találkozik. Ezt több pályázó észre is vette (Vincze Imre, Szaszovszky Géza és Török Ádám).
Ezután keressük

x

azon értékét, amely mellett az (1) szerinti hártyafelszín a legkisebb. Többféleképp kereshetjük. A differenciálszámítás könnyű, automatikus eljárást ad meg a szélsőérték megkeresésére. Ha elemi eljárást kívánunk használni, megfelelő mesterkedésekkel ugyancsak megtalálhatjuk az (1) függvény szélső értékét (lásd Hódi Endre: Szélsőérték-feladatok elemi megoldása című könyvben a 147. oldalon). Azonban most a legegyszerűbb a következő út. A gúlák sorozatába beletartozik a tetraéder is, amelyről már tudjuk, hogy a felszín minimuma

x = a / \sqrt[]{24}

-nél következik be. Minthogy a minimum feltétele nem függ

M

magasságtól, ez az érték mindegyik gúlára érvényes, a három alsó, egyenlő szárú háromszög ugyanolyan marad, akármilyen magas a gúla. (Kivétel, ha

M

kisebb, mint

a / \sqrt[]{24}

, ekkor a szappanhártya a 3 felső oldallapot vonja be; például Szaszovszky és Török figyelték meg ezt.)
Azt hihetnénk, most már gépies eljárás van birtokunkban, amellyel minden drótkeret-váz esetében meg tudjuk állapítani, milyen hártyafelszín alakul ki; tudniillik a legkisebb felszínű. Pedig a fejtörés csak most kezdődik! Mi tudjuk, hogy a legkisebb felszínnek kell megvalósulnia, de hogyan csinálja ezt a szappanlé? Matematikust tart, aki előre kiszámítja, melyik felszínalakzat a legkisebb területű, és a lé azután megvalósítja ezt? Biztosan nem így történik, hanem a drótkeret kiemelése közben a felületi feszültségből származó erők irányítják a felszín alakulását, és végül ennek az eredményét észleljük. De biztos az, hogy ily módon ugyanaz az alakzat jön létre, amelynél a felszín minimális? A tetraéder példáján tisztázzuk ezt a kérdést.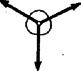

\begin{matrix} 3. ábra \end{matrix}

A felületi feszültségből származó erő a kerületre merőlegesen, a felület síkjában befelé húz. Ebből következik, hogy ha egy élben 3 sík hártyafelület találkozik, ezek feltétlenül

120^{\circ}

-os lapszöget alkotnak (3. ábra). Csak így jöhet létre a három, felületekben húzó erők egyensúlya. A

120^{\circ}

-os lapszög követelménye független a felületek alakjától, nagyságától, mert a felületi feszültség is független ezektől. Eszerint egy új alaptételünk van: három hártyafelület lapszögének

120^{\circ}

‐

120^{\circ}

nagyságúnak kell lennie. Amikor a drótvázat kihúzzuk a szappanoldatból, a felületi feszültségből származó erők úgy vezetik a síkok elhelyezkedését, hogy ez a lapszögtörvény teljesüljön. Nézzünk rá tetraéderünkre például

M

térbeli magasság folytatásának irányából: belátható, hogy a hártyafelületek valóban

120^{\circ}

-os lapszögek szerint helyezkednek el, ‐ és ugyanez érvényes mindegyik térbeli magasság körül. Tehát a tetraédernél egyszerre teljesül a minimális felszín és a

120^{\circ}

-os lapszög követelménye.

\begin{matrix} 4. ábra \end{matrix}

Néhány kiegészítő megjegyzés: A közismert karika-fonál kísérletnél is könnyen érthető, hogy a terület-feltétel és erő-feltétel egyszerre teljesül. (4. ábra.) A fonál egyik oldalán feszülő szappanhártya körív alakúra húzza be a fonalat, mert ekkor legkisebb a felszín. Ugyanekkor a fonál mentén más és más irányban hatnak a felületi feszültségből származó erők, ezért belőlük a fonál hossza mentén a fonalat feszítő erő származik, amelynek nagysága az ív görbületétől függ. Minthogy a körív görbülete mindenütt ugyanaz, a fonál hosszában fellépő feszítőerő is ugyanaz a fonál minden pontjában, ami az egyensúly feltétele. Ha a körív alakja módosulna, egyrészt megnövekedne a felszín, másrészt megbomlana a fonál mentén az egyensúly a fonál eltérő görbületei következtében. Egyes mértani testeknél az is várható, hogy más és más helyzetben emelve ki a drótvázat az oldaltól, más formájú lesz a hártyaalakzat, mert másképp fognak hozzá az erők a felszínek egyensúlyi helyzetének kialakításához. (Szaszovszky és Török figyeltek meg ilyet.) A háromoldalú gúlához hasonlóan a négyzet-, ötszög- stb. alapú gúláknál is végezhetünk számítást (lásd az ebben a számban kitűzött feladatokat).

Még megvizsgálunk egy-két alakzatot, közöttük elsőnek az oktaédert (5. ábra). Az oktaéder szappanoldatból kiemelt drótvázára igen érdekes hártya feszül: a középpontból a csúcsokhoz egy-egy deltoidlap indul, a deltoid hosszabb éle és az oktaéder oldalélei között 3 ‐ 3 egyenlő szárú háromszög helyezkedik el. Az idom megértése eléggé próbára teszi a térszemléletet.

\begin{matrix} 5. ábra \end{matrix}

Legjobb abból kiindulni, hogy az oktaéder

K

középpontjából az oktaéder minden második oldallapja felé merőleges egyenes indul; ennek

K S = x

hosszát fogjuk független változónak tekinteni. Ez a négy, egyenként

x

hosszúságú távolság úgy helyezkedik a középpont körül, mint a szénatom négy vegyértéke az atommag körül, vagyis mint egy tetraéder középpontjából a csúcsok felé húzott egyenesek. E

4

darab

x

hosszúságú távolság

Q

R

S

T

végpontjait egyenesekkel kötjük össze a legközelebbi három oktaédercsúcs ponttal. Így

6

deltoid keletkezik (

K S Y T

K T H Q

K Q X R

stb.), amelyek közül két-két szemben fekvő síkja merőleges egymásra. A deltoidok

c

hosszúságú hosszabb oldalai (például

S Y = c

) az oktaéder éleivel egyenlő szárú háromszögeket alkotnak (

S J Y

S I J

S I Y

stb.). Az oktaéder mindegyik éle felé vezet egy ilyen egyenlő szárú háromszög. Ha az alakzatra az oktaéder egyik lapja felől tekintünk rá, akkor kétféle látványban lehet részünk. Négy lap (például

J G X

) felől rátekintve három egyenlő szárú háromszögből álló bemélyedést látunk, a másik négy lap (például

G H X

) felől rátekintve egy mély üreget látunk, amelyet felváltva határol

3

egyenlő szárú háromszög és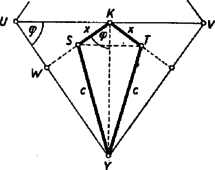

3

deltoid.

\begin{matrix} 6. ábra \end{matrix}

Keressük, hogy

x

mekkora értéke mellett lesz az oktaéderben kialakuló hártyafelszín területe a lehető legkisebb. Ragadjuk ki az oktaéder függőleges síkmetszetének alsó felét,

U Y V

-t (6. ábra). Ebben benne fekszik a

K S Y T

deltoid. Ennek

x

oldala ugyanazt a

φ

szöget zárja be a

K Y

tengellyel, mint amekkora két szomszédos oktaéderlap lapszögének a fele, például

Y U K ∢

. Erről a szögről ismeretes, illetve könnyen kiszámítható, hogy

sin φ = \sqrt[]{2 / 3}

, és

cos φ = 1 / \sqrt[]{3}

, mert

K Y = a \sqrt[]{2} / 2

, és

U K = a / 2

. A deltoid területe

\begin{matrix} 0, 5 \cdot K Y \cdot S T = \frac{a \sqrt[]{2}}{2} \cdot x \cdot sin φ = \frac{a x}{\sqrt[]{3}} . \end{matrix}

A deltoid hosszabb oldala

\begin{matrix} c = S Y = \sqrt[]{x^{2} sin^{2} φ + {(K Y - x \cdot cos φ)}^{2}} = \sqrt[]{\frac{a^{2}}{2} - \sqrt[]{\frac{2}{3}} \cdot a x + x^{2}} . \end{matrix}

Áttérve az egyenlő szárú háromszögre, melynek alapja

a

és szára

c

, e háromszög magasságára Pythagoras tétellel a

\begin{matrix} \sqrt[]{\frac{a^{2}}{4} - \sqrt[]{\frac{2}{3}} \cdot a x + x^{2}} eredményt kapjuk, területe pedig \end{matrix}

\frac{a}{2} \cdot \sqrt[]{\frac{a^{2}}{4} - \sqrt[]{\frac{2}{3}} \cdot a x + x^{2}}

. Az oktaéderben kialakuló teljes hártyafelszín

6

deltoidból és

12

háromszögből áll, vagyis

\begin{matrix} F = 2 \sqrt[]{3} \cdot a x + 6 a \cdot \sqrt[]{\frac{a^{2}}{4} - \sqrt[]{\frac{2}{3}} \cdot a x + x^{2}} . \end{matrix}

(2)

Ennek minimumát úgy találjuk meg, hogy

4

-gyel osztjuk, és alkalmazzuk ezt a helyettesítést:

x = - ξ + a / \sqrt[]{6}

. Ennek elvégzésével:

\begin{matrix} \frac{F}{4} = \frac{a^{2}}{2 \sqrt[]{2}} - \frac{a \sqrt[]{3}}{2} \cdot ξ + \frac{3 a}{2} \cdot \sqrt[]{ξ^{2} + \frac{a^{2}}{12}} . \end{matrix}

Ennek a változó része megegyezik (1) változó részével, tehát szélsőértéke is ugyanakkor van, vagyis, ha

ξ = \frac{a}{\sqrt[]{24}}

, de akkor

x = - \frac{a}{\sqrt[]{24}} + \frac{a}{\sqrt[]{6}} = \frac{a}{\sqrt[]{24}}

. Tehát az oktaéderben keletkező hártya minimumának feltétele, hogy

x = S K = \frac{a}{\sqrt[]{24}}

legyen. Mivel

W K = \frac{a}{2} \cdot sin φ = \frac{a}{2} \cdot \sqrt[]{\frac{2}{3}} = \frac{2 a}{\sqrt[]{24}}

, tehát

S

-pontnak,

x

végpontjának az oktaéderlap középpontjától való távolsága a középpont és az oktaéderlap távolságának felében van, így

W S = x = \frac{a}{\sqrt[]{24}}

. Ez igen nagy eredmény: azt jelenti, hogy idomunk három egyenlő szárú háromszöge ugyanolyan alakú, ahogyan azt a tetraédernél és a szabályos háromszögalapú gúla alaplapjánál megismertük. Ebből következik, hogy minden lapszög

120^{\circ}

-os, és a felületminimum feltétele ugyanarra vezet, mint az erőegyensúly feltétele.

Az oktaéderben keletkező hártyafelszín nagyságát a minimum esetében megkapjuk ha

x = a / \sqrt[]{24}

-et helyettesítünk (2)-be; az eredmény

2 \sqrt[]{2} a^{2}

. Az oktaéder 8 lapjának teljes felszíne

2 \sqrt[]{3} a^{2}

, ami az előbbinél nagyobb. A pályázók közül Jánossy András, Jánossy István, Kulin György és Lipcsey Zsolt munkaközössége helyesen ismeri fel, hogy a kisebb deltoidátló hossza az oldalél harmadrésze (amint az előbbi

x

-értékünkkel azonnal következik).

\begin{matrix} 7. ábra \end{matrix}

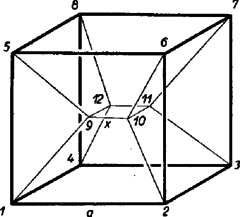Következik a kocka esete. Itt középen kis négyzet alakul ki, amelyhez

8

trapéz csatlakozik (például

1

2

10

9

) és ezek közé függőlegesen

4

egyenlő szárú háromszög áll be (például

2

6

10

). Válasszuk független változónak a kis négyzet oldalhosszúságát (7. ábra). Ekkor a trapézok magassága

\sqrt[]{{(\frac{a - x}{2})}^{2} + {(\frac{a}{2})}^{2}}

, a háromszögek magassága

\frac{a - x}{2} \cdot \sqrt[]{2}

, és a hártya teljes felszíne

\begin{matrix} F = x^{2} + 2 (a + x) \cdot \sqrt[]{2 a^{2} - 2 a x + x^{2}} + \sqrt[]{2} \cdot a (a - x) . \end{matrix}

(3)

A szélsőérték keresése harmadfokú egyenletre vezet. Ha

F

-et mint

x

függvényét grafikusan ábrázoljuk, a rajzban

x = 0, 073 a

-nál jelentkezik egy gyenge minimum. Ekkor a felszín

4, 24253 a^{2}

volna. Ezt a minimumot találta grafikus ábrázolással a Jánossy-féle munkacsoport. Ha a

120^{\circ}

-os lapszögek törvénye alapján indulunk el, arra az eredményre jutunk, hogy a kis négyzet sarkából kiinduló él mentén akkor találkozik a három sík (

2

trapéz és

1

háromszög)

120^{\circ}

-os lapszögekkel, ha a kis négyzet élhosszúsága nulla, vagyis ha nincs középen négyzet, és az egész felszín

12

háromszöggé egyszerűsödik. Ilyenkor a hártyafelszín

4, 24266 a^{2}

, vagyis egy kicsit több, mint előbb. Eszerint a kockánál nem teljesülhet egyszerre a legkisebb felszín és az erőegyensúly feltétele. És mit csinál a szappanhártya? A felsorolt két eset közül egyiket sem választja. A kis négyzet kialakul, de élhossza 5 pályamunka egybehangzó adatai szerint

0, 2 a

és

0, 3 a

között van. Hogyan lehet ez? Minden valószínűség szerint az élek és felületek kis mértékben görbültek, és olyan alakzat keletkezik, amelynél egyszerre teljesül mindkét törvény. Érdekes az I. István gimnázium fizikai szakkörének megfigyelése: ha a kockában drótból megvan egy testátló, akkor a

12

háromszögből álló felszín jön létre.
Ez a probléma vezet utolsó példánkhoz, amely görbült minimálfelület. Két párhuzamos drótkarikából álló szerkezetet mártunk szappanlébe, az idomot kiemeljük a folyadékból, és a középen keletkező körlapot átszúrjuk, hogy csak a palást mentén maradjon hártya. Görbe felszín alakul ki a két drótkarika között, úgynevezett katenoid. Ilyen felszínt kapunk, ha egy láncgörbét forgatunk az

x

-tengely körül. Bebizonyítható, hogy ez a felszín kisebb, mint a hengerpalást felszíne. Bár egyenes alkotók helyett görbékkel rendelkezik, de a felület a középsík felé közelebb húzódik a tengelyhez, és így adódik, hogy a görbült felület területe kisebb, mint a hengerpalásté. És mi van az erők egyensúlyával? Görbült hártyánál a felületi feszültségek eredője a homorú oldal felé irányuló nyomást hoz létre. A mi esetünkben mi egyensúlyozza ki ezt a nyomást? Az az érdekes körülmény áll fenn, hogy mindkét oldalon egyenlő légnyomás mellett csak olyan görbült hártya létezhet, amelynek két egymásra merőleges metszete közül a felszín az egyikben domború, a másikban homorú. Ilyen furcsa alakzat a mi felületünk is. Oldalmetszetben vizsgálva a felszín kívülről nézve homorú. De nézzük felülről a felszín ugyanezen pontját: azt látjuk, hogy ez a pont egy kör alakú felületmetszeten fekszik, és most belülről látszik homorúnak a felszín ugyanazon pontja. A kétirányú görbültségből származó nyomások ellentétesek, és kiegyenlítik egymást, mert a kétirányú görbültség abszolút értékben megegyezik. Így alakul ki a két drótkarika között a láncgörbe-forgásfelület, amely a legkisebb felszín, és egyszersmind eleget tesz az erőegyensúly feltételének is. Ha a középen eredetileg kialakuló körlapot nem távolítjuk el átszúrással, két, egymással szögben találkozó görbült felület jön létre.
Ez a vázlatos áttekintés mutatja, hogy a szappanhártyákról szóló pályázat milyen érdekes problémákat érintett. Valószínű, hogy a pályázat lezárása ez esetben olvasóink körében nem a munka végét, hanem újabb érdekfeszítő kutatások kezdetét jelenti.

Vermes Miklós