Kezdőlap


Cím:	1961. évi Eötvös Loránd Fizikaverseny
Szerző(k):	Vermes Miklós
Füzet:	1962/január, 65 - 69. oldal	PDF \| MathML
Témakör(ök):	Eötvös Loránd (korábban Károly Irén)

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Az Eötvös Loránd Fizikai Társulat szeptember 30-án rendezte ez évi Eötvös fizikai versenyét Budapesten és 6 vidéki városban az idén érettségizettek számára. A versenyzők 5 óráig dolgozhattak, és bármilyen segédeszközt használhattak. Az alábbiakban ismertetjük a verseny feladatait és azok megoldását: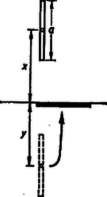
1. 1 méter hosszú, $0, 25 {grs/cm}^{3}$ fajsúlyú vékony fapálcát víz felszíne felett függőlegesen lógatunk úgy, hogy alsó vége $2$ méter magasan van a víz felett. A pálcát elengedjük. Vízbe esve milyen mélyre esik le a pálca a vízben? Minden súrlódás és közegellenállás elhanyagolandó. Mi történik, ha a pálcát $0, 5$ méter magasról ejtjük le. Mi történik, ha a pálcát a víz alól indítjuk el úgy, hogy felső vége indításkor $10$ cm-re van a víz szintje alatt? Mi történik, ha ugyanezt $0, 75 {grs/cm}^{3}$ fajsúlyú pálcával tesszük meg?
Megoldás: Ha mozgástanilag vizsgáljuk a jelenséget, akkor megállapítjuk, hogy a pálca először esést végez, amelynek végsebessége számítható. A vízbe érve az úszási helyzettől számított távolsággal egyenesen arányos erő hat rá mint a súly és felhajtóerő különbsége; ekkor nem nulla kezdősebességgel induló rezgő mozgás folyik le, végül, ha már a felső vége is elmerült, egyenletesen lassuló mozgás csatlakozik a rezgéshez. De egyszerűbb a megoldás az energiamegmaradás törvényével, annak alapján, hogy a megszerzett mozgási energia a felhajtóerő ellen végzett munkával egyenlő. Az itt közölt megoldás hasonló módszert alkalmaz.
Jelöljük a pálca hosszát $a$ -val, keresztmetszetének területét $F$ -fel, sűrűségét $d$ -vel. A folyadék sűrűsége $d_{0}$ . A pálca közepének, súlypontjának magassága induláskor a víz felett $x,$ legmélyebb helyzetében, a víz alatt $y$ . (1. ábra.) $x$ -et felfelé számítjuk pozitívnak, $y$ -t pedig lefelé.

\begin{matrix} 1. ábra \end{matrix}

Az 1. ábrán látható esetben úgy fogjuk fel a jelenséget, hogy a pálca tömege

x + y

úton leesve munkát végzett, amelynek árán a pálca helyén levő víz feljutott a felszínre. A pálca tömege

F a d

, útja

x + y

, tehát a pálca leesésekor végzett munka

F a d (x + y) g

. A pálca helyéről

F a

térfogatú,

F a d_{0}

tömegű víz jutott fel a felszínre,

y

utat megtéve, tehát ez a munkavégzés

F a d_{0} y g

. A
két munkavégzés egyenlő:

\begin{matrix} F a d (x + y) g = F a d_{0} y g . \end{matrix}

Innen a lemerülés legnagyobb mélysége:

\begin{matrix} y = x \cdot \frac{d}{d_{0} - d} . \end{matrix}

Mivel az edény felszíne igen nagy, a pálca bemerülésekor a szintmagasság nem változik észrevehetően, és a pálca helyéről felmenő víz súlypontjának útja valóban

y

.
A jobb áttekintés céljából igen jó, ha

x

y

helyett

x / a

és

y / a

változókat használjuk, amelyek a súlypont-magasságokat a pálcahossz hányadában fejezik ki. Így változóink tiszta számok, és megállapításaink bármilyen méretű pálcára vonatkoznak. Úgyszintén

d / d_{0}

sűrűséghányaddal számolunk tovább, mert a feladat szempontjából csak ez számít. Előbbi eredményünket átalakítva ezt kapjuk:

\begin{matrix} \frac{y}{a} = \frac{x}{a} \cdot \frac{\frac{d}{d_{0}}}{1 - \frac{d}{d_{0}}} . \end{matrix}

(I.)

y / a

-nak

x / a

-tól való függését koordinátarendszerben ábrázoljuk (2. ábra). Az I. alatti eredmény az origón átmenő egyenest jelent, ábránk

d / d_{0} = 0, 25

esetben mutatja ezt az egyenest (

A B

egyenes), iránytangense feladatunk első kérdése esetében

1 / 3

. Feladatunk első kérdésében

x / a = 2, 5

és

y / a = 5 / 6

\begin{matrix} 2. ábra \end{matrix}

Feladatunk érdekességei csak most kezdődnek. Téves volna azt hinni, hogy most már csak helyettesíteni kell az I. szerinti eredménybe. Ez a képlet érvénytelenné válik attól kezdve, hogy a pálca alsó helyzetében kiáll a vízből, vagyis, ha

y / a

kisebb

0, 5

-nél. Ekkor új levezetést kell végeznünk. (3. ábra.)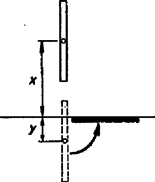

\begin{matrix} 3. ábra \end{matrix}

A pálca tömege most is

x + y

úton esik le, tehát a leeső pálca munkavégzése most is

F a d (x + y) g

, de a pálca helyéről feljutó víz tömege csak

F (\frac{a}{2} + y) d_{0}

, és ezen víztömeg súlypontja

(\frac{a}{2} + y) : 2

mélységről jut fel, így munkavégzése

\begin{matrix} F (\frac{a}{2} + y) d_{0} \cdot \frac{1}{2} (\frac{a}{2} + y) \cdot g, \end{matrix}

és a munkavégzéseket egyenlővé téve, a most érvényes egyenletünk:

\begin{matrix} F a d (x + y) g = F (\frac{a}{2} + y) d \cdot \frac{1}{2} \cdot (\frac{a}{2} + y) \cdot g . \end{matrix}

Ennek megoldása:

\begin{matrix} \frac{y}{a} = \frac{1}{2} \cdot [- (1 - 2 \cdot \frac{d}{d_{0}}) + \sqrt[]{{(1 - 2 \cdot \frac{d}{d_{0}})}^{2} + (8 \cdot \frac{d}{d_{0}} \cdot \frac{x}{a} - 1)}] . \end{matrix}

(II.)

Ez négyzetes összefüggés, ábrázolása koordinátarendszerünkben fekvő paraboladarabot ad (

B

-től

C

-ig). E képlet érvényességi területére kerül a feladat második kérdése:

x / a = 1

-nél

y / a = 0, 3

. A

B C

görbedarab továbbra is

d / d_{0} = 0, 25

mellett érvényes.

\begin{matrix} 4. ábra \end{matrix}

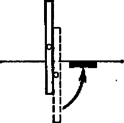II. számú képletünk érvényességi területe hamar megszűnik, amint a leeső pálca úgy indul, hogy alsó vége már induláskor is belóg a vízbe (4. ábra). A leeső pálca munkavégzését most is az előbbi kifejezés adja meg, de most

F (x + y) d_{0}

tömegű víz

(\frac{a}{2} - x + \frac{a}{2} + y) : 2

mélységből emelkedik fel:

\begin{matrix} F a d (x + y) g = F (x + y) \cdot d_{0} \cdot \frac{1}{2} \cdot (\frac{a}{2} - x + \frac{a}{2} + y) \cdot g . \end{matrix}

(Ne felejtsük el, hogy a víz szintjétől felfelé irányuló

y

negatív számként kerül az egyenletbe.) A megoldás:

\begin{matrix} \frac{y}{a} = \frac{x}{a} + 2 \cdot \frac{d}{d_{0}} - 1. \end{matrix}

(III.)

E függvény grafikus ábrázolása

45^{\circ}

-os egyenes (ábránkban

d / d_{0} = 0, 25

esetében

C

-től

D

-ig).
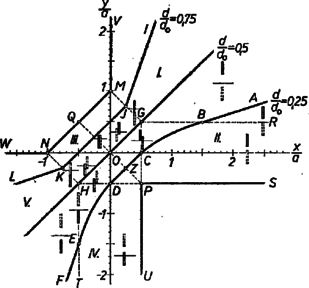
A még hátralevő két eset a legelsők inverze. A jelenség szimmetriájából is következik, hogy a kezdeti és végső pálcahelyzet felcserélhető.

x / a = 0

-tól

x / a = - 0, 5

-ig érvényes képletünk:

\begin{matrix} \frac{y}{a} = - \frac{1}{2} \cdot \frac{d_{0}}{d} {(\frac{x}{a})}^{2} + (\frac{1}{2} \cdot \frac{d_{0}}{d} - 1) \cdot \frac{x}{a} - \frac{1}{8} \cdot \frac{d_{0}}{d} . \end{matrix}

(IV.)

Ez egy álló parabola darabja

D

-től

E

-ig. Végül

x / a = - 0, 5

-től még negatívabb területek felé haladva, (

E

-től

F

irányában) az összefüggést újra az origó felé mutató egyenes tünteti fel

\begin{matrix} \frac{y}{a} = (\frac{d_{0}}{d} - 1) \cdot \frac{x}{a} . \end{matrix}

(V.)

Ide tartozik feladatunk harmadik kérdése: ha

x / a = - 0, 6

, akkor

y / a = - 1,8

.
Az úszás esetében

x / a = - y / a

, ennél kisebb

x / a

esetében a pálca kiugrik a vízből. Görbénknek ez a pont a szimmetriapontja (

Z

).
Az összefüggés képe mindaddig ilyen, amíg

d / d_{0}

kisebb, mint

0, 5

. Ha

d / d_{0}

értéke

0, 5

, akkor az összefüggést az origón átmenő

45^{\circ}

-os egyenes tünteti fel. Az I., III. és V. összefüggések egyaránt ezt adják. Ilyen sűrűségarány mellett a pálca pontosan olyan mélyre megy le a víz alá, amilyen magasról indult és fordítva.
Ha a sűrűségarány

0, 5

és 1 között van, szintén csak az I., III. és V. összefüggések szerepelnek, a II. és IV. alatti összefüggésekre nem kerül sor. Ilyenkor, ha azt akarjuk, hogy a pálca leejtés utáni legmélyebb helyzetében felül kiálljon a vízből, akkor úgy kell elindítani, hogy alsó vége induláskor beleérjen a vízbe. Az összefüggést

d / d_{0} = 0, 75

esetében a 2. ábra

I J K L

vonala tünteti fel. A feladat értelmét veszti onnantól kezdve, hogy

d / d_{0}

1-gyel egyenlő (

V M N W

vonaldarabtól balra felfelé).
A feladatban

0, 75

-ös sűrűségre vonatkozó kérdésekre a válaszok: ha

x / a = 2, 5

, akkor

y / a = 7, 5

; ha

x / a = 1

, akkor

y / a = 3

; ha

x / a = - 0, 6

, akkor

y / a = - 0, 1

.
Vizsgáljuk meg képleteink érvényességi területeit a grafikus ábrán. Az I. képlet a

V M G R

vonaltól jobbra felfelé, az V. képlet a

W N H T

vonaltól balra lefelé érvényes. A II. képlet az

R G P S

téglalapban, a IV. képlet a

T H P U

téglalapban érvényes. Végül a III. képlet használandó a

G M N H P

ötszögben. Az

S P U

-tól jobbra lefelé fekvő terület megvalósíthatatlan. A területek határvonalán mindkét érdekelt képlet ugyanazt adja. Az úszási, vagyis egyensúlyi esetek a

Q O Z P

egyenes mentén sorakoznak.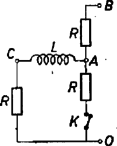

\begin{matrix} 5. ábra \end{matrix}

2. A rajz szerinti kapcsolásban a föld és

B

pont közé hosszabb idő óta

300 volt

állandó feszültségkülönbség van kapcsolva.

R

ellenállások mindegyike

100 ohm

-os és

L

tekercs önindukciója

10 henry

K

pontban a vezetéket hirtelen megszakítjuk. Kérdés: mennyivel ugrik

A

pont feszültsége közvetlenül a megszakítás után (például néhány ezred másodpercen belül)?
(Károlyházy Frigyes)

Megoldás: Az 5. ábra mutatja az elrendezést.

L

önindukciós tekercsnek nincs ohmos ellenállása. Ohm törvénye szerint az eredeti állapotban a felső ellenálláson,

B

és

A

között 2 amperes áram, az alsó ellenállások mindegyikén

C O

között és

A O

között

1

‐

1

amper folyik és

A

, valamint

C

pont feszültsége

100

volt. A hirtelen kikapcsoláskor

L

önindukciós tekercs árama egy kis darabig nem képes megváltozni, továbbra is

1

amper marad, és ekkora kell, hogy legyen a felső,

B

és

A

közötti ellenállás árama is. Tehát a megszakítás után a

B A C O

úton végig

1

amper folyik. A szakított ág ellenállásában azonnal megszűnik az áram, és a felső,

B

és

A

közötti ellenállásban azonnal

1

amperessé lesz az áramerősség, hiszen tisztán ohmos ellenállásban az áramnak nincs tehetetlenségi sajátsága. Az

1

amperes áram a

C O

közötti

100

ohmon változatlanul

100

voltos feszültségeséssel jár együtt, de a

B A

közötti

100

ohmon is

100

volt feszültségesés jön létre. Mivel

B

változatlanul

300

volton van, e pillanatban

A

pontban

300 - 100 = 200

volt jön létre. Tehát a válasz:

A

pont feszültsége

100

voltot ugrik. E pillanatban

L

önindukciós tekercsen

C

és

A

között

100

voltos feszültségkülönbség van, pedig a tekercs tökéletesen vezető fémből készült, és nincs ellenállása. Éppen ezért hirtelen növekedni kezd benne az áramerősség, olyan hirtelen, amint az az önindukciós feszültség

V = L \frac{d i}{d t}

törvényből következik. Az idők folyamán kialakuló végső állapotban az áramerősség mindegyik ellenállásban

1, 5

amper, és

A

, valamint

C

pont feszültsége

150

volt. A feszültségek és áramerősségek időbeli kialakulását mutatja a 6. ábra.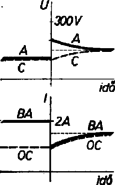

\begin{matrix} 6. ábra \end{matrix}

3. Ostornyél egyik végére vékony cérnaszálon elenyésző tömegű tollpihét kötünk, és körbe forgatjuk. Milyen pályán mozog a pihe?
(Károlyházy Frigyes)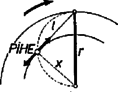

\begin{matrix} 7. ábra \end{matrix}

Megoldás: A pihére jellemző, hogy csak közegellenállása van, de nincs sem tömege, sem súlya, sem tehetetlenségi ereje. Ezért mindegy, hogy mely síkban mozog. Mozgás közben a cérna húzóerejének kell egyensúlyt tartania a pihére ható közegellenállási erővel. Időben állandó állapotban a pihe is körön mozog. Mivel a közegellenállás erő a pihe pillanatnyi elmozdulási irányával ellentétesen működik, ezért a pihe pályakörének lesz érintője a cérna iránya. (7. ábra.) A cérna másik, bothoz kötött vége nagyobb rádiuszú kört ír le. Ha tehát adva van a botvég által leírt kör rádiusza (

r

), akkor az erre rajzolt félkört a cérnahosszal (

l

) elmetszve kapjuk a pihe körének rádiuszát (

x

). Számítással:

x = \sqrt[]{r^{2} - l^{2}}

. Ha a cérnaszál hosszabb, mint a botvég körének rádiusza, akkor nincs ezen feltétel szerinti stabilis pálya.

A VERSENY EREDMÉNYE: I. díjat nyert Zakariás László (a budapesti Piarista Gimnáziumban Kovács Mihály tanítványa), II. díjat nyert Fritz József (a mosonmagyaróvári Kossuth-gimnáziumban Németh Béláné tanítványa). Dicséretet nyertek Bollobás Béla (a budapesti Apáczai Csere János gimnáziumban Csernák Emil tanítványa), Molnár Emil (a győri Révai-gimnáziumban Bőnyi Mihály tanítványa), Perjés Zoltán (a budapesti Piarista Gimnáziumban Kovács Mihály tanítványa) és Sólyom István (a budapesti Vörösmarty-gimnáziumban Óhegyi Ernő tanítványa).