| Cím: | Az 1962. évi Orsz. Középisk. Matem. Tanulm. Verseny II. fordulóján kitűzött feladatok megoldása | ||
| Szerző(k): | Bakos Tibor , Surányi János | ||
| Füzet: | 1962/december, 193 - 205. oldal |  PDF | MathML PDF | MathML |
|
| Témakör(ök): | OKTV | ||
|
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. 1. feladat. A tér pontjából három nem egy síkba eső félegyenes indul ki: , és . A és -vel meghatározott sík merőleges a és -val meghatározott síkra. A és közti és az és közti hegyes szöget ismertnek tekintve számítsuk ki az és alkotta szöget. I. megoldás. Legyen az félegyenes egy -től különböző pontja . Emeljünk -ra az pontban merőlegest és síkjában. Mivel hegyesszög, ez metszi a félegyenest egy pontban. Hasonlóan -re pontjában merőlegest állítva és síkjában, ez metszi -t egy pontban (1. ábra). 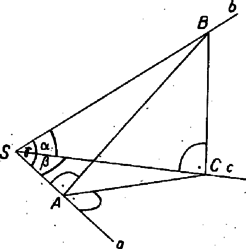 Az , , -n átmenő sík merőleges -ra, ugyanis egyenese szerkesztés szerint merőleges -ra, a egyenes pedig az síkra merőleges síkban van és merőleges a két sík metszésvonalára, így merőleges az síkra, tehát annak minden egyenesére, így -ra is. és tehát a sík két -ra merőleges egyenese, amelyek nem párhuzamosak. Így merőleges -ra, és az szög mellett, ami szerkesztés szerint derékszög, derékszög az szög is, és az szög is, mert szára az síkban van, pedig merőleges erre a síkra. Az szög a szerkesztés szerint ugyancsak derékszög. A feladat feltételei szerint , , és az szöget kell kiszámítanunk. Mostmár az , illetőleg háromszögből , , és így az háromszögből  A legtöbb versenyző több trigonometriai ismeret felhasználásával ‐ de viszont kevesebb diszkusszióval ‐ végezte el a számítást. Ilyen a következő 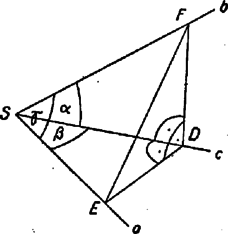 II. megoldás. Legyen a félegyenes egy -től különböző pontja , és emeljünk -re merőlegest mind az , , mind a , síkban. Mivel és hegyesszögek, ezek metszik -t -ben, ill. -t -ben (3. ábra). Az szög az és síkok hajlásszöge, tehát a háromszögben -nél derékszög van, továbbá az és háromszögek is derékszögűek. A keresett szöget tartalmazó háromszög mindhárom oldalát kifejezhetjük -vel és az ismert szögekkel: továbbá , , és így Megjegyzés. Több versenyző rámutatott, hogy hasonlóan számíthatjuk -t akkor is, ha az , és , félegyenes-párokkal meghatározott síkok szöge tetszés szerinti szög. Az szög éppen ezt a lapszöget méri, tehát 2. feladat. és két különböző természetes szám. Határozzuk meg mindazokat az természetes számokat, amelyekre az
Megoldás. I. Ha , megoldása (1)-nek, akkor az első tagból levonva -t, a másodikhoz hozzáadva Ha , nem negatív, akkor sem negatív, mert és ha Elegendő tehát azokat az értékeket vizsgálni, amelyeket az , , , értékek és tetszés szerinti nem negatív egész -ra vesz fel. Amely számok ezek közt nem szerepelnek, azokra nem oldható meg az (1) egyenlet. Megmutatjuk, hogy különböző sorokban álló számok viszont különböző maradékot adnak -vel osztva. Egy sor számai ugyanazt a maradékot adják, mint pl. az első szám. Ha a -edik és a -edik sor számai ugyanazt a maradékot adnák, akkor kezdő számaik különbsége: osztható volna -vel. Ez azonban nem lehet, ugyanis és relatív prímek, és ha egy szám egy szorzatnak osztója, de az egyik tényezőhöz relatív prím, akkor osztója a másik tényezőnek; tehát csak úgy lehetne -vel osztható, ha osztható volna -vel. Azonban is, is kisebb -nél és egyik sem negatív, így , tehát nem lehet -vel osztható. Így és különböző maradékot ad -vel osztva. Mivel sorunk van és lehetséges maradékunk (a , , , , számok), így minden maradék előfordul, és csak egyszer. Egy adott szám tehát legfeljebb egy sorban fordulhat elő és ott is csak egyszer, mert a sor egymás utáni számai állandóan nőnek. Megállapításaink akkor is érvényben maradnak, ha a sorokat bal felé is folytatjuk ismételt levonásával, hiszen az egyes sorokról csak annyit használtunk ki, hogy a szomszédos számok különbsége . Az így kiegészített táblázatban minden egész szám szerepel. Ha ugyanis tetszés szerinti egész szám, és a -adik sor az, amelynek a számai ‐ köztük is ‐ ugyanazt a maradékot adják, mint , akkor osztható -vel, tehát van olyan egész szám, amelyre , . Így a -adik sornak a -tól számított -edik száma jobbra vagy balra előjele szerint. Mivel a sorokat balra folytatva mindegyikben elegendő lépés után csupa negatív szám áll (-szori levonás után biztosan), így csak véges számú olyan pozitív egész szám van, amelyikre nincs (1)-nek nem negatív egészekből álló megoldása, és ezek a táblázat kiegészítésekor, tehát az Ha viszont , akkor az és egyenletnek ugyanazok a számpárok a megoldásai. Így ha , -ből kiindulva írjuk fel a (3)-nak megfelelő táblázatot, az abban fellépő pozitív számok -szeresei felelnek meg többszörösei közül a feladat feltételeinek. Ezek azonban éppen a (3) táblázatban fellépő pozitív számok. Az (1) egyenletnek tehát akkor nincs nem negatív egészekből álló megoldása, ha a (3) táblázatban fellépő valamelyik természetes szám, továbbá ha és legnagyobb közös osztójával nem osztható (ha e két szám nem relatív prím egymáshoz). 2. Könnyen látható az is, hogy ha , akkor és közül az egyik kielégíti a feladat követelményeit, a másik nem. Valóban, egyrészt ha volnának olyan , , , nem negatív egész számok, amelyekre Másrészt láttuk, hogy az (1) egyenletnek mindig van egész megoldása, és van olyan , , megoldása is, amelyben . Ha most az egyenletnek nincs nem negatív egészekből álló megoldása, akkor . Ekkor 3. A , , , , számoknak ezek szerint pontosan a fele elégíti ki a feladat követelményeit, tehát 3. feladat. Egy kör valamely érintőjének két pontja és . Jelöljük -nek -ra vonatkozó tükörképét -vel. Tekintsük az -ből és -ből a -hoz húzott második érintőket. Mi ezek metszéspontjának mértani helye, ha végigfut -n? Az alábbi megoldásokban a következő jelöléseket fogjuk használni: érintési pontja legyen , -nak ezzel átellenes pontja , középpontja , az -ből és -ből húzott második érintők metszéspontja , érintési pontjuk -n és . I. megoldás. Azt fogjuk megmutatni, hogy az pont minden helyzeténél a egyenes párhuzamos -val, ehhez azonban előbb megvizsgáljuk a pont lehetséges helyzeteit a körhöz és -hez viszonyítva. Van az , pontpárnak egy olyan helyzete, amelyben a -hoz húzott második érintők párhuzamosak. Ezt a pontpárt úgy kaphatjuk meg, hogy -nak az -ra merőleges átmérője végpontjaiban, (, -ben) húzunk érintőket. Ezek -ra szimmetrikus pontpárt metszenek ki -ből, mert a köztük levő sáv középvonala. Ha , a sávon kívül van, akkor , a -t tartalmazó , félkörön van, így a második érintők metszik egymást, még pedig -nek azon a partján, amelyiken van; így a háromszögnek beírt köre (4. ábra). 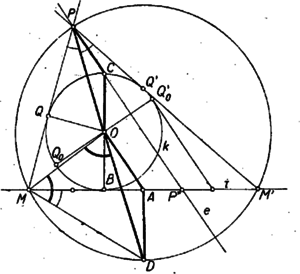 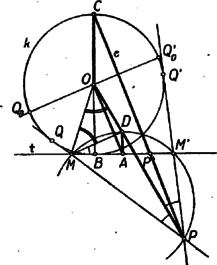 Ha , a két párhuzamos közt van, akkor , a -t tartalmazó , félkörön van, így most is metszik egymást az érintők. Ha az , pontpár közrefogja -t, akkor és is közrefogja -t a félkörön. Ekkor a érintő ellenkező partján keletkezik, mint , és a háromszög oldalához hozzáírt kör (5. ábra). Ha és egyike -be esik, és ez különbözik -tól, akkor ebből a pontból nem húzható -től különböző érintő, viszont tekinthetjük a második érintőnek is -t. A másik pont ekkor -nek -ra vonatkozó tükörképe, és ez a két második érintő metszéspontja is, tehát a mértani helynek az és mondott helyzetéhez tartozó pontja is. Ha végül az és pontok egyike és közé esik, akkor a másik pontból húzott érintőnek az érintkezési pont és a egyenes közé eső szakaszán keletkezik. Ekkor a háromszög egyik olyan hozzáirt köre, amelyik az oldal meghosszabbítását érinti (6. ábra). 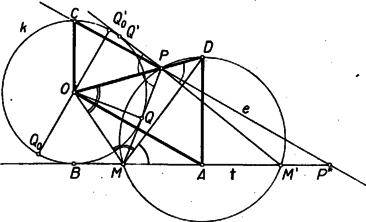 Ha egybeesik -vel, akkor is, is, az , pontpár is, így a belőlük húzott érintőpár is tükrös a egyenesre, tehát a pont ezen az egyenesen van. Az egyenes bármely a körön kívüli pontjából két szimmetrikus érintő húzható -hoz, ezek szimmetrikus , pontpárt metszenek ki -ből, amiből kiindulva éppen a kiszemelt pontot kapjuk meg. A és pontban csak egy-egy érintő húzható -hoz; az utóbbi nem metszi -t, az előbbi viszont éppen , így nem adható meg olyan pontpár, amelyikből kiindulva -t vagy -t kapnánk a mértani hely pontjaiként. Ebben az esetben tehát a egyenes -n kívüli két félegyenese a keresett mértani hely. (A és egyenes ebben az esetben egybeesik, ami megfelel állításunknak.) Tegyük fel a továbbiakban, hogy és különböző. Nyilvánvaló, hogy és felcserélésével ismét -ra tükrös pontpárt kapunk, a hozzájuk tartozó pont pedig nem változik. Így elegendő azokat a pontokat vizsgálni, amelyek az -ból -n át húzott félegyenesen levő pontokhoz tartoznak; hiszen ha a másik félegyenesen fut végig, akkor az előbbi pontokhoz tartozó mértani helyet futja be még egyszer. Térjünk most állításunk bizonyítására. Az pont a háromszög -ből induló belső vagy külső szögfelezőjén van, aszerint hogy az szakaszt érinti, vagy annak meghosszabbítását. Jelöljük a kérdéses szögfelező és a háromszög köré írt kör metszéspontját -vel. A belső szögfelező metszéspontja a -t nem tartalmazó ív felezőpontja, mivel pedig a belső és külső szögfelező egymásra merőleges, így és a két szögfelező -val való metszéspontja derékszögű háromszöget alkot. Ennek átfogója a körnek átmérője. Így a külső szögfelező a körülírt kört a belső szögfelező metszéspontjával átellenes pontban, vagyis a -t tartalmazó ív felezőpontjában metszi. Bármelyik pontból bocsátunk is merőlegest -re, az azt felezőpontjában, -ban metszi. Állításunkat úgy bizonyítjuk, hogy megmutatjuk mindegyik esetben a és háromszögek hasonlóságát. Könnyű látni, hogy az és derékszögű háromszögek hasonlók. Valóban, ha a -nél levő belső szög felezőjén van, akkor a kerületi szögek összefüggését felhasználva
Itt , mint körsugár, egyenlő -vel, állításunk igazolásához így szükségünk van annak a megmutatására, hogy . Ha a háromszög beírt köre, akkor is a háromszög belső szögfelezője, s így, mint az háromszög külső szöge Ha az oldalhoz hozzáírt kör, akkor a háromszög külső szögét felezi, s így ismét az háromszögből indulva ki Ha a háromszög oldalához hozzáírt kör, akkor is, is a háromszög megfelelő külső szögét felezi, s így ismét az háromszögből indulva ki Eszerint az háromszög -vel és -mel szemben levő szögei mindhárom esetben egyenlők, s így valóban . Ezt, továbbá az említett egyenlőséget felhasználva (1)-ből Az és háromszögek itt szereplő oldalai párhuzamosak. Az első esetben a egyenes ellenkező partján van, mint , s így és ellenkező irányban, és pedig egy irányban párhuzamos, és szintén. A második és harmadik esetben és a egyenes egy partján van, így és ellenkező irányban párhuzamos. Másrészt a második esetben az szakaszon van, a harmadik esetben a szakasz -n túli meghosszabbításán, így és is ellenkező irányban párhuzamosak. Ennek folytán az és háromszög mindhárom esetben hasonló, mert két oldaluk aránya és a köztük levő szög megegyezik, és hasonló helyzetű is. Így a harmadik oldalpár is párhuzamos: Eszerint mindig a ponton át az ( ponttól független) egyenessel párhuzamos egyenesen van. Nyilván nem lehet az egyenes körbe eső húrján. Legyen metszéspontja -vel (7. ábra), ekkor párhuzamos a háromszög oldalával és a oldal felezőpontjából indul ki, tehát a háromszög középvonala; így felezi a szakaszt, vagyis a pont tükörképe -ra, de ekkor, mint a megoldás elején láttuk, a mértani hely , pontpárhoz tartozó pontja . 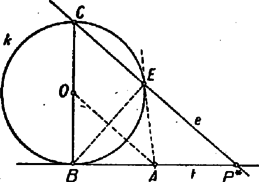 Vizsgáljuk meg végül metszéspontjait -val. A -ben húzott érintő párhuzamos -vel, nem keletkezhet tehát annak semelyik pontjából húzott érintőként, és nem megy át rajta a kör más pontjához húzott érintő sem. Így nem tartozik a mértani helyhez. A másik metszéspont nem más, mint az -ból -hoz húzott második érintő érintési pontja, ugyanis -ra tükrözve -t a tükörkép egyrészt -n van, mert annak középpontján átmenő egyenesre tükröztünk, másrészt -n, mert egy háromszög egy csúcsát a szemközti oldallal párhuzamos középvonalra tükrözve a tükörkép a szemközti oldalán van. Így tükörképe csak lehet, és az egyenes tükörképe, tehát érinti a kört. Eszerint az -ben húzott érintő -ban metszi -t. Ez a pont saját tükörképe, egybeeső , pontpárt kapunk, a belőlük húzott második érintők is egybeesnek, tehát nincs meghatározott metszéspontjuk, s így nem tartozik a mértani helyhez. A keresett mértani hely tehát a -n át -val párhuzamosan húzott (vagy -n és az -ból húzott érintő érintési pontján át, vagy -n és a pont -ra vonatkozó tükörképén át húzott) egyenesnek a -n kívül eső két félegyeneséből áll. Az első két esetben a -ből induló oldalak és közös külső érintői, pedig az egyik közös belső érintő, a harmadik esetben pedig a -n átmenő érintők a közös belső érintők, pedig az egyik külső közös érintő. Állításunk ennek folytán úgy fogalmazható, hogy két kör egy közös külső érintőjén az érintési pontok közti szakasz, és a belső érintők metszéspontjai közti szakasz felezőpontja közös, és hasonlóan egy belső közös érintőn az érintési pontok és a külső közös érintők metszéspontja közti szakasz középpontja szintén azonos. Ezt fogjuk először bizonyítani. 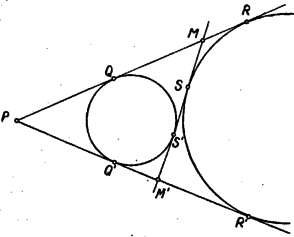 Legyen tehát két kör két közös külső érintőjének metszéspontja , az egyik érintő érintse a köröket , ill. pontban, a másik , ill. -ben (8. ábra). Egy közös belső érintő messe az előbbit egy pontban, az utóbbit -ben, és legyen az -hez közelebbi érintési pont , a másik . Ekkor az egy pontból egy körhöz húzható érintők egyenlősége folytán . Mivel még és , így kell, hogy 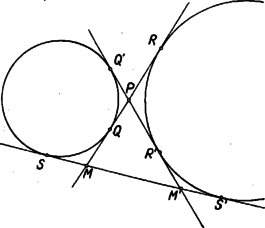 Hasonló jelöléseket használva két közös belső érintő esetén (9. ábra) Ez feladatunkra alkalmazva valóban azt adja, hogy mind a három esetben és körök és érintési pontjai egymás tükörképei az szakasz felezőpontjára nézve, és ezt akartuk belátni. az első két esetben és külső hasonlósági pontja, a harmadik esetben pedig belső hasonlósági pontjuk, így következik, hogy , és egy egyenesen vannak, ha belátjuk, hogy a mondott középpontú hasonlóságoknál a és pont mindig megfelelő pontok. Az első és második esetben és különböző oldalán van (10. ábra), így , ellenkező irányban merőlegesek -re, és tehát egyirányú párhuzamos sugarak, így a külső hasonlósági pontra nézve és a két kör egymásnak megfelelő pontjai.  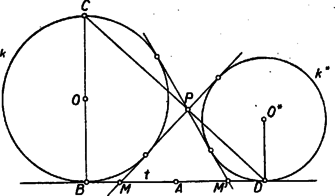 A harmadik esetben és -nek ugyanazon az oldalán van (11. ábra), így és egy irányban, és tehát ellenkező irányban párhuzamosak. most belső hasonlósági pont, erre nézve és ismét egymásnak megfelelő pontok. Ezzel bebizonyítottuk, hogy , és mindig egy egyenesen van, vagyis, mivel a és pontok nem változnak -mel, a mértani hely pontjai a egyenesen vannak. Az, hogy ennek az egyenesnek mely pontjai tartoznak a mértani helyhez, az előbbi megoldáshoz teljesen hasonlóan tárgyalható. Ezt itt nem ismételjük meg. A versenyzők legtöbbje a koordinátageometria módszereivel kereste a mértani helyet. Bemutatunk egy ilyen megoldást.
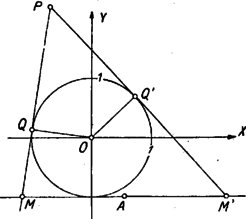 Az , ill. pontból húzott érintő érintse a kört a , ill. pontban. Ekkor
Ez az érintő átmegy -en, tehát
A metszéspont , koordinátáit kiszámíthatjuk pl. úgy, hogy az első egyenlet -szöröséből levonjuk a második -szeresét: Ismét hagyjuk figyelmen kívül egyelőre a esetet (amikor és egybeesik, s így megegyezik -val), ekkor, amennyiben ,
A keresett mértani hely pontjai tehát az
Vizsgáljuk meg, hogy (7) mely pontjai keletkeznek mint alkalmas és pontokból húzott érintők metszéspontjai. Ezek azok a pontok, amelyek koordinátái alkalmas és (valós) számokkal (4), (5) alakban írhatók. Az ilyen (és (1) szerint neki megfelelő ) értéket az -ből húzott érintő (3) egyenletéből számíthatjuk ki. Azt szerint rendezve Meg kell még vizsgálnunk a korábban a tárgyalásból kizárt eseteket, hogy tartozik-e azokhoz és milyen pontja a mértani helynek. Természetesen minden kizárt esettel együtt az helyett -re vonatkozó megfelelő esetet is tárgyalni kell, ez azonban a két pont szimmetrikus szerepe miatt nem fog külön feladatot jelenteni. Korábban figyelmen kívül hagytuk az értéket. A (7) egyenes ehhez tartozó pontjának ordinátája , és éppen láttuk, hogy ez sem tartozik a mértani helyhez. Kizártuk azt, hogy az (vagy ) pontból húzott érintő érintési pontjának (vagy ) abszcisszája legyen. Ebben az esetben az érintési pont csak vagy lehet. Az előbbi eshetőséget már éppen kizártuk. Az -ből és -ből húzott ,,második'', azaz -től különböző érintő viszont a -től különböző pontban érinti -t, kivéve, ha (ill. ) éppen a pont. Ekkor tekinthetjük ,,második'' érintőnek is a egyenest. Mivel ekkor (vagy ) , (1) miatt a másik pont a pont, és a két érintő metszéspontja is ez a pont, ami a (7) egyenes metszéspontja -vel. Ezt tehát a mértani helyhez tartozónak tekinthetjük. Ezzel egyszersmind a és esetet is megtárgyaltuk. Kizártuk végül korábban a esetet. Ekkor pl. az -ből húzott érintő (3) egyenletét -ra redukálva és -tel szorozva Ezzel bebizonyítottuk, hogy a keresett mértani hely az egyenesnek a körön kívül eső két félegyenese, ami nem más, mint az -ból húzott érintő érintési pontját és a érintési pontjával átellenes pontot összekötő húrnak a körön kívüli meghosszabbítása mindkét irányban. Megjegyzések. 1. A esetben (1)-ből , azaz , és így az -ből húzott érintő egyenlete ilyen alakban írható: 2. A két érintő egyenletéből még egyszerűbben jutunk a mértani hely egyenletéhez, ha a két érintő -ra redukált egyenletének különbségét képezzük és felhasználjuk (1)-et: 3. Sok versenyző nem kereste a számítások lehetőleg egyszerű útját, és így nem maradt kellő ideje terve teljes végrehajtására. |