Cím:	Az 1962. évi Orsz. Középisk. Matem. Tanulm. Verseny I. fordulóján kitűzött feladatok megoldása
Szerző(k):	Lukács Ottó ,  Scharnitzky Viktor ,  Surányi János
Füzet:	1962/szeptember, 7 - 10. oldal	PDF  |  MathML
Témakör(ök):	OKTV

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. Az 1962. évi Országos Középiskolai Matematikai Tanulmányi Verseny I. fordulóján kitűzött feladatok megoldása   1. feladat. Állapítsuk meg két szám negyedik hatványainak összegét, ha e számok összege $10$ és szorzata $4$. I. megoldás. Nem nehéz meghatározni a szóban forgó két számot ‐ jelöljük ezeket $x$ és $y$-nal ‐, majd negyedik hatványaik összegét. A feladat szerint $\begin{array}{c}{\displaystyle x+y=\mathrm{10,}xy=\mathrm{4,}}\end{array}$ így $x$ és $y$ a $\begin{array}{c}{\displaystyle z^2-10z+4=0}\end{array}$ másodfokú egyenlet két gyöke, vagyis $+5+\sqrt[]{21}$ és $+5-\sqrt[]{21}$ (bármelyiket tekinthetjük $x$-nek, a másik az $y$). Negyedik hatványaik összege ${\displaystyle \begin{array}{c}\hfill {\displaystyle {\left(5+\sqrt[]{21}\right)}^4+{\left(5-\sqrt[]{21}\right)}^4={\left({\left(5+\sqrt[]{21}\right)}^2\right)}^2+{\left({\left(5-\sqrt[]{21}\right)}^2\right)}^2=}\hfill \\ \hfill {\displaystyle ={\left(46+10\sqrt[]{21}\right)}^2+{\left(46-10\sqrt[]{21}\right)}^2=2\left({46}^2+{10}^2\cdot 21\right)=8432.}\hfill \end{array}}$ II. megoldás. A feladatot egyszerűbben is megoldhatjuk, anélkül, hogy a két számot kiszámítanánk. Két szám negyedik hatványainak az összegét ugyanis általában kifejezhetjük a két szám összegének ‐ jelöljük $p$-vel ‐ és szorzatának ‐ jelöljük $q$-val ‐ a segítségével: ${\displaystyle \begin{array}{c}\hfill {\displaystyle x^4+y^4={\left(x^2+y^2\right)}^2-2x^2{y}^2={\left({\left(x+y\right)}^2-2xy\right)}^2-2{\left(xy\right)}^2=}\hfill \\ \hfill {\displaystyle ={\left(p^2-2q\right)}^2-2q^2=p^4-4p^{2}q+2q^2\mathrm{.}}\hfill \end{array}}$ A $p=10$ és $q=4$ adatok behelyettesítésével: $\begin{array}{c}{\displaystyle x^4+y^4=8432.}\end{array}$ Megjegyzések. 1. A két szám negyedik hatványainak összegét az összegük és szorzatuk segítségével többféleképpen is felírhatjuk, pl. ${\displaystyle \begin{array}{c}\hfill {\displaystyle {\left(x+y\right)}^4=x^4+y^4+4x^{3}y+4x{y}^3+6x^2{y}^2=x^4+y^4+4xy\left(x^2+y^2\right)+}\hfill \\ \hfill {\displaystyle +6{\left(xy\right)}^2=x^4+y^4+4xy\left({\left(x+y\right)}^2-2xy\right)+6{\left(xy\right)}^2\mathrm{.}}\hfill \end{array}}$ Innen $x^4+y^4$-t kifejezve rendezés után ismét a fönti kifejezést nyerjük. 2. Az $x^4+y^4$ polinom nem változik meg, ha benne $x$-et és $y$-t felcseréljük, ugyanez áll az $x+y$ és $xy$ polinomokra is. Általában az $x_1$, $x_2$, $\text{...}$, $x_n$ változók egy polinomját szimmetrikus polinomnak nevezzük, ha a változói helyébe ugyanezeket a változókat egy tetszés szerinti más sorrendben írva be, a polinom nem változik meg (legfeljebb a tagok sorrendje változik). Ha $k\le n$, az $x_1$, $x_2$, $\text{...}$, $x_n$ változókból képezhető összes $k$-tényezős szorzatok összegét a változók ($k$-adfokú) elemi szimmetrikus polinomjának nevezzük. Mármost az algebra egy nevezetes tétele szerint minden szimmetrikus polinom kifejezhető a változói elemi szimmetrikus polinomjainak a polinomjaként. Ez a kifejezés (összevont alakban) a tagok sorrendjétől eltekintve egyértelmű. Ezt a kifejezést állítottuk elő a II. megoldásban, és nem véletlen, hogy ugyanarra az eredményre vezet az 1. megjegyzés átalakítása is.   2. feladat. Egy természetes szám hatodik hatványának számjegyei nagyság szerint rendezve a következők: $\begin{array}{c}{\displaystyle \mathrm{0,}\mathrm{2,}\mathrm{3,}\mathrm{4,}\mathrm{4,}\mathrm{7,}\mathrm{8,}\mathrm{8,}9.}\end{array}$ Mi ez a szám?   Megoldás. Ha létezik a feltételnek megfelelő $x$ szám, akkor az kétjegyű, mert a 7-jegyű ${10}^6$ számnál nagyobb, de a 13-jegyű ${100}^6$-nál kisebb a hatodik hatványa. Szűkebb korlátokat adnak $x^6$-ra az adott számjegyekkel írható legkisebb és legnagyobb szám. Mivel 0 az első helyen nem állhat, így azt nyerjük, hogy $\begin{array}{c}{\displaystyle 203447889\le x^6\le 988744320.}\end{array}$ A felső korlátot kissé növelve $\begin{array}{c}{\displaystyle x^6<{10}^9\mathrm{,}{x}^2<{10}^3\mathrm{,}x<\sqrt[]{1000}<32.}\end{array}$ Az alsó korlát minden esetre lényegesen nagyobb ${20}^6\left(=64000000\right)$-nál, viszont kisebb, mint ${25}^6={\left(625\right)}^3>{\left(600\right)}^3=216000000$. Továbbmenve ${24}^6={\left({\left(3\cdot 8\right)}^3\right)}^2={\left(27\cdot 512\right)}^2=13{824}^2<14{000}^2=196000000$ már kisebb, mint az alsó korlát. Így a keresett szám 24 és 32 közé eshet csak (a határokat nem engedve meg).1 Vegyük észre, hogy az $x^6$-ra megadott számjegyek összege osztható 3-mal, vagyis $x^6$ is osztható 3-mal. Ez csak úgy lehet, ha maga $x$ is 3-mal osztható (3-mal nem osztható szám semmilyen hatványa sem osztható 3-mal). A 24-nél nagyobb és 32-nél kisebb természetes számok közül csak a 27 és a 30 osztható 3-mal, de 30 nem lehet a feladat megoldása, mert hatodik hatványa 6 db 0-ra végződik. Viszont ${27}^6=387420489$, a jegyek megegyeznek az adottakkal, tehát $x=27$.   Megjegyzések. 1. A 3-mal való oszthatóság helyett a feladatnak megfelelő számot végződése alapján is kiválaszthatjuk. Ha ugyanis $x$ végződése rendre $\begin{array}{c}{\displaystyle \mathrm{0,}\mathrm{1,}\mathrm{2,}\mathrm{3,}\mathrm{4,}\mathrm{5,}\mathrm{6,}\mathrm{7,}\mathrm{8,}\mathrm{9,}}\end{array}$ akkor $x^6$ végződése rendre $\begin{array}{c}{\displaystyle \mathrm{0,}\mathrm{1,}\mathrm{4,}\mathrm{9,}\mathrm{6,}\mathrm{5,}\mathrm{6,}\mathrm{9,}\mathrm{4,}1.}\end{array}$ Mivel az adott számjegyek között 1, 5 és 6 nem szerepel, a már kiszámított korlátok közti számok közül $x$ csak 27, 28 vagy 30 lehet. 30 a már említett ok miatt nem felel meg, ${28}^6$ jegyei nem a megadottak, 27 viszont megfelel. 2. Több versenyző $x^6$-nak 9-cel való oszthatóságából $x$-nek 9-cel való oszthatóságára következtetett, és a kiszámított korlátok között egyedüli lehetőségként a 27-et jelölte meg. Ez a következtetés hamis, mert pl. $3^6$ osztható 9-cel, de maga az alap: 3 nem.   3. feladat. Jelölje $f$ az ,,$a$'' és $b$ félegyenesek alkotta szög felezőjét. Egy az ,,$a$'' és $f$ félegyeneseket érintő $k_1$ kör ,,$a$''-t az $A$ pontban, egy $a$ $b$ és $f$ félegyeneseket érintő $k_2$ kör $b$-t a $B$ pontban érinti. Igazoljuk, hogy az $AB$ egyenes a $k_1$ és $k_2$ körökből egyenlő húrokat metsz ki.   Megoldás. Az $a$ és $b$ félegyenesek közös kezdőpontját jelöljük $C$-vel, a két kör középpontját $O_1$-gyel és $O_2$-vel, e három pont vetületét az $AB$ egyenesen $T$-vel, $F_1$-gyel és $F_2$-vel. A vizsgálandó húrok egyenlősége helyett nyilván elegendő a felüknek, $A{F}_1$-nek és $B{F}_2$-nek az egyenlőségét kimutatni. 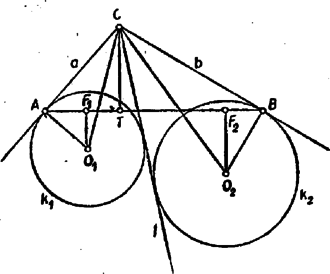    $\begin{array}{c}{\displaystyle \text{<span style="font-style: italic;">1. ábra</span>}}\end{array}$   Ha $O_1$ nem esik az $AB$ egyenesre (azaz $BAC\sphericalangle \ne {90}^{\circ }$), akkor az $A{O}_1{F}_1$ és a $CAT$ derékszögű háromszögekben az $A$-nál, illetőleg $C$-nél levő szögek merőleges szárú hegyes szögek, ezért egyenlők, s így a két háromszög hasonló, tehát megfelelő oldalaik aránya egyenlő: $\begin{array}{c}{\displaystyle A{F}_1:A{O}_1=CT:CA\mathrm{,}}\end{array}$ ebből $\begin{array}{c}{\displaystyle A{F}_1=\frac{A{O}_1}{CA}\cdot CT\mathrm{.}}\end{array}$ (1) Ugyanígy a $B{O}_2{F}_2$ és $CBT$ háromszögek hasonlósága alapján (hacsak $ABC\sphericalangle \ne {90}^{\circ }$) $\begin{array}{c}{\displaystyle B{F}_2=\frac{B{O}_2}{CB}\cdot CT\mathrm{.}}\end{array}$ (2) Az állítás igazolásához most már elegendő az $A{O}_1/CA$ és $B{O}_2/CB$ arányok egyenlőségét belátnunk. Ez viszont fennáll, mert tagjaik a $CA{O}_1$ és a $CB{O}_2$ derékszögű háromszögek befogói, e háromszögek pedig hasonlók, mert $C$-nél levő szögük az $a$ és $b$ félegyenesek hajlásszögének negyedrésze. Az ábrán az $ABC$ háromszög $A$-nál és $B$-nél levő szöge hegyesszög, meggondolásunk azonban akkor is helyes marad, ha valamelyik (pl. az $A$-nál levő) szög tompaszög. Abban az esetben viszont, ha pl. $CA{O}_1\sphericalangle \ne {90}^{\circ }$, az $AB$ egyenes átmegy $O_1$-en, a $T$ pont egybeesik $A$-val, íg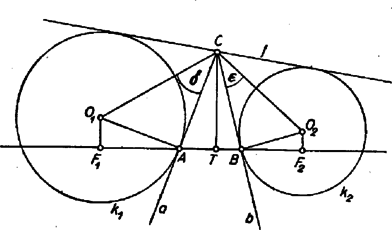y $\begin{array}{c}{\displaystyle A{F}_1=A{O}_1=\frac{A{O}_1}{CA}\cdot CA=\frac{A{O}_1}{CA}\cdot CT\mathrm{,}}\end{array}$ tehát az (1) összefüggés ebben az esetben is fennáll. A bizonyítás további része változatlanul alkalmazható ebben az esetben is.     $\begin{array}{c}{\displaystyle \text{<span style="font-style: italic;">2. ábra</span>}}\end{array}$   Megjegyzés. Az (1) és (2) összefüggések levezetésében nem használtuk ki, hogy $f$ szögfelező; ezek még akkor is fennállnak, ha $f$ az $a$ és $b$ határolta konkáv szögtérben van. (Ekkor a két kör érintési pontja $f$-en közrefogja $C$-t.) $A{O}_1/AC$, ill. $B{O}_2/BC$ általában azon szögek felének a tangense, amelyet $f$-nek $k_1$-et érintő félegyenese $a$-val, ill. $k_2$-t érintő félegyenese $b$-vel zár be. Ezeket a félszögeket $\delta$-val, ill. $\epsilon$-nal jelölve (1) és (2) alapján a két körből kimetszett húrok hosszának arányára (ismét a húrok felével számolva) $\begin{array}{c}{\displaystyle \frac{A{F}_1}{B{F}_2}=\frac{\text{tg <math xmlns="http://www.w3.org/1998/Math/MathML"><mi>δ</mi></math>}}{\text{tg <math xmlns="http://www.w3.org/1998/Math/MathML"><mi>ε</mi></math>}}\mathrm{.}}\end{array}$ Lukács Ottó, Scharnitzky Viktor, Surányi János 1Az $x^6$-ra nyert egyenlőtlenségpárból leggyorsabban logaritmus segítségével kaphatunk $x$-re korlátokat. Mivel kétjegyű korlátot keresünk, elég négy (sőt akár 3) értékes jegyet tartani meg a 9-jegyű számokból, persze az alsó korlátot közben lefelé, a felsőt fölfelé kerekítve.