| Cím: | A lineáris programozásról | ||
| Szerző(k): | Scharnitzky Viktor , Surányi János | ||
| Füzet: | 1962/november, 97 - 104. oldal |  PDF | MathML PDF | MathML |
|
| Témakör(ök): | Szakmai cikkek | ||
|
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. Gyakran olvassuk, hogy egy üzemben, építkezésnél vagy közlekedési vállalatnál a munka jobb megszervezése, felesleges szállítások megszüntetése útján minden befektetés nélkül megtakarítást értek el, néha nem is kicsit. Nyilvánvaló, hogy ezeket gondos vizsgálatok és számítások előzték meg. Felvetődik a kérdés, milyen matematikai módszerek segítségével lehet ilyen bonyolult kérdéseket egyáltalában matematikai formába önteni, majd megoldani? A legegyszerűbb, és éppen ezért a legelterjedtebben használt matematikai módszer, amely tervező és közgazdász szakemberek rendelkezésére áll ilyen problémák megoldására, a lineáris programozás. Ennek a köréből mutatunk be egy példát, amely középiskolai ismeretekkel is megoldható. 1. Egy gyakorlati feladat. Egy üzemrész kétféle terméket állít elő. A termékek 1‐1 darabjának előállításához szükséges munkaműveletek: az I. terméknél: 2 perc marás, 2 perc csiszolás, 5 perc festés, a II. terméknél: 2 perc préselés, 1 perc csiszolás, 5 perc festés. A szükséges gépek egy műszak alatt az alábbi időtartamokra vehetők igénybe: A feltételek ilyen megadása általában még a munka sokféle beosztását teszi lehetővé. A feladat általában az, hogy valamilyen célkitűzés (pl. egy időszak alatt gyártott érték, elért nyereség stb.) szempontjából a legkedvezőbb beosztást, más szóval munkaprogramot találjuk meg. Ehhez azonban hasznos, ha ismerjük az összes lehetséges munkaprogramot. Ezzel a feladattal foglalkozunk először. Feltételezzük, hogy a felhasználandó anyagok a szükséges mennyiségben állnak rendelkezésre. Meg kell keresnünk mindenek előtt azokat a matematikai összefüggéseket, amelyek együttesen pontosan leírják az adott feltételeket. (Ezeket szokás a probléma matematikai modelljének nevezni.) Készüljön egy műszak alatt az I. termékből A feltételek matematikai modellje tehát egy kétismeretlenes egyenlőtlenségrendszer. Az üzemrész annyiféle termelési programot készíthet a két termék gyártására, ahány e négy korlátnak, illetve egyenlőtlenségnek eleget tevő számpárt tudunk az Az egyenlőtlenségrendszert derékszögű koordinátarendszerben ábrázolva, grafikus úton fogjuk megoldani. 2. Kétismeretlenes elsőfokú egyenlőtlenség rendszerek grafikus megoldása. Az Hasonlóan a feladat első egyenlőtlenségének, amely A második egyenlőtlenséget 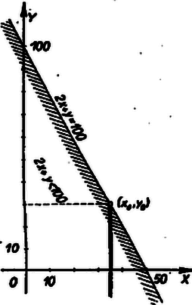 Vizsgáljuk most a csiszológép szolgáltatta
A negyedik egyenlőtlenség így írható: Ezzel a feladatban szereplő egyes egyenlőtlenségek geometriai tartalmát külön‐külön megállapítottuk. Mielőtt eredményeinket összegezzük, nézzünk még egy példát kétismeretlenes elsőfokú egyenlőtlenség ábrázolására, hogy a negatív együttható szerepét is lássuk. 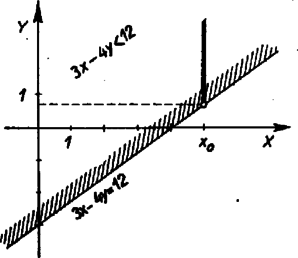 Keressük pl. a
A (3)-nak eleget tevő A fentiekben látott módon minden kétismeretlenes elsőfokú egyenlőtlenség geometriai jelentését meg tudjuk állapítani. Térjünk ezután vissza eredeti feladatunk megoldásához. 3. A célszerű munkaprogramok megkeresése. Az 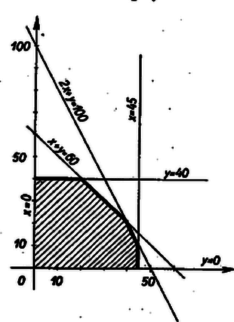 Ezzel sem válik azonban a munkaprogram egyértelművé, mert a) Vizsgáljuk meg először azt, milyen program mellett lesz a termelési érték maximális. A mondott feltételek mellett egy bizonyos 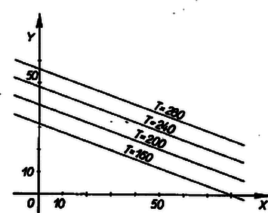 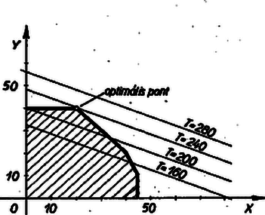 A 4. ábrát 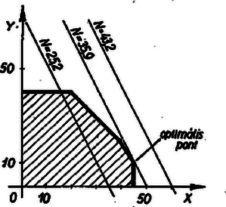 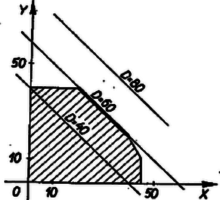 b) Milyen programot kell készítenünk, ha a maximális nyereség a cél? Egy adott c) Keressük meg azt a programot, amely a maximális darabszámot biztosítja. Az előzőekhez hasonlóan most a különböző Foglaljuk táblázatba eddigi eredményeinket: A tervezés során természetesen sok más szempont is felmerülhet (önköltség, energiafelhasználás stb.). Ezek alapján tovább lehetne bővíteni ezt a táblázatot. De már az eddigi eredmények is választ adnak néhány, a termelés megszervezése szempontjából fontos kérdésre. A táblázat megmutatja a különféle optimális pontokat ‐ ha ilyenek vannak ‐, vagy optimális határokat ‐ példánkban a c) eset ‐, amelyeken belül, esetleg még más szempontokat is figyelembe véve, a szervezők a legmegfelelőbb programot választhatják ki. Esetünkben pl. a maximális termelési értéket és a maximális darabszámot egyszerre is elérheti az üzemrész, ha az I. termékből 20, a II-ból pedig 40 darabot termel. Az ábrákról az is megállapítható, hogy adott esetben meddig lehet észszerű engedményt tenni valamely szempont szerinti optimális program rovására. Leolvasható pl., hogy ha a maximális termelési érték elérése a cél, akkor csak a présgép és a festőműhely kapacitását használjuk ki teljesen, mert ez az optimális pont éppen a présgép és a festőműhely miatti korlátozást ábrázoló egyenesek metszéspontja. Ekkor a többi gép bizonyos ideig állni kénytelen. Viszont ha a maximális nyereség elérésére törekszünk, a marógép és a csiszológép dolgozik teljes kapacitással és a többi számára tervezhetünk más munkát is. 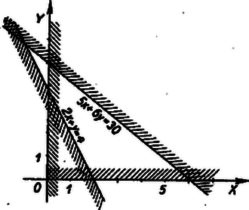 4. Megjegyzés. A tárgyalt feladatban láttuk, hogy bizonyos szempont szerint (termelési érték, nyereség) egyetlen optimális program létezik, más szempont szerint (darabszám) több (végtelen sok) optimális program is lehetséges. Előfordulhat azonban természetesen az az eset is, hogy a feladat egyáltalában nem oldható meg, mert a feltételi egyenlőtlenségek ellentmondanak egymásnak. Ilyen p1. az alábbi egyenlőtlenségrendszer: 5. A lineáris programozás feladata általában. A föntiekben egy nagyon egyszerű példával igyekeztünk illusztrálni a lineáris programozást. Általában egy üzem munkáját nem két, hanem sokkal több adattal lehet leírni. Ezek megválasztására a termelés külső feltételei (a fenti példában a gépek kapacitása) általában csak tág feltételeket szabnak. A feladat ezek közt a feltételek közt olyan munkaprogramot találni, amely mellett valamilyen, a termelést leíró adatoktól függő mennyiség a lehető legnagyobb vagy a lehető legkisebb lesz. A termelési feltételek adta korlátozásokat általában egyenlőtlenségekkel lehet leírni, és azt kell megállapítanunk, hogy egy további megadott függvény az egyenlőtlenségrendszert kielégítő értékrendszerek közül melyikre vagy melyekre veszi fel a legnagyobb, vagy melyikre a legkisebb értéket. A tárgyalt példát két körülmény tette egyszerűvé, az, hogy a változóknak csak elsőfokú kifejezései léptek fel és hogy csak két változó szerepelt. Az, hogy csak elsőfokú (latin szakkifejezéssel lineáris) kifejezések lépnek fel, azt eredményezi, hogy számítások közben csak a négy alapműveletre van szükség. Az ilyen számítások igen könnyen végezhetők gépekkel. Ezeknek a fontosságát növeli az is, hogy a gyakorlati problémáknál igen gyakran lépnek fel egyenes arányosságban levő mennyiségek (tehát elsőfokú kifejezéssel jellemezhető összefüggések), vagy legalábbis jó közelítésben arányosnak tekinthetők. Az ilyen esetekkel foglalkozik a lineáris programozás. Általánosan tehát így fogalmazható a probléma: valamilyen egyenlőtlenségeknek, és kérdezzük, hogy ezen feltételek mellett egy A két változó annyiban jelentett könnyebbséget, hogy a matematikai feladatot geometriailag tudtuk szemléltetni, és egyenesek húzásával, főleg pedig egyenesek párhuzamos elmozgatásával megoldani. Ez a lehetőség elvben 3 változó esetén a térben még rendelkezésre áll (bár gyakorlatban nehéz megvalósítani), több változó esetén azonban a geometriai szemléltetést nem tudjuk felhasználni. Ilyen esetben ‐ és a gyakorlatban ez fordul elő a legtöbbször ‐ algebrai jellegű megoldást kell keresnünk. Többféle ilyen megoldási módszer is ismeretes. Bár ezek elvileg mind elemiek, azonban nagy mennyiségű számítást igényelnek.3 6. A szállítási probléma. A lineáris programozás körébe tartozó egyik jellegzetes feladattípus az ún. szállítási probléma. Bizonyos anyagot több ismert telephely használ fel és több gyár állít elő (p1. téglát építkezéshez). Ismerjük az egyes gyárak termelési kapacitását, az egyes telephelyek igényét, és ismerjük a szállítási költségeket, amelyek különböző gyárak és telephelyek között különbözők lehetnek (pl. más szállítási eszközök, terepviszonyok, egyéb miatt). Találomra kialakult megoldásnál előfordul az is, hogy két távoli felvevőhely kölcsönösen a másikhoz közeli gyárból szállít (keresztszállítás). Az ilyeneket könnyű megszüntetni, a leggazdaságosabb megoldást azonban találgatás útján nem lehet megtalálni. A lineáris programozás módszereivel megkereshető a szállítások olyan elosztása, amely mellett a szállítási költség minimális. Ha a felvevőhelyek igényének összege egyenlő a gyárak együttes termelésével, akkor a feltételeket ‐ az előző feladattól eltérően ‐ nem egyenlőtlenségek, hanem egyenletek segítségével írhatjuk fel. Ezen feltételi egyenletrendszer általában több ismeretlent tartalmaz, mint egyenletet, ennek teljesülése mellett keressük a költségek minimumát. Az optimális megoldás meghatározása és gyakorlati megvalósítása ilyen feladatoknál néhány esetben váratlanul nagy mérvű megtakarítást tett lehetővé. 7. Történeti megjegyzések. Közgazdasági problémák megoldására matematikai módszerek alkalmazását már két évszázaddal ezelőtt elkezdték, de az első, gyakorlatilag is jól használható eredmények csak a XX. század első harmadában váltak ismeretessé. Ezek W. W. Leontiff orosz, valamint Neumann János magyar származású amerikai matematikusok nevéhez fűződnek. Az egyre magasabb fokú szervezettséget követelő ipari fejlődés nyomán mind a Szovjetunióban, mind a kapitalista államokban (főleg az Egyesült Államokban) a második világháború előtt és alatt csaknem egy időben jelentek meg a lineáris programozás alkalmazásait bemutató, majd a második világháború után a lineáris programozás elméletét megalapozó és továbbfejlesztő munkák. Az első olyan mű, amely lineáris programozással old meg feladatokat, L. V. Kantorovics szovjet matematikus 1939-ben megjelent cikke. Vele csaknem egy időben, 1941-ben F. L. Hitchook amerikai matematikus közölt egy megoldást a szállítási problémára. Megemlítjük, hogy a szállítási probléma egy másik megoldása, az ún. ,,magyar módszer'' Kőnig Dénes, Egerváry Jenő magyar és H. W. Kuhn amerikai matematikusok nevéhez fűződik. A lineáris programozási feladatok megoldására szolgáló egy általános módszer, az ún. szimplex módszer, 1947-ben alakult ki G. B. Dantzig amerikai matematikus munkássága nyomán. Azóta már több olyan módszert is kidolgoztak, amely nem csupa elsőfokú összefüggés esetén is alkalmazható. Scharnitzky Viktor, Surányi János 1Az olvasóra bízzuk annak átgondolását, hogy ez akkor is helyes, ha a nagyobb oldalon pozitív szám áll. (A kisebb oldalon ez esetben állhat pozitív szám is, negatív is.)2Célszerű volt két indexes jelölést használni ( |