Cím: 1961. évi Kürschák József matematikai tanulóverseny feladatainak megoldása
Szerző(k):  Hajós György 
Füzet: 1962/március, 98 - 107. oldal  PDF  |  MathML 
Témakör(ök): Kürschák József (korábban Eötvös Loránd)

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Első feladat. A sík négy pontja hat távolságot határoz meg. Bizonyítsuk be, hogy e távolságok legnagyobbika a legkisebbel osztva nem adhat 2-nél kisebb hányadost.

 
I. megoldás. Legyen P1, P2, P3, P4 a sík szóban forgó négy pontja. Válasszuk hosszegységül az általuk meghatározott távolságok legkisebbikét. Azt kell tehát bebizonyítanunk, hogy a hat távolság között van legalább 2 hosszúságú.
Legyen P1 és P2 egymástól minimális, tehát egységnyi távolságra. Írjunk köréjük egy-egy egységsugarú kört (1. ábra). A P3, P4 pontok egyike sem lehet e körök valamelyikén belül, mert akkor P1P2 nem volna minimális. Írjunk most P1 és P2 köré 2 sugárral egy-egy kört. Ezek a P1P2BA négyzet B, ill. A csúcsán haladnak át. Ha a P3, P4 pontok valamelyike nincs a két most rajzolt kör valamelyikén belül, akkor a kör középpontjától legalább 2 távolságra van.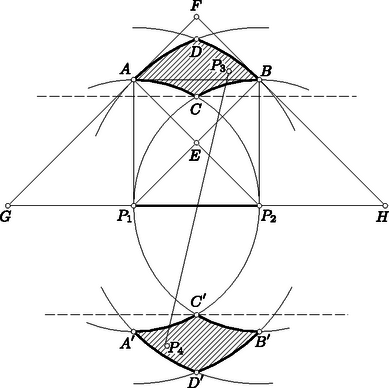
 

 

1. ábra

 

Ezek szerint csak azzal az esettel kell foglalkoznunk, amikor P3 is és P4 is az utóbb rajzolt körök mindegyikén belül helyezkedik el, de egyikük sincs az előbb rajzolt körök valamelyikének a belsejében. Ez azt jelenti, hogy P3 és P4 ábránk körívekkel határolt, vonalkázott tartományaiban van, de a tartományok határvonalából az AD, DB ívek, valamint az A'D', D'B' ívek pontjait nem számítjuk a tartományokhoz.
Ábránkból kiolvashatjuk, hogy az ACBD ívnégyszög az AB átlójú négyzetben helyezkedik el, s hogy az ívnégyszög pontjai közül csak A és B van a négyzet határvonalán (lásd az alábbi megjegyzést). Ebből a szimmetria miatt mindkét tartományunkra következik, hogy egy tartomány bármely két pontjának távolsága 1-nél kisebb, hiszen egy négyzetben elhelyezkedő szakasz, ha a négyzetnek nem átlója, akkor az átlónál rövidebb. Még nyilvánvalóbb ez a tény, ha arra gondolunk, hogy a négyzet köré írt kör átmérője a négyzet átlója, s hogy a körlemezen elhelyezkedő szakasz, ha nem átmérő, akkor az átmérőnél rövidebb.
Arra az esetre szorítkozhatunk tehát, amikor P3 és P4 más-más vonalkázott tartományhoz tartozik. A C, C' pontokon át párhuzamosokat húzunk a P1P2 szakasszal. E párhuzamosok által határolt sáv elválasztja a két vonalkázott tartományt, és szélessége 2-nél nagyobb, hiszen a CP1 és P1C' egységnyi szakaszok szöge 120∘, azaz nagyobb, mint 90∘. A P3P4 szakasz ezek szerint átvágja az említett sávot, s hossza ezért legalább akkora, mint a sáv szélessége, tehát 2-nél nagyobb.
 
Megjegyzés. Az ábrából olvastuk ki azt, hogy az AB átlójú négyzet tartalmazza az ACBD ívnégyszöget, s hogy az ívnégyszög pontjai közül csak A és B van a négyzet határán. Ezt itt szigorúbban be is bizonyítjuk.
Nyilvánvaló, hogy az A, B pontok az ívnégyszöghöz tartoznak. Elég tehát azt bizonyítanunk, hogy az ívnégyszögnek nincs más pontja a négyzet határán. Nyilvánvaló, hogy az AF, BF egyeneseken nincs az ívnégyszögnek további pontja, hiszen ezek az egyenesek az ívnégyszöget tartalmazó köröket az A, ill. B pontban érintik. Ebből az is következik, hogy ívnégyszögünk az FGH△-ben helyezkedik el. A P1 középpontú kör AP2 íve kettévágja ezt a háromszöget, és elválasztja az ívnégyszöget az AP2 húrtól. Közös pontjuk csak a húr végpontja lehet. Ezért az ívnégyszögnek nincs az AE szakaszon elhelyezkedő, A-tól különböző pontja. Hasonló indokolással nincs a BE szakaszon elhelyezkedő, B-től különböző pontja sem.
 
II. megoldás. Ha a derékszögű háromszög átfogóját a kisebbik (pontosabban: a másiknál nem nagyobb) befogóval elosztjuk, 2-nél nem kisebb hányadoshoz jutunk. Ez abból következik, hogy a≤b esetén c2=a2+b2≥2a2, tehát c/a≥2.
Ha a háromszög két oldalát változatlanul hagyjuk, de az általuk közrefogott szöget növeljük, akkor a harmadik oldal is növekszik. Ezért tompaszögű háromszögre, sőt (egy egyenesen elhelyezkedő, csatlakozó szakaszokká) elfajuló háromszögre is kimondhatjuk, hogy legnagyobb oldala a legkisebbel osztva legalább 2 értékű hányadost ad.
Elég ezért azt bizonyítanunk, hogy a sík bármely négy pontja között van három olyan, amely derékszögű, tompaszögű vagy elfajuló háromszöget határoz meg. Induljunk ki a sík négy pontjából. Feltehetjük, hogy nincs közöttük három egy egyenesen elhelyezkedő. Tekintsük a négy pont konvex burkát, azaz azt az idomot, amelyet úgy kapunk, hogy a pontok köré fonalat feszítünk. Minthogy a pontok nincsenek mindannyian egy egyenesen, konvex burkuk vagy háromszög, vagy négyszög.
Ha a P1P2P3△-höz jutunk (2. ábra), akkor P4 ennek belsejében van, hiszen három pont nem lehet egy egyenesen. A P4P1, P4P2, P4P3 szakaszok háromszögünket három háromszögre vágják fel. Ezeknek P4-nél elhelyezkedő három szöge együttesen 360∘, s ezért közöttük tompaszög is van (sőt közülük legalább kettő tompa). Egy ilyen tompaszög a pontjainkból alakított tompaszögű háromszög szöge.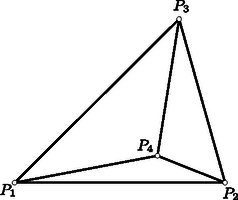
 

 

2. ábra

 

Ha a konvex burok négyszög, akkor ennek a szögeiről elmondhatjuk, hogy nem lehet mindegyik hegyes, hiszen az összegük 360∘. A legnagyobb szög tehát derékszög vagy tompaszög, s ez egy a pontjainkból alakított derékszögű vagy tompaszögű háromszög szöge.
 
Megjegyzések. 1. A feladat állításánál valamivel többet is kimondhatunk. Nemcsak az igaz, hogy a vizsgált hányados nem lehet 2-nél kisebb, hanem az is, hogy 2 a legkisebb olyan szám, amelyre ez igaz. Ezt a négyzet négy csúcsa bizonyítja, hiszen belőlük 2 adódik hányadosul.
Még azzal is kiegészíthetjük a mondottakat, hogy 2 csak egy négyzet csúcsai esetében lép fel hányadosként. Ez mindkét megoldásunkból könnyen kiolvasható.
 
2. Felmerül a kérdés, hogy ha a síknak nem négy, hanem n>2 pontjából indulunk ki, akkor az általuk meghatározott távolságok legnagyobbikát a legkisebbel osztva mekkora hányadoshoz juthatunk. Ez a hányados természetesen tetszőlegesen nagy lehet. Kérdésünk az, hogy mi a hányados lehetséges legkisebb értéke. Azt is kérdezhetjük, hogy a lehetséges legkisebb érték a pontok milyen elhelyezkedése esetén lép fel.
Az n=3 esetben nyilvánvaló, hogy 1 a minimum, s hogy ezt csak a szabályos háromszög csúcsai szolgáltatják. Feladatunk az n=4 esetről szólt. Második megoldásunk módszerével könnyű bebizonyítani, hogy ha n=5, akkor a minimumot a szabályos ötszög csúcsai szolgáltatják, tehát a minimum értéke 12(5+1)≈1,618, s hogy ez más esetben nem lép fel. Ezt a bizonyítást Bollobás Béla a versenydolgozatában el is végezte.
Az n>5 esetekben nem ismeretes a válasz. Megemlítendő mindenesetre, hogy már az n=6 esetben sem adja a szabályos sokszög a minimális értéket, hiszen a szabályos hatszög minden második csúcsát ,,benyomva'' a vizsgált hányados csökken, amit nem nehéz bebizonyítani.
 
3. Még nehezebb a kérdés, ha nem a sík, hanem a tér pontjaira vetjük fel. Itt természetesen csak az n>4 esetekre gondolunk. Már az n=5 eset elintézése sem könnyű. Bizonyítás nélkül megemlítjük, hogy ekkor a minimumot szolgáltató öt pontot úgy kell felvenni, hogy közülük három egy szabályos háromszöget határozzon meg, a másik kettő a háromszög síkjára szimmetrikusan, a háromszög síkjára a háromszög középpontjában emelt merőlegesen helyezkedjék el, és távolságuk a háromszög oldalával legyen egyenlő. A minimum értékére 12/7≈1,309 adódik. Említést érdemel, hogy ez a síkban négy pontra adódó értéknél kisebb.
 
4. A feladatnak még egy más irányú általánosítását is megemlítjük. A sík négy pontjából indulunk ki. Az általuk meghatározott hat távolságot nagyság szerint rendezzük: a legnagyobbal kezdjük, a legkisebbel végezzük, s közben természetesen ismétlődést is megengedünk. Ha e sorozat i-edik elemét a k-adikkal elosztjuk, a q(i,k)-val jelölt hányadoshoz jutunk. Azt kérdezzük, hogy megadott i<k értékekre ez a hányados milyen értékeket vehet fel. Ez a kérdés i és k különféle megválasztásának megfelelően 15 különböző kérdést tartalmaz. Feladatunk csak q(1,6) értékével foglalkozott, és q(1,6)≥2 bizonyítását kívánta. Első megjegyzésünk rámutatott, hogy q(1,6) felveheti a 2 értéket is. Könnyű belátni, hogy minden nagyobb értéket is felvehet. A q(1,6)-ra felvetett kérdésre tehát azt kell felelnünk, hogy q(1,6) értéke lehet minden olyan szám, amely 2-nél nem kisebb.
A többi 14 kérdés vizsgálatát az olvasóra hagyjuk. Különösebb nehézséget egyikük megválaszolása sem jelent, de vigyázni kell, mert a felelet nem minden kérdésre ugyanaz.
Hasonló kérdést vethetünk fel a sík n pontjára, vagy a tér n pontjára is. Így már nehéz kérdésekhez is eljutunk, és csak nagyon kevés rájuk vonatkozó ismert választ említhetnénk. Megemlítjük, hogy a sík 3n pontjára vonatkozólag q(1,3n2+1)≥2. Ezt Turán Pál és Erdős Pál bizonyította be. Bizonyításuk többek között éppen feladatunk állítására támaszkodik. Maga a feladat is innen ered.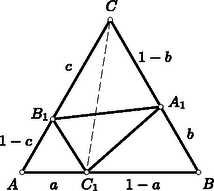
 
Második feladat. Bebizonyítandó, hagy az 1-nél kisebb, pozitív a, b, c számokból képezett
(1-a)b,(1-b)c,(1-c)a
szorzatok nem lehetnek mindannyian 14-nél nagyobbak.
 
I. megoldás. Abból indulunk ki, hogy ha 0<a<1, akkor
a(1-a)≤14,
hiszen ez átrendezéssel keletkezik a nyilván helyes (a-12)2≥0 egyenlőtlenségből. Ebből (és a b, c számokra felírt hasonló egyenlőtlenségekből) következik, hogy a feladatunkban szereplő három szorzat szorzata
(1-a)b⋅(1-b)c⋅(1-c)a=a(1-a)⋅b(1-b)⋅c(1-c)≤(14)3.
Mind a három vizsgált szorzat tehát nem lehet 14 -nél nagyobb, mert akkor a szorzatuk (14)3-nél nagyobb volna.
 
II. megoldás. A vizsgált három szorzat értékhármasa nem változik meg, ha az a, b, c számokat ciklikusan felcseréljük (azaz a b, c, a vagy a c, a, b sorrendre térünk át). Feltehetjük ezért, hogy a három szám közül a a legnagyobb, hogy tehát b≤a. Ebből következik, hogy
(1-a)b≤(1-a)a≤14.
Az utolsó lépés felhasználta azt az egyenlőtlenséget, amelyből az első megoldás kiindult.
 
III. megoldás. Egy egységoldalú szabályos ABC△ három csúcsából felmérjük a háromszög más-más oldalára az a, b, c távolságokat. A végpontok az A1B1C1△-et határozzák meg (3. ábra). Ezt a háromszöget az eredetivé három háromszög egészíti ki. Ezek területe az eredeti háromszög területének rendre (1-a)b, (1-b)c és (1-c)a-szorosa, hiszen az ABC△-ből pl. az AB alapot (1-a)-szorosára csökkentve a C1BC△-höz, s ennek magasságát b-szeresére csökkentve a C1BA1△-höz jutunk.
 

 

3. ábra

 

Elég tehát megmutatnunk, hogy ha egy egységterületű szabályos háromszögbe háromszöget írunk, akkor a keletkező három kiegészítő háromszög között van 14-nél nem nagyobb területű. A középvonalak határolta A2B2C2△-ről és az ezt kiegészítő háromszögekről tudjuk, hogy területük 14. Állításunk nyilvánvalóan helyes tehát akkor, ha a most említett háromszögek valamelyike tartalmazza beírt A1B1C1△-ünk kiegészítő háromszögeinek valamelyikét. Feltehetjük ezért, hogy a középvonalak szétválasztják a rendre a BC, CA, AB oldalakon elhelyezkedő A1, B1, C1 pontokat (4. ábra), mégpedig válassza el a C2A2, A2B2, B2C2 középvonal rendre az A1, B1, C1 pontot a másik kettőtől. Ennek az elhelyezkedésnek arra a következményére fogunk támaszkodni, hogy az A1B1 egyenes metszi az AB félegyenest, s hogy a C2A1 egyenes metszi a CA félegyenest. Elegendő most már csak azt bizonyítanunk, hogy az A1B1C1△ területe 14-nél nagyobb. Ebből következik ugyanis, hogy kiegészítő háromszögeinek területösszege 34-nél kisebb, hogy tehát van közöttük 14-nél kisebb területű.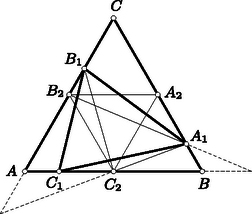
 

 

4. ábra

 

Az A1B1C1△ területét csökkentjük, ha C1 csúcsát C2-be toljuk el. Ez abból következik, hogy C1 az eltoláskor közeledik az A1B1 egyeneshez, hiszen közeledik az AB és az A1B1 egyenesek metszéspontjához. Az A1B1C2△ területe tovább csökken, ha B1 csúcsát B2-be toljuk el, mert ekkor B1 az AC, C1A2 egyenesek metszéspontjához, tehát az A1C2 egyeneshez is közeledik. Ha a kapott A1B2C2△ A1 csúcsát a B2C2 oldallal párhuzamosan A2-be toljuk el, területe nem változik meg. Minthogy területcsökkentéssel az 14 területű A2B2C2△-höz jutottunk, az A1B1C1△ területe 14-nél valóban nagyobb.
 
Megjegyzések. 1. A feladatot megoldó versenyzők nagy többsége az első megoldást találta meg. A második megoldás mondható a legegyszerűbbnek. A harmadik megoldás lényegesen bonyolultabb, viszont rámutat arra a geometriai háttérre, amelyből a feladat származott.
 
2. Feladatunk az a, b, c számokra vonatkozó két megszorítást tartalmaz: megköveteli egyrészt, hogy ezek a számok 1-nél kisebbek, másrészt azt is, hogy pozitívak legyenek. Egyik megszorításra sincs szükség, de valamelyikre szükség van.
Ha ugyanis csak azt követeljük meg, hogy a számok 1-nél kisebbek legyenek, akkor 1-a, 1-b, 1-c pozitív értékek, s az esetleg előforduló negatív vagy 0 értékű b, c, a számmal szorozva 14-nél kisebb szorzatot adnak. Ha viszont csak a, b, c pozitivitásához ragaszkodunk, akkor ezeket az esetleg előforduló negatív vagy 0 értékű 1-c, 1-a, 1-b értékekkel szorozva jutunk 14-nél kisebb eredményhez. A feladat állítása ezek szerint mindkét esetben csak érdektelen tartalommal bővül. A két bővítés egymástól lényegében nem is különbözik, hiszen a feladat változatlan marad, ha benne a, b, c helyébe rendre az 1-c, 1-b, 1-a értékeket írjuk. Az a=12, b=2, c=-1 példa mutatja, hogy mind a két követelést nem hagyhatjuk el.
 
3. Első két megoldásunk módszerével (az előző megjegyzésre is támaszkodva) könnyedén bebizonyíthatjuk, hogy ha az a1,a2,...,an, számok pozitívak, akkor az
(1-a1)a2,(1-a2)a3,...,(1-an)a1
szorzatok nem lehetnek mindannyian 14-nél nagyobbak, sőt feladatunk még messzebb menő általánosításaként azt is, hogy ha a pozitív a1,a2,...,an számoknak egy permutációja b1,b2,...,bn, akkor az
(1-a1)b1,(1-a2)b2,...,(1-an)bn
számok sem lehetnek mindannyian 14-nél nagyobbak.
 
4. Feladatunk annak bizonyítását kívánta meg, hogy három szám legkisebbike 14-nél nem nagyobb. Kérdezhetjük, hogy ha ezt a három számot nagyság szerint rendezzük, mit mondhatunk ki a középsőről és a legnagyobbról. Könnyű belátni, hogy (0 és 1 közötti számok körében maradva) a középső nem lehet 12-nél nagyobb, s hogy további korlátozás a három szám egyikére sem mondható ki.
Ha az előző megjegyzés általánosításainak a körében vetjük fel a hasonló problémát, kérdezve, hogy a nagyság szerint rendezett szorzatok közül az i-edikre milyen korlátozásnak kell teljesülnie (i=1,2,...,n), akkor már nehezebb problémákhoz jutunk.
 
Harmadik feladat. Tekintsünk két egymáson kívül elhelyezkedő kört, egy közös külső és egy közös belső érintőjüket. Érintési pontjaik mindkét körben egy-egy húrt határoznak meg. Bizonyítsuk be, hogy e húrok egyenesei egymást a középpontokat összekötő egyenesen metszik.
 
I. megoldás. Az O1, O2 középpontú körök A1A2 külső és B1B2 belső érintőjének metszéspontját C-vel jelöljük (5. ábra). Az O1A1CB1 és CA2O2B2 derékszögű deltoidok egymáshoz hasonlók, hiszen C-nél elhelyezkedő szögeik mellékszögek, s ebből következik, hogy szögeik páronként egyenlők. Deltoidok körében ez a hasonlóságot valóban biztosítja. A deltoidok CO1, CO2 átlói merőlegesek egymásra, mert az említett mellékszögek szögfelezői. Minthogy az A1B1, A2B2 átlók mindegyike merőleges a CO1, CO2 átlók egyikére (az ugyanazon deltoidbeli átlóra), mindegyikük párhuzamos a másikkal.
Messék az A1B1, A2B2 egyenesek az O1O2 centrálist a P1, P2 pontokban. Bebizonyítjuk, hogy ez a két pont azonos, hogy tehát az A1B1, A2B2 egyenesek metszéspontja valóban a centrálison van. Az 5. ábra szándékosan torz, hogy rajta okoskodásunkat jobban követhessük. Elmondhatjuk, hogy a következőkben ábránk torz voltát bizonyítjuk be.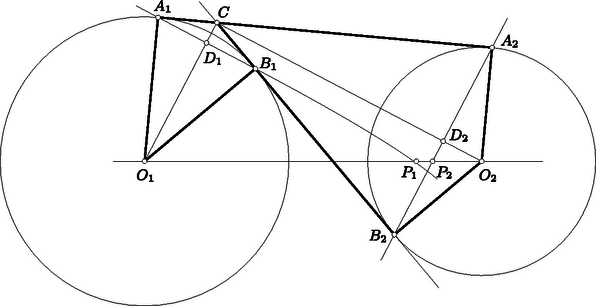
 

 

5. ábra

 

A deltoidok hasonlóságából következik, hogy átlóik D1, D2 metszéspontjára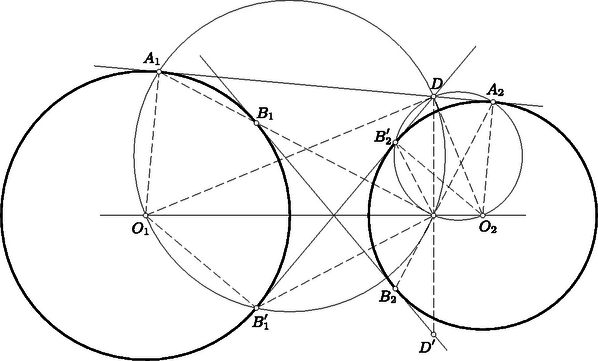
O1D1:O1C=CD2:CO2.
A párhuzamos szelők tétele szerint a CO1O2∢ szárait metsző A1B1, CO2 párhuzamosokra
O1D1:O1C=O1P1:O1O2,
és a CO2O1∢ szárait metsző A2B2, CO1 párhuzamosokra
CD2:CO2=O1P2:O1O2.
Aránypárjaink egybevetéséből következik, hogy
O1P1:O1O2=O1P2:O1O2,
hogy tehát O1P1=O1P2, azaz P1 és P2 egymással azonos pontok.
 
II. megoldás. A feladatban előforduló két érintőn kívül a másik B'1B'2 érintőt is meghúzzuk. Ez az A1A2 külső érintőt a D pontban metszi, D-nek a centrálisra vetett vetületét M-mel, a centrálisra vonatkozó tükörképét pedig D'-vel jelöljük (6. ábra).
 

 

6. ábra

 

Bebizonyítjuk, hogy M rajta van az A1B1, A2B2 egyenesek mindegyikén, és ezzel a feladat állítását igazoljuk.
Az O2D átmérőjű kör tartalmazza az A2, B'2, M pontokat, mert az O2D szakasz ezekből a pontokból derékszögben látható. Minthogy A2O2D∢=DO2B2'∢, a kerületi szögek tétele szerint A2MD∢=DMB'2∢. Ebből a szimmetria révén A2MD∢=D'MB2∢ következik, tehát az is, hogy az A2, M, B2 pontok egy egyenesen vannak.
Hasonlóan okoskodhatunk a másik esetben is. Az O1D átmérőjű kör tartalmazza az A1, B'1, M pontokat, mert az O1D szakasz ezekből derékszögben látszik. Minthogy A1DO1∢=O1DB'1∢, a kerületi szögek tétele szerint A1MO1∢=O1MB'1∢. Ebből a szimmetria révén következik, hogy A1MO1∢=B1MO1∢, hogy tehát az A1, B1, M pontok egy egyenesen vannak.
 

III. megoldás. Felhasználjuk azt, hogy ha két kör külső és belső érintőjének metszéspontját az egyik érintőn a hozzá legközelebb eső érintési ponttal összekötjük, mindig ugyanakkora szakaszhoz jutunk, bármely érintőpár metszéspontjából indultunk is ki. A 7. ábrán tehát 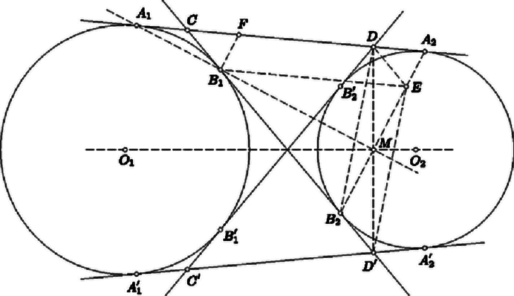CB1=DA2=D'B2.
 
 
7. ábra
 

Abból indulunk ki, hogy az A1B1, A2B2 egyenesek egymásra merőlegesek. Ezt az első megoldás mintájára láthatjuk be. Az egyenlőszárú A2B2C△-ből az A2C szárral párhuzamos EB1 szelő egy ugyancsak egyenlőszárú EB2B1△-et vág le. Ennek alapja az A2B2 egyenesen, magassága pedig az alapra merőleges A1B1 egyenesen helyezkedik el. Ezeknek az egyeneseknek az M metszéspontja felezi tehát az EB2 szakaszt.
Az egyenlőszárú A2B2C△-ből egy az alapjával párhuzamos egyenes az ugyancsak egyenlőszárú FB1C△-et vágja le. Ennek száraira a megoldás elején mondottak szerint FC=B1C=A2D. Ha tehát ezt a háromszöget az A1A2 egyenes mentén eltoljuk, az A2ED△-höz jutunk. Ezért ED párhuzamos és egyenlő a B1C szakasszal, tehát a D'B2 szakasszal is. Ebből következik, hogy az EDB2D' négyszög parallelogramma, hogy tehát EB2 és DD' átlója egymást felezi, azaz M felezi a DD' szakaszt is. Minthogy a D, D' pontok a centrálisra vonatkozólag egymás tükörképei, összekötő szakaszuk M felezőpontja a centrálison van. (Ezt a megoldást a versenyen Máté Attila találta, de csak hiányosan dolgozta ki.)
IV. megoldás. A hatványvonalra vonatkozó ismeretekből felhasználjuk azt, hogy mindazok a pontok, amelyekből két egymást metsző körhöz húzott érintőszakaszok egymással egyenlők, a körök közös húrjának az egyenesén vannak.
 
 
8. ábra

Ismét abból indulunk ki, amit már az első megoldásban beláttunk, hogy az A1B1, A2B2 egyenesek egymást az M pontban merőlegesen metszik. Thales tétele szerint tehát M hozzátartozik az A1A2 átmérőjű körhöz és a B1B2 átmérőjű körhöz is (8. ábra).
Az O1 pontból e két körhöz vont érintőkre O1A1=O1B1, s az O2 pontból hozzájuk vont érintőkre O2A2=O2B2. Az előrebocsátottak szerint tehát O1 és O2 egy olyan egyenesen van, amely a körök közös M pontját tartalmazza.
Ez azt bizonyítja, hogy az O1, O2, M pontok egy egyenesen vannak.
 
 Hajós György