Cím: Az 1961. évi Arany Dániel tanulóversenyek II. fordulóján kitűzött feladatok megoldása: A kezdők versenye
Szerző(k):  Varga Tamás 
Füzet: 1962/január, 5 - 8. oldal  PDF  |  MathML 
Témakör(ök): Arany Dániel

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

1. feladat. Bizonyítsuk be, hogy minden többjegyű négyzetszámban van legalább két különböző számjegy.

 
I. megoldás. A bizonyítandó állítást így is fogalmazhatjuk: nincs olyan többjegyű négyzetszám, amelynek minden jegye megegyezik.
Megjegyezzük, hogy ha egy szám elé nullákat írunk, értéke nem változik, de ezeket a nullákat a jegyek számának megállapításakor nem vesszük tekintetbe. Pl. 05 nem kétjegyű, hanem egyjegyű szám. Így a több 0-val írt 000...0 számok teljes négyzetek, de ezeket nem tekintjük többjegyűnek.
Ezek után a következő alakú számokról kell bebizonyítanunk, hogy nem lehet köztük négyzetszám:
1...1,4...4,7...7,2...2,5...5,8...8,3...3,6...6,9...9,
akárhány ‐ a szélsőkkel megegyező ‐ jegyet képzeljünk is a pontok helyére. (Az ,,akárhány'' szó itt nullát is jelenthet, vagyis azt, hogy a pontokat kihagyva a két szélső számjegyből alkotunk számot.) Közülük négyet mindjárt kizárhatunk, mert 2-re, 3-ra, 7-re és 8-ra nem végződhet négyzetszám. Az egyjegyű számok négyzetéről ezt a lehetséges esetek végignézésével azonnal megállapíthatjuk:
02=0,12=1,22=4,32=9,42=16,52=25,62=36,72=49,82=64,92=81.
Többjegyű számok négyzetére pedig azért igaz ez az állítás, mert csak az utolsó jegyüktől függ, hogy mi lesz a négyzetüknek az utolsó jegye.
Általánosabban: két szám szorzatának utolsó jegye csak a számok utolsó jegyétől függ. Ezt könnyen beláthatjuk, ha a szorzás szokásos elvégzési módjára gondolunk, például
27⋅4254¯1081134¯


Az utolsó jeggyel végzett szorzás részletszorzatának utolsó jegyéhez már nem adunk semmit, ez lesz a szorzat utolsó jegye.
Az egyjegyű számok négyzetét megfigyelve még egy megállapítást tehetünk: a páratlan egyjegyű számok négyzetének tizese páros (a fenti felsorolásban: 0, 0, 2, 4, 8). Számpéldák azt mutatják, hogy ez érvényes többjegyű számokra is. Ha ez mindig így van, akkor a csupa 1, 5, 9-ből álló számok sem lehetnek négyzetszámok, hiszen utolsó előtti jegyük páratlan.
Bebizonyítjuk, hogy minden többjegyű páratlan szám négyzetének utolsó előtti jegye páros. Ezt beláthatjuk a négyzetreemelés bármelyik szokásos eljárása alapján, vagy algebrailag a következő módon. Jelöljük a szám utolsó jegyét a-val, az utolsó jegy elhagyásával visszamaradó számot 10 A-val. Ekkor
(10A+a)2≡100A2+20Aa+a2,
és itt az első tag nem befolyásolja a négyzetszám tízesét, a második tag páros jeggyel járul hozzá, és ha a páratlan, akkor a harmadik tag is páros jeggyel járul hozzá, mint arról az esetek végignézésével már az előbb meggyőződtünk.
Most már csak a 4...4 és 6...6 alakú számokról kell bebizonyítanunk, hogy nem lehetnek négyzetszámok. Ezek páros számok, tehát mindegyikük csak páros számnak lehetne a négyzete. A 6...6 szám nem lehet négyzetszám, mert páros szám négyzete 4-gyel is osztható: (2c)2=4c2, viszont 6...6=6⋅1...1 páros, de 4-gyel nem osztható.
Azt is látjuk, hogy páros szám négyzetének a negyedrésze is négyzetszám (c2), viszont 4...4=4⋅1...1, és itt a második tényező egy legalább két 1-esből álló szám, az ilyenekről pedig már beláttuk, hogy nem lehetnek négyzetszámok.
Minden esetet végignéztünk, s így bebizonyítottuk, hogy többjegyű négyzetszám nem állhat egyező jegyekből, mindig van benne legalább két különböző számjegy.
 
II. megoldás. Láttuk, hogy egész számok négyzetének (általánosan: egész számok szorzatának) utolsó jegye csak az alap (a tényezők) utolsó jegyétől függ. Hasonlóan belátható, hogy a szorzat utolsó két jegye is csak a tényezők utolsó két jegyétől függ.
Ezt is bebizonyíthatjuk akár a szorzási eljárás elemzése alapján, akár algebrai jelöléssel. Lássuk az utóbbit. Jelentse a és b a szóban forgó tényezők utolsó két jegyéből álló számot, A és B az elhagyásuk után visszamaradt számot. Akkor maguk a tényezők 100A+a és 100B+b, szorzatuk pedig 10000AB+100Ab+100aB+ab. Az első három tag nem befolyásolja a szorzat utolsó két jegyét, hiszen mindegyiknek a végén legalább két 0 van. Tehát a szorzat utolsó két jegye ‐ mint állítottuk ‐ megegyezik a tényezők utolsó két jegyéből álló számok (a és b) szorzatának utolsó két jegyével.
Ha tehát meg akarjuk állapítani, hogy mi lehet egy négyzetszám utolsó két jegye, elég végignéznünk az egy- és kétjegyű számok négyzetének utolsó két jegyét. Célszerű ehhez elővenni a Négyjegyű Függvénytáblázatot, amelyet a versenyzők ‐ mint általában bármely könyvet ‐ szabadon használhattak. Megállapíthatjuk, hogy egyező jegyekként csak 00 és 44 fordul elő az utolsó két helyen. (Megjegyezzük, hogy a vizsgálandó négyzetszámok legfeljebb négy jegyűek, így a táblázat a kerekítés nélküli, pontos értéküket közli.) Egy csupa 0-ból álló számot nem tekintünk többjegyűnek. Ha volna csupa 4-esből álló többjegyű négyzetszám, akkor volna csupa 1-esből álló is, amint azt az I. megoldásban beláttuk. Ilyen azonban nincs, hiszen az utolsó két jegy nem lehet 11, tehát csupa 4-esből álló négyzetszám sem fordulhat elő. A többjegyű négyzetszámokban tehát csakugyan kell lennie legalább két különböző jegynek.
 

Megjegyzés. A 0,1,...,99 számok négyzete helyett elég csak a 0,1,...,25 számok négyzetét végignézni, mert 25-ön túl új kétjegyű végződés nem lép fel. Egyrészt ugyanis (50-a)2-nek ugyanaz az utolsó két jegye, mint a2-nek, hiszen különbségük, 2500-100a, 100-nak többszöröse, és ha 0≤a≤25, akkor 25≤50-a≤50; másrészt (b+50)2-nek hasonló okból ugyanaz az utolsó két jegye, mint b2-nek, és ha b 0-tól 50-ig változik, akkor 50+b végigfut 50-től 100-ig a számokon.
2. feladat. Rajzoljuk meg azt a négy kört, amelyek érintik egy háromszög oldalegyeneseit, vagyis a beírt kört és a hozzáírt köröket. Bizonyítsuk be, hogy a beírt és bármelyik hozzáírt kör negyedik közös érintője párhuzamos a másik két hozzáírt kör negyedik közös érintőjével.
 

I. megoldás. Az ABC háromszög a oldalegyenese a beírt és az Oa középpontú hozzáírt kör egyik közös belső érintője. Jelöljük e két kör másik közös belső érintőjét a'-vel. Az a egyenes érinti a másik két hozzáírt kört is, mint e körök közös külső érintője. Jelöljük ennek a két körnek a másik közös külső érintőjét a''-vel. Bebizonyítjuk, hogy 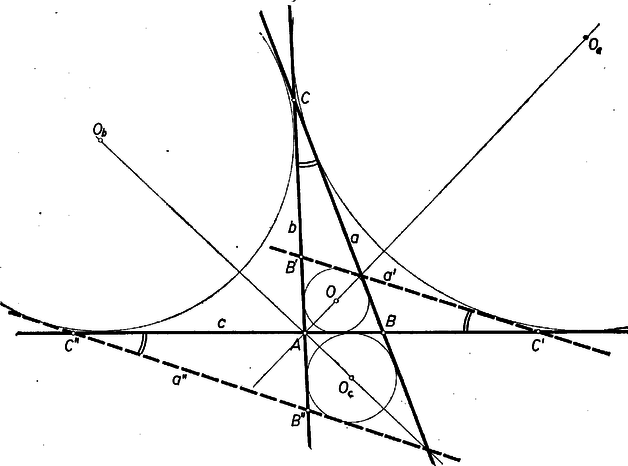a'∥a''.
 




 

Két kör együttesen tükrös a középpontjukon át húzott egyenesre, a két kör úgynevezett centrálisára. Ebből következik, hogy két kör közös belső érintői, és ugyanúgy közös külső érintői is tükrösek a két kör centrálisára. Így pl. a' az a oldal tükörképe az OOa centrálisra vonatkozóan, a-nak az ObOc centrálisra vonatkozó tükörképe pedig a''. Eszerint az a' egyenest két különböző tengelyre vonatkozó egymás utáni tükrözés átviszi az a'' egyenesbe. Tudjuk viszont, hogy két egymást metsző egyenesre való tükrözés együttesen egy olyan elforgatást eredményez, amelynek a szöge a tükörtengelyek egymással alkotott szögének kétszerese, és a forgatás középpontja a két tengely metszéspontja. Az egyik tükörtengely OOa, a b és c egyenesek egyik szögfelezője, a másik ObOc, ugyanennek az egyenespárnak a másik szögfelezője. A két szögfelező, mint tudjuk, merőleges egymásra. Tehát az a' egyenest két egymásra merőleges egyenesre való tükrözés, vagyis az A pont körüli 180∘-os elforgatás viszi át az a'' egyenesbe, és így csakugyan a'∥a''.
Hasonló jelöléssel és gondolatmenettel következik az is, hogy b'∥b'' és c'∥c''.
 
II. megoldás. Az előző megoldás jelöléseit használjuk. Jelöljük továbbá a' és b metszéspontját B'-vel, a' és c metszéspontját C'-vel, a'' és b, ill. a'' és c metszéspontját B''-vel, ill. C''-vel. A szimmetria miatt BC'CB' egyenlő szárú trapéz, tehát húrnégyszög, és így BC'B'∢=BCB'∢. Ugyanezt mondhatjuk a BCC''B'' négyszögről is. Ennélfogva BCB''∢=BC''B''∢. Ezek szerint BC'B'∢=BC''B''∢, és így a'∥a''.
 

3. feladat. Egy köralakú versenypályának egy pontjából egyszerre egy irányban elindult három futó. Az első 6 perc alatt utolérte (lekörözte) a másodikat, 10 perc alatt a harmadikat. Hány perc alatt érte utol a harmadik a másodikat? (A futók sebességét tekintsük egyenletesnek, a pálya szélességét hagyjuk figyelmen kívül).
 
I. megoldás. Legyen a futók sebessége sorban u, v és w, a pálya kerülete k, a keresett idő pedig, ahány perc alatt a harmadik futó lekörözte a másodikat, x. Akkor a megtett utakra a következő egyenleteket írhatjuk fel:
6u=6v+k,vagyis6u-6v-k=0,(1)10u=10w+k,vagyis10u-10w-k=0,(2)xw=xv+k,vagyisxw-xv-k=0.(3)
Az (1) egyenletet 5x-szel, (2)-t 3x-szel, (3)-at 30-cal szorozva u, v és w szorzója mindegyik egyenletben 30x vagy -30x lesz:
30xu-30xv-5xk=0,(4)30xu-30xw-3xk=0,(5)30xw-30xv-30k=0.(6)
(5) és (6) összegéből kivonva (4)-et u, v és w kiesik:
2xk-30k=0.
Minthogy k≠0, ebből x=15. Tehát a harmadik futó 15 perc alatt körözte le a másodikat.
 
II. megoldás. A feladatot sok másféle módon is megoldhatjuk, kevesebb ismeretlennel is, mint az I. megoldásban, sőt egyenlet nélkül is.
Képzeljük, hogy a futók változatlan sebességgel tovább futnak. Az első a másodikat minden 6 perc elteltével, a harmadikat minden 10 perc elteltével lekörözi, tehát fél órával az indulás után az első éppen 5 körrel futott többet, mint a második, és 3 körrel futott többet, mint a harmadik (tehát mindhárman a pálya ugyanazon pontján vannak). Így hát a harmadik futó fél órával az indulás után 5-3=2 körrel futott többet, mint a második. Ebből következik, hogy negyedóránként (15 percenként) körözte le a másodikat.
 
Megjegyzés. Az adatokból az u, v, w és k ismeretlenek nem is számíthatók ki, még az arányuk sem.
 
 Varga Tamás