Cím: Néhány elemi geometriai problémáról
Szerző(k):  Erdős Pál 
Füzet: 1962/május, 193 - 201. oldal  PDF  |  MathML 
Témakör(ök): Szakmai cikkek

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

1. E kis cikkben egy elemi geometriai kérdéssel kapcsolatos megoldott és megoldatlan problémákról lesz szó. Remélem, sikerülni fog az olvasót meggyőznöm, hogy még az elemi geometria évezredek óta vizsgált területén is sok az új és egyszerű segédeszközökkel bizonyítható eredmény.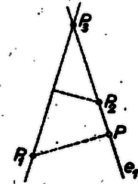
1933-ban olvastam Hilbert‐Cohn-Vossen1 ,,Anschauliche Geometrie'' (szemléletes geometria) című szép könyvét. E könyv geometriai konfigurációkról szóló fejezetének olvasása közben a következő probléma jutott eszembe: Legyen adva a síkban n pont, melyek nincsenek mind egy egyenesen, akkor van oly egyenes, mely ezen n pont közül pontosan kettőn megy át. Úgy gondoltam, ez magától értetődő lesz, de nem tudtam bebizonyítani. Elmondtam e sejtést Gallai Tibornak, aki hamarosan szép bizonyítást talált e tételre. 1936-ban az oslói nemzetközi matematikai kongresszuson Karamata2 kérdezett e tételről, mondotta, hogy egy régi mechanika könyvben olvasta s ő sem tudta bebizonyítani. Elmondtam neki Gallai bizonyítását.
1943-ban kitűztem a problémát az American Mathematical Monthly c. folyóirat probléma-rovatában. Több érdekes megoldás érkezett, a legszebb Kellyé3, mely még Gallaiénál is szellemesebb, s melyet most közlök.

 
 
1. ábra
 

2. Legyenek az adott pontok P1,P2,...,Pn. Kössük össze bármely két Pi-t. Így nyerjük az e1,...,em egyeneseket. Minthogy a pontok nincsenek mind egy egyenesen, m>1. Tekintsük mindegyik Pi távolságát mindegyik ei -től, mely nem megy át Pi-n. Legyen ezen távolságok legkisebbike például P1 távolsága e1-től (a pontok és egyenesek számozása természetesen tetszőleges). Azt állítom, hogy az e1 egyenesen pontosan két Pi van. Jelentse P a P1-ből e1-re bocsátott merőleges talppontját (1. ábra). Ha e1-en három Pi lenne, akkor P valamelyik oldalán legalább két ily pont lenne, e pontok legyenek P2 és P3 úgy, hogy P2 P és P3 között van (esetleg P2 P-vel egybeesik). Ekkor azonban világos, hogy P2 távolsága a P1P3 egyenestől kisebb mint P1P, a P1 pont távolsága az e1 egyenestől (tudniillik P2 távolsága kisebb vagy egyenlő, mint a P1PP3 derékszögű háromszögnek az átfogóra bocsátott magassága, és P1P nagyobb ennél), s ezzel Gallai tételét be is bizonyítottuk.
3. Kelly a probléma eredetét is megtalálta. 1893-ban Sylvester4 közölte e problémát az Educational Times c., azóta megszűnt folyóiratban5. Megoldás e feladatra akkor nem érkezett, s nincs adat arra, vajon Sylvesternek volt-e megoldása problémájára, s így a tételt Gallai tételének nevezik. Kelly bizonyítását Coxeter6 közölte7.
1949-ben megismerkedtem Motzkinnal8. Elmondta, hogy 1933-ban (Sylvesterről s rólunk nem tudva) ő is felvetette e kérdést, s 1939-ben A. Robinson9 bebizonyította a tételt.
4. Gallai tételével kapcsolatban számos további probléma merül fel. Hogy röviden tudjuk kifejezni magunkat, nevezzünk ‐ ha adva van a síkban n pont, melyek nincsenek mind egy egyenesen ‐, közönséges egyenesnek egy olyan egyenest, mely e pontok közül pontosan kettőn megy át. Gallai tétele szerint mindig legalább egy közönséges egyenes van. Ha a pontok általános helyzetben vannak (nincs semelyik 3 egy egyenesen), a közönséges egyenesek száma10 (n2). Ha n-1 pont van egy egyenesen, és az n-edik az egyenesen kívül, akkor a közönséges egyenesek száma n-1. Jelentse mármost f(n) a közönséges egyenesek minimális számát. De Bruijnnel11 sejtettük, hogy f(n) n-nel együtt minden határon túl nő, vagyis akárhogy is adunk meg egy A egész számot, létezik egy csak A-tól függő n0=n0(A) szám úgy, hogy bárhogyan is adunk meg a síkban n0-nál több pontot, amelyek nincsenek mind egy egyenesen, ezek legalább A közönséges egyenest határoznak meg.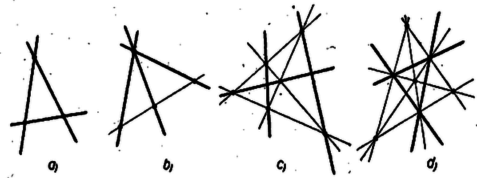
 
 
2. ábra
 

G. Dirac12 bebizonyította, hogy f(n)≧3. E becslés n=3-ra, 4-re, 6-ra és 7-re pontos, amint azt a 2. ábra példái mutatják. Motzkin bebizonyította13, hogy f(n)>n, és ezzel sejtésünket igazolta. Legújabb időben Kelly és Moser14 bebizonyították15, hogy f(n)≧37n; ez megint pontos n=7-re, nincs azonban kizárva, hogy n nagy értékeire a tétel még javítható, például igaz lehetne a következő sejtés: Létezik egy olyan n0 egész szám, hogy ha n>n0 és P1,...,Pn tetszőleges n pont a síkban, melyek nincsenek mind egy egyenesen, akkor ezek legalább n-1 közönséges egyenest határoznak meg. Ez azt jelentené: hogyha n>n0, akkor f(n)=n-1 (ti. már említettük, hogy ha n-1 pont egy egyenesen van, akkor n-1 közönséges egyenest nyerünk, s ezért minden n-re f(n)≦n-1. G. Dirac sejtette, hogy n>7 esetén f(n)≧n2.
5. Még 1933-ban észrevettem, hogy Gallai tételéből következik, hogy ha a síkban n pont van adva, melyek nincsenek mind egy egyenesen, akkor ezek legalább n egyenest határoznak meg, azaz azon egyenesek száma, melyek e pontok közül legalább kettőn átmennek, nem lehet n-nél kisebb. A bizonyítás Gallai tételének segítségével könnyű (lásd az 1183. feladatot).
Nyilvánvaló, hogy e tétel pontos, ha ugyanis n-1 pont van egy egyenesen, s az n-edik pont nincs ezen az egyenesen, akkor e pontok nyilván n egyenest határoznak meg. Sejtettem, hogy ha az n pont olyan, hogy nincs közülük n-1 sem egy egyenesen, és n elég nagy szám, akkor ezek legalább 2n-4 egyenest határoznak meg. Ez kis n-ekre, pl: n=6,7,8-ra nem igaz. A 2. c), d) ábrán és a 3. ábrán n=6,7,8 pont esetén rendre 7, 9, ill. 11 egyenest látunk, 2n-4 pedig ezekre az n-ekre 8, 10, ill. 12. Kelly és Moser a már idézett cikkükben15 a következő általános tételt bizonyítják be: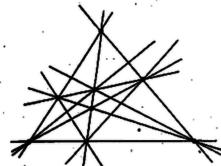
 
 
3. ábra
 

Tegyük fel, hogy az n pont olyan, hogy legfeljebb n-k van közülük egy egyenesen, tegyük fel továbbá, hogy
n≧12[3(3k-2)2+3k-1],(1)
akkor az n pont legalább
kn-12(3k+2)(k-1)(2)
egyenest határoz meg. Nem feltétlenül határoznak meg a pontok (2)-nél több egyenest, mint ezt a szerzők következő példája mutatja: P1,...,Pk legyen k pont a síkban úgy, hogy nincs közülük három egy egyenesen, e a sík egy tetszőleges egyenese, mely a Pi, 1≦i≦k pontok egyikén sem megy át. A (Pi;Pj) 1≦i, j≦k egyenesek ‐ számuk (k2) ‐ az e egyenest a Pk+1,...,Pk+(k2) pontokban metszik. A többi n-k-(k2) pontot az e egyenesen tetszőlegesen vesszük fel. Könnyű belátni, hogy ez az n pont
1+k(n-k)-(k2)=kn-12(3k+2)(k-1)
egyenest határoz meg.
Legyen mármost k=2. ‐ (1) és (2) igazolja sejtésemet, ha n≧27. Kelly és Moser kimutatták, hogy sejtésem n=10-re is igaz (azaz 10 pont, melyek közül nincs 9 egy egyenesen, legalább 16 egyenest határoz meg), s sejtik, hogy a 11≦n≦26 értékekre is igaz. Bebizonyították továbbá, hogy ha n=7,8, 9, akkor legalább 2n-5 egyenest nyerünk, s láttuk (2. c), d) ábra és 3. ábra), hogy 2n-5 nem is javítható.
6. Kelly és Moser eredményei azonban még nem intézik el teljesen az itt felmerülő problémákat. Nyilvánvaló pl., hogy létezik egy oly ck szám, hogy ha adva van n pont, melyek közül legfeljebb n-k van egy egyenesen, akkor e pontok legalább ckkn egyenest határoznak meg, például vehetjük ck-t 1/k-nak. (2)-ből ck-ra ennél lényegesen jobb becslést kaphatunk, de különböző k-ra különbözó ck értékeket. A kérdés azonban az, hogy van-e oly c szám, mely minden k-ra jó. Azaz valószínűleg igaz a következő sejtés: Létezik oly c állandó, (mely nem függ sem k-tól, sem n-től), hogy ha az n pont közül legfeljebb n-k van egy egyenesen, akkor a fellépő egyenesek száma nagyobb, mint ckn (feltehető, hogy a sejtés igaz, ha c=1/10).
Említsük meg még Dirac következő sejtését: Legyen P1,...,Pnn pont a síkban, melyek nincsenek mind egy egyenesen, akkor mindig van egy pont Pi úgy, hogy a (Pi;Pj), 1≦j≦n, i≠j egyenesek közül legalább [n2] különböző van.
Megemlítjük még, hogy Sylvester a következő kérdést vizsgálta: Legyen adva n pont, P1,P2,...,Pn a síkban. Maximálisan hány olyan egyenes lehetséges, mely e pontok közül pontosan hármon megy át? Kimutatta, hogy n=9-re e maximum 10. Könnyű belátni, hogy általában n-re e maximum nem nagyobb, mint 13(n2) (ennyi volna, ha minden PiPj egyenesen 3 pont volna) és Gallai tétele miatt e maximum semmilyen n-re nem érheti el az 13(n2) értéket. Páros n-re e maximum legfeljebb 13(n2)-n6. (Ez abból látható be, hogy minden ponton kell olyan egyenesnek átmennie ez esetben, amin páros számú Pi pont van.) E tételek részletes bizonyítását az olvasóra bízom. Nagyon meglepő azonban, hogy Sylvester kimutatta, hogy e maximum nagyobb, mint 13(n2)-cn, ahol c alkalmas, n-től nem függő állandó. Kérdezhetjük még azt is, hogy mekkora azon egyenesek maximális száma; amelyek az n pont közül pontosan négyen mennek át. Ezt csak n speciális értékeire vizsgálták, és én azt hiszem, hogy nagy n-re e maximum sokkal kisebb nagyságrendű lesz, mint n2, talán kisebb, mint cn, egy alkalmas c állandóval.
7. Most rátérek e kérdések kombinatorikus általánosításaira. Legyenek a1,...,an elemek, A1,...,Am az elemekből alkotott, legalább kételemű csoportok (szokásos szakkifejezéssel halmazok). Feltesszük, hogy minden (ai;aj) pár egy és csakis egy Ai-ben fordul elő. Ha az ai-k pontok, és az Aj-k azon egyenesek, melyek e pontok közül legalább kettőn átmennek, akkor nyilván e feltételt kielégítő rendszert kapunk. Azonban könnyű belátni, hogy lehet olyan ai, 1≦i≦n, Aj, 1≦j≦m rendszert csinálni, mely nem valósítható meg, mint a sík pontjai és egyenesei. Legyen ugyanis n=m=7, és az A-k: (a1,a2,a3), (a1,a5,a6), (a1,a4,a7), (a2,a4,a6), (a2,a5,a7), (a3,a4,a5), (a3,a6,a7). E rendszer nyilván nem valósítható meg a síkban, ti. e rendszernek nincsen közönséges egyenese, azaz nincs oly Aj, mely pontosan két ai-t tartalmaz.
Ennek ellenére fennáll a követező tétel: Ha m>1, akkor m≧n ‐ azaz ha az A-k száma nagyobb, mint egy, akkor legalább n A van. Ez lényeges általánosítása annak a tételnek, hogy n pont a síkban, ha nincs mind egy egyenesen, legalább n egyenest határoz meg.
E tételt Hanani16 bizonyította be először 1938-ban. Én Hanani eredményéről nem tudva, 1941-ben újra felfedeztem e tételt, melyet Szekeres17 is bebizonyított. A legegyszerűbb bizonyítás de Bruijn-től való, melyet most közlök.
8. Két elem ai1 és ai2 nyilván egyértelműen meghatároz egy A halmazt, éspedig azt, amely az (ai1;ai2) párt tartalmazza. Feltevésünk szerint egy és csakis egy ily A van. Hogy röviden tudjam magam kifejezni, az ai elemeket pontoknak fogom nevezni s az Aj halmazokat utaknak.
Jelöljük az ai ponton átmenő utak számát ki-vel, az Aj úton levő pontok számát sj-vel. Nyilván 1<ki<n, és 1<sj<n, minthogy a pontok nincsenek mind egy út mentén, és minden úton legalább két pont van.
A ki-k és sj-k közt könnyen találhatunk egy összefüggést p1. a következő szemléletes meggondolással: képzeljük az utakat villamosvonalaknak, amelyeknek minden pontban (kereszteződésnél) megállójuk van 18. Egy alkalommal minden vonalon végighaladt egy villamos, és mindegyikre minden megállónál egy utas szállt fel. Ekkor az ai kereszteződésnél ki felszálló volt, az Aj vonalon sj utas utazott, tehát az összes utasokat egyrészt útvonalak, másrészt állomások szerint összeszámolva a következő azonosságot kapjuk:
s1+s2+...+sn=k1+k2+...+kn.(3)

Feltehetjük, hogy a pontok a rajtuk átmenő utak csökkenő száma szerint vannak rendezve, tehát
kn≦ki,  ha  i=1,2,...,n,(4)
továbbá, hogy az an-en az A1,A2,...,Akn utak mennek át. Jelöljük kn-et, miután sok szó lesz még róla, rövidebben v-vel.
Keressünk összefüggéseket a k-k és s-ek közt. Ha az Aj út nem megy át az ai ponton, akkor ai-t Aj minden egyes pontjával más-más út köti össze, mert különben volna két olyan út, amelyek két különböző pontban találkoznak, pedig feltettük, hogy ilyen nincs. Így, ha Aj nem megy át ai-n, akkor
ki≧sj.(5)

Ezt alkalmazhatjuk kn és sv+1,sv+2,...,sm-re:
kn≧sj(j=v+1,v+2,...,m).

Ezeket összeadva
(m-v)kn≧sv+1+sv+2+...+sm.(6)

Az s1,s2,...,sv-t is tudjuk becsülni k-kkal (5) alapján, ugyanis A1 átmegy egy an-től különböző ponton ‐ feltehetjük, hogy ezt jelöltük a1-gyel ‐, mert minden út legalább két ponton halad át. Ekkor A2,...,Av nem mehet át a1-en, mert két út legfeljebb egy pontban találkozik, így (5) szerint fennáll pl.
k1≧s2.

De A2 is átmegy egy an-től (és a1-től) különböző ponton, mondjuk a2-n. Ezen A3,...,Av nem megy át, tehát pl.
k2≧s3.

Hasonlóan haladva tovább, végül az Av-1-en találunk egy an-től különböző av-1 pontot, amelyen Av nem megy át, Av-n pedig egy av pontot, amin az előző Ai-k, p1. A1 nem megy át. Így (5) alapján a következő egyenlőtlenségeket kapjuk:
k1≧s2,k2≧s3,...,kv-1≧sv,kv≧s1.

Ezeket összeadva és hozzájuk adva (6)-ot, azt kapjuk, hogy
k1+k2+...+kv+(m-v)kn≧s1+s2+...+sm.

Írjuk itt be a jobb oldal helyébe (3) jobb oldalát, majd alkalmazzuk kv+1,kv+2,...,kn-re (4)-et, kapjuk, hogy
k1+k2+...+kv+(m-v)kn≧k1+k2+...+kn≧≧k1+k2+...+kv+(n-v)kn.


Innen
(m-v)kn≧(n-v)kn,
és mivel kn>1,
m≧n.
Ezzel bebizonyítottuk Hanani tételét.
9. Az egyenesekre tárgyalt problémához hasonlóak körökkel kapcsolatban is felmerülnek. Érvényes Gallai tételének következő általánosítása: Legyenek adva a síkban a P1,P2,...,Pn pontok (n>3), amelyek nincsenek mind egy körön, akkor van olyan kör, amelyik pontosan három Pi-n megy át. A tétel (mely említve van a 13 lábjegyzetben idézett cikkben), Gallai tételéből könnyen következik az inverzió, más néven körre vonatkozó tükrözés nevű transzformáció segítségével.19 Tegyük fel ugyanis, hogy a tétel nem volna igaz. Ekkor volna egy olyan pontrendszer, amelynek bármely három pontján átmenő kör egy negyedik Pi-n is átmenne, így többek közt minden (P1,Pi,Pj) ponthármason átmenő kör átmenne egy negyedik Pk ponton is. Alkalmazzunk ekkor inverziót egy P1 középpontú körre, a Pi pont képét jelöljük Qi-vel (i=2,3,...,n). Ebben a pontrendszerben a QiQj egyenes a P1, Pi, Pj pontokon átmenő kör képe, s így feltétel szerint átmegy legalább még egy Qk ponton. Ez azonban Gallai tétele szerint csak úgy lehet, ha Q2,Q3,...,Qn mind egy egyenesen van, de ez az egyenes akkor egy P1-en is átmenő kör képe volna, holott feltétel szerint nincs az összes Pi egy körön. Lehetetlenségre jutottunk, kell tehát, hogy a körökre vonatkozó tétel is igaz legyen.
Nem látszik azonban könnyűnek a következő kérdés, melyet évekkel ezelőtt felvetettem: Legyen adva n pont a síkban, melyek nincsenek mind egy körön. Tekintsük az összes köröket, melyek a pontok közül hármon átmennek. Igaz-e, hogy így legalább 1+(n-12) kört kapunk? Ha n-1 pont egy körön van, akkor pontosan 1+(n-12) kört kapunk.
A megfelelő kombinatorikus általánosítás így hangzik: Legyen a1,a2,...,an n elem, A1,...,Am, m>1 az a-kból alkotott legalább három elemű halmazok úgy, hogy mindegyik az ai-kből álló hármas egy és csakis egy A-ban fordul elő. Mekkora m minimális értéke? ‐ A párok esetén a geometriai és a kombinatorikus probléma megoldása, amint láttuk, ugyanaz volt, minimális értéke mindkét esetben n. Valószínű azonban, hogy ternók (három elemű halmazok) esetén m minimuma a kombinatorikus esetben kisebb, mint a geometriai problémánál. Hanani bebizonyította a következőt: Adjunk meg tetszőlegesen egy kis ε pozitív számot; ehhez mindig található egy n0 úgy, hogy ha n>n0, és adva van n elem, a1,a2,...,an, akkor m értéke a kombinatorikus problémánál kielégíti a következő egyenlőtlenséget:
m>(1-ε)n384.(7)

Hanani bizonyítása, mely eddig még nem jelent meg nyomtatásban, a következő: Legyen az Ai halmaz elemeinek a száma si. Feltehetjük, hogy a halmazokat pl. a bennük levő elemek száma szerint csökkenő sorrendbe rendeztük, tehát
s1≧s2≧...≧sm.
Az összes hármasok száma, amiket az n elemből képezhetünk,
(n3)=n(n-1)(n-2)6.
Ezek mindegyike előfordul egy halmazban és csak egyben, viszont az i-edik halmazban
(si3)=si(si-1)(si-2)6
hármas fordul elő, így
(n3)=(s13)+(s23)+...+(sm3)≦m(s13),
amiből
m≧(n3)(s13)=n(n-1)(n-2)s1(s1-1)(s1-2)>n3s13,
minthogy s1<n miatt ns1<n-1s1-1<n-2s1-2. Ebből következik (7) abban az esetben, ha
s1≦24n=2n24.

Arra az esetre, ha s1 ennél nagyobb érték, gondoljuk meg mindenek előtt, hogy A1 elemei közül egyrészt a többi Ai mindegyike legfeljebb 2-t tartalmazhat, mert minden hármas csak egy Ai-ben fordul elő, másrészt minden A1-ben szereplő elempár legalább még egy Ai-ben előfordul, mert különben a kérdéses elempárból és egy A1-ben nem szereplő elemből álló hármasok egy halmazban sem szerepelnének. Mivel A1 elemeiből (s12) pár képezhető, így A1-en kívül legalább még ennyi halmazunk van:
m≧1+(s12)>s1(s1-1)2=s122(1-1s1).
Ez abban az esetben adja (7)-et, ha s1 elég nagy, és n elég nagy; pl. ha s1≧2n34, akkor
m>2n34(2n34-1)2=n32(1-12n34);
s így teljesül (7), ha n elég nagy (pl. ha 12n34<ε, tehát n>12ε43..
Ha végül
2n24<s1<2n34,(8)
akkor vizsgáljuk meg azt is, hány halmazban kell egy A1-beli elempárnak előfordulnia ahhoz, hogy minden hármas szerepelhessen, amely ebből a párból és még egy, A1-ben nem szereplő elemből áll.
Egy-egy A1-beli párból n-s1 számú ilyen hármas alkotható, mert ennyi elem nem szerepel A1-ben. Másrészt egy Ai-nek, amely két A1-beli elemet tartalmaz, emellett legfeljebb s1-2 további eleme lehet, mert nem lehet s1-nél több eleme. Így ahhoz, hogy egy A1-beli párt tartalmazó összes hármas előfordulhasson, ennek a párnak A1-en kívül még legalább n-s1s1-2 halmazban kell előfordulnia. Mivel A1 elemeiből (s12) pár alkotható, így
m≧1+(s12)n-s1s1-2>s1(s1-1)(n-s1)2(s1-2)>s1(n-s1)2==n24-(n2-s1)22.


A (8) feltételnek eleget tevő s1 értékek kisebbek n/2-nél, ha n≧32, az ilyen n-ekre tehát csökkentjük a nyert kifejezés értékét, ha s1-et nála kisebb számmal helyettesítjük. Eszerint a (8) alatti s1 értékekre (a nyert korlát jobban kezelhető utolsó előtti alakját használva)
m>2n24(n-2n24)2=n384-n2=n384(1-24n).

Ezek szerint a (8) feltételnek eleget tevő s1 értékekre is teljesül (7), amint n elég nagy (  egyrészt  n≧32,  másrészt  24n<ε,  azaz  n>2ε2). Az n-re adódott korlátok közül a legnagyobbat választva n0-nak, bármekkora is s1, mindig teljesül (7), amint n>n0. Ezzel Hanani tételét bebizonyítottuk.
Hanani azt is bebizonyította, hogy ha n=u2+1, ahol u prímszámhatvány, akkor
m≦u(u2+1)[=nn-1].(9)

Hanani sejti, hogy itt m=u(u2+1). (7) és (9)-ből az analitikus számelmélet eszközeivel könnyen belátható, hogy a kombinatorikus problémánál m minimumának nagyságrendje n3/2, pontosabban minden pozitív ε-hoz van oly n0, hogy ha n>n0, akkor
(1-ε)2-3/4n3/2<m<(1+ε)n3/2.(10)

(10) bal oldalát már bebizonyítottuk, a jobb oldallal itt nem foglalkozhatunk. E problémákat hármasokról l-esekre is általánosíthatjuk minden l>3 esetén, de ezzel most nem foglalkozunk.
 
 Erdős Pál
1David Hilbert (1862‐1943) a jelenkor egyik legkiválóbb matematikusa, főleg Göttingában működött. S. Cohn-Vossen német geométer, a hitlerizmus miatt emigrált s Leningrádban lett professzor, hol még a harmincas években elhunyt.

2J. Karamata jugoszláv matematikus, jelenleg a genfi egyetemen professzor. Főleg végtelen sorokra vonatkozó vizsgálatai tették ismertté.

3L. M. Kelly a Missouri-i egyetemen müködött, jelenleg East Lansingban, Michigan állam egyetemén professzor.

4J. J. Sylvester (1814‐1897) kiváló angol matematikus, főleg számelmélettel s geometriával foglalkozott, az angliai oxfordi egyetemen, majd a John's Hopkins University-n (Baltimore, USA) működött. Ő alapította az első amerikai matematikai folyóiratot, a most is megjelenő American Journal of Mathematics-et.

511851. kérdés, 59. kötet 90. old.

6H. S. M. Coxeter kiváló kanadai geométer, a torontói egyetem professzora.

7American Mathematical Monthly 55 (1948) 26-28. oldal.

8T. S. Motzkin az USA-ban élő izraeli matematikus. Jelenleg Los Angelesben a californiai egyetemen professzor.

9A. Robinson jelenleg a jeruzsálemi héber egyetemen professzor.

10(n2)-vel (olv. n a 2 fölött) jelölik az n(n-1)/2 számot. Ennyi pár alkotható n elemből; ugyanis mindegyik elem a többi n-1-gyel állítható párba, de az így megszámlált n(n-1) pár közt mindegyiket kétszer vettük számításba (mindegyik eleménél). A későbbiekben szükségünk lesz az n elemből kiválasztható hármasok számára is. Minden elem a tőle különböző n-1 elemből alkotható (n-12) párral összekapcsolva alkothat egy-egy hármast. Ilyen módon n(n-12) hármast számoltunk meg, de minden hármast 3-szor vettünk tekintetbe, tehát a kiválasztható hármasok száma n3(n-12)=n(n-1)(n-2)6. Ezt így szokás jelölni: (n3) (olv. n a 3 fölött).

11N. G. de Bruijn holland matematikus, munkatársam, kivel több közös cikkem van.

12G. Dirac magyar származású angol matematikus, a világhírű angol fizikus, P. Dirac fogadott fia.

13Th. Motzkin, The lines and planes connecting the points of a finite set. Transactions of the American Mathematical Society 70 (1951) 451‐464. Motzkin Gallai tételének érdekes többdimenziós általánosításait is tárgyalja.

14W. O. J. Moser kanadai matematikus, a manitobai egyetemen, Winnipegben professzor.

15L. M. Kelly and W. O. J. Moser, On the number of ordinary lines determined by n points, Canadian journal of Mathematics, 10 (1958) 210-219.

15

16H. Hanani izraeli matematikus, kollégám a haifai műegyetemen.

17Szekeres György Ausztráliában működő magyar matematikus.

18Az ai-k és Aj-k mindig szemléltethetők ilyen (általában nem egyenes) villamosvonalakkal. Ezeknek esetleg a kijelölt pontokon kívül is lesz kereszteződésük, de mi csak a kijelöltekkel foglalkozunk.

13

19Ez a sík egy olyan átalakítása, amelynél egy adott kör pontjai helyben maradnak, a kör középpontjának nincs megfelelője, és minden ezen a középponton átmenő kör egy egyenesbe megy át.