Kezdőlap


Cím:	Pontrendszer szabad mozgása nehézségi erőtérben
Szerző(k):	Holics László
Füzet:	1961/december, 225 - 231. oldal	PDF \| MathML
Témakör(ök):	Szakmai cikkek

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Lapunk 154. feladatának megoldásai indokolttá teszik, hogy a mechanika egyik alapvetően fontos problémájával, a gravitációs erőtérben való szabad mozgással foglalkozzunk. Az alábbiakban feltételezzük, hogy az olvasó előtt a gravitációval és a körmozgással kapcsolatos középiskolai anyagrészek ismeretesek. Vizsgálni fogjuk speciális esetben a gravitációs erőtérben mozgó, két testből álló szabad pontrendszer viselkedését, ha a rendszer tagjai között belső erők hatnak. A feladat problémafelvetésének megfelelően legyen az erőtér forrása kizárólag a Nap, és a pontrendszer álljon a Föld és a hajó pontoknak tekinthető testjeiből. Vizsgálatunk tárgya: a hajó súlyának megváltozása speciális esetekben. A 154. feladat első részének kérdései: Mikor könnyebb a hajó, délben vagy éjfélkor? Hány ponddal könnyebb a hajó, ha a tömege $m_{h} = 15 \cdot 10^{3}$ tonna? Vizsgáljuk meg a hajó súlyát délután 6 órakor is!

Első pillanatra látszik, hogy itt az ár‐apály jelenséggel kapcsolatos problémával állunk szemben. Aki ismeri az ár‐apály jelenséget, tudja, hogy a ,,dagály'' nemcsak a Föld egyik felén következik be, hanem azzal egyidőben a Föld átellenes részén is. A mi feladatunk helyes megoldásának kulcsa azonos a most említett ár‐apály jelenség megoldásának magyarázatával is. Nézzük meg közelebbről.

A 154. feladat első kérdésére a válasz első közelítésben (kis elhanyagolásokkal) igen egyszerű, de ugyanakkor igen váratlan: a hajó súlya éppen akkora délben, mint éjfélkor, vagyis súlyváltozás nincs! Hogy ezt belássuk, menjünk végig az alábbi gondolatmeneten. Határozzuk meg először is, hogy mit értünk a hajó súlyán. Több beérkezett dolgozattal ellentétben nem a hajóra ható összes gravitációs erők eredője a hajó súlya, hanem az az erő, amellyel a hajó a Földet (vizet) nyomja. A későbbiek során belátjuk, hogy ez a két dolog nem ugyanaz. A hajó így definiált súlyát mérhetjük pl. egy olyan rugós erőmérővel, melynek egyik vége a Földhöz van mereven rögzítve, a másik végére helyezzük a hajót.
A déli és éjféli súlyok közötti különbség meghatározására hibás az a következtetés, amely szerint, mivel délben a Nap felfelé vonzza a hajót, éjfélkor pedig lefelé, egyszer levonódik, másszor hozzáadódik ez a vonzás a hajónak a Föld okozta súlyához, vagyis délben könnyebb, éjfélkor nehezebb lesz a hajó. (Akkor lenne így, ha a Föld az égen rögzítve lenne.) Ez a következtetés figyelmen kívül hagyja azt a tényt, hogy a Nap a Földet is épp úgy vonzza, mint a hajót, aminek következtében a Nap gravitációs erőterében mindketten egyformán gyorsulnak a Nap felé, s így a Nap vonzó hatása nem járul hozzá a hajó súlyának kialakításához! Szemléletesen: amennyire gyorsítja maga felé a Nap délben a hajót, ugyanannyira gyorsítja a Földet is. Éjfélkor ugyanez érvényes fordított irányokkal: amennyivel növeli a Nap a hajóra ható földi

g

-t, ugyanannyival hat magára a Földre is; mintegy ,,kigyorsítja'' a Földet a hajó alól. Súlycsökkenés tehát nincs: szabadon mozgó (az erőtér hatására minden részében egyforma gyorsulást szenvedő) rendszer tagjai között fellépő ún. belső erőket nem befolyásolja a rendszer minden tagjára egyformán ható külső erőtér!
Nehézséget okozhat a kezdő számára, hogy a Föld pályamozgása során nem közeledik valóban a Naphoz, s így nem látszik elég szemléletesen a Nap felé irányuló gyorsulás, amelyben a Föld és a hajó egyformán részt vesz, s amire gondolatmenetünket alapoztuk. Valóban, a feladatnak ez az egyik legszebb, fizikus szemléletet követelő pontja: felismerni, hogy a gyorsulás független a mozgás irányától, és hogy a ,,pályagörbítő'' (mozgás irányára merőleges, tehát sebességet nem növelő) gyorsulás egyenértékű a szabadesés gyorsulásával!

Képzeljük el könnyebbség kedvéért a következőket: a hatodik emeleten drótkötélhez rögzített liftszekrényben áll egy asztal, és ezen az asztalon két test van elhelyezve egymás felett, s ezeket valamilyen erő, pl. rugó szorítja össze. Ekkor az asztalon fekvő testet a rajta levő test saját súlyánál fogva valóban nagyobb erővel nyomja mint a közöttük ható egyéb vonzó erő. Ez a helyzet a szilárdan rögzített asztalon. Vágjuk most el a liftet tartó drótkötelet. Ekkor a lift szabadon kezd zuhanni a jól ismert

g

nehézségi gyorsulással. Nyilvánvaló, hogy ekkor már nem nyomja a liftben azzal együtt szabadon eső felső test az alatta levőt, csak a köztük ható rugó erejével, mert most a lift is, az asztal is, az alsó és felső test is egymás mellett szabadon esnek, egyformán gyorsulnak a Föld hatására. Nem változtat ezen a tényen az sem, ha liftünknek valami módon egy vízszintes irányú kezdősebességet adunk. Ekkor a mozgás két részből tevődik össze, egy vízszintes irányú egyenletes mozgásból és egy szabadesésből, aminek eredménye mindössze az, hogy a pálya parabola lesz, ami a szabadesés gyorsulását, tehát a rendszer belső erői viszonyának alakulását nem befolyásolja. Ha pedig igen nagyra választjuk ezt a vízszintes kezdősebességet, elérünk egy olyan határhoz, amelynél a nagy távolságok berepülése miatt már a Föld centrális erőterével kell számolnunk (nem tekinthetjük többé homogénnek), s az elhajított rendszer az ellipszis pályák egyikét írja le. Végül ‐ s most érkeztünk feladatunk esetéhez ‐ ha a ,,vízszintes'' sebesség elér egy kritikus értéket, az ún. ,,körsebesség'' (Föld körül elhajított test esetén az ,,első kozmikus sebesség'') értékét,a rendszer a szabadesés gyorsulásának megléte mellett már állandó körpályán fog keringeni. Szemléletesen: hiába görbül a pálya, nem éri el többé a körülkeringett égitestet. Ekkor a szabadesés gyorsulása mint a körmozgás centripetális gyorsulása lép fel, amely ‐ mint láttuk ‐ lényegileg ugyanolyan szerepet játszik, mint a szabadon eső lift esetében a benne levő testek kölcsönhatására vonatkozóan: azaz nem befolyásolja azokat! A Nap vonzó ereje azonos centripetális gyorsulásra kényszeríti Földünket a rajta levő hajóval együtt. A feladat első kérdésére adandó válasz tehát első megközelítésben az, hogy a hajó súlya egyenlő minden napszakban.
Vizsgáljuk meg most, hogy mennyire pontos ez a megállapítás, mennyire teljesülnek azok a feltételek, amelyeket kihasználtunk gondolatmenetünk alatt?

Lényeges része volt kiindulásunknak az, hogy a rendszer minden tagjára egyformán ható erőtérrel számoltunk. Mennyire valósul meg feladatunk esetében ez a feltevés? Ez akkor igaz, ha az erőtérnek az a része, ahol a vizsgált testek vannak, homogén. Így van-e ez a feladatunkban? Igen nagy pontossággal így. A Nap

150 \cdot 10^{6}

km távolsága a földsugár 6370 km-es hosszához képest igen nagy, így az erővonalak majdnem párhuzamosak, a tér homogénnek tekinthető. (Gondoljunk a Napból érkező fénysugarak ,,párhuzamosságára''.

tg α < 8, 6 \cdot 10^{- 5}

! Rajztáblán vonalzóval gondosan kihúzott párhuzamos vonalak általában jobban eltérnek a párhuzamostól, mint a Nap erőterének a Föld tartományán keresztül haladó erővonalai!) A kérdés gyakorlati részét tehát elintéztük. Ám ár‐apály jelenség mégis van; kérdés, mi okozza ilyen körülmények mellett ezt a jelenséget? Finomítsuk vizsgálatunkat, és nézzük meg az elhanyagolásmentes helyzetet, midőn az erőtér kicsiny inhomogenitását is figyelembe vesszük.

Az ember az előzőek után már gyanakvó, és könnyen azt hinné, hogy inhomogén térben sem lesz különbség a két helyzetbeli súly között, mert igaz, hogy délben más, mégpedig nagyobb vonzóerővel hat a Nap a hozzá közelebb eső hajóra, mint a Földre, éjfélkor viszont a Földre hat nagyobb vonzó erővel, mint a távolabbi hajóra, csakhogy közben fordult egyet a Föld, s így a déli és éjféli helyzetek között súlykülönbség megint nem lesz, mert mindkét hatás egyformán ,,könnyítő''. Szemléletesen: amennyivel nagyobb átlagos térerősségű térrészben van a hajó délben, mint a Föld, annyival nagyobb erősségű térben lesz a Föld éjfélkor, mint a hajó, s így a hajó és a Föld gyorsulásának különbsége végül is kiegyenlítődik.(Egyszer a hajót gyorsítja el a Nap a Földtől, másszor pedig a Földet a hajótól, ami lényegében ugyanaz.) A kétkedés jogos,mert a helyzet valóban ez, de ismét csak első megközelítésben. Ha tovább fokozzuk megfigyelésünk pontosságát, észre kell vennünk, hogy ‐ bár igen kis mértékben ‐ a hajó tömegközéppontja és a Föld tömegközéppontja helyén uralkodó térerősségek különbsége más délben, mint éjfélkor, mert míg a Föld fél nap alatt közelítőleg állandó távolságban tartózkodik a Naptól, a hajó egy földátmérővel távolabb került a Naptól éjszakára. Mivel pedig a térerősség

1 / R^{2}

függvényében csökken, így a nem lineáris változás miatt a déli térerősségkülönbség és az éjféli térerősségkülönbség között különbség lesz, nem rontják le pontosan egymást! (A Földre és hajóra ható, Napból származó gravitációs erők különbsége egy kicsit más lesz délben, mint éjfélkor.) Így az inhomogenitás nemlineáris volta okoz csak súlykülönbözetet!

Több megoldó

R

mellett elhanyagolta

r

-et, a földsugarat. Fizikailag eleve rossz eredményt kapott, mert ezzel elvileg egy pontba egyesítette a hajót és a Földet, így elvileg azonossá vált a Nap terében a gyorsulásuk, vagyis effektus nem lehet. (Legfeljebb

r / R

magasabb hatványai hanyagolhatók el bizonyos kifejezésekben.)
Vizsgáljuk meg most ezek alapján a hajó súlyának változását a déli, du. 6 órai és éjféli helyzetek között. Az alábbi gondolatmenetből azonnal kitűnik, hogy a hajó legkönnyebb délben, legnehezebb du. 6 órakor, ennél könnyebb, de a déli helyzetnél nehezebb éjfélkor. Tehát a déli és éjféli helyzetek között súlynövekedés mutatkozik az éjféli helyzet javára. Legnagyobb a súlynövekedés a déli ‐ délután 6 órai átmenet alkalmával. Ennek az az oka, hogy a két helyzet közül csak az egyik esetben van a két testre ható gravitációs erőben inhomogenitásból eredő különbség: délben, amikor a hajó közelebb van a Naphoz, mint a Föld. Délután 6 órakor igen kis hibával egyenlő távolságra vannak a Nap középpontjától, így a Nap okozta gyorsulás pontosan egyenlő a pontrendszer mindkét tagjára. A rugós erőmérő ekkor azt az erőt méri, amely a Föld és a hajó között lép fel erőmentes térben (mintha a Nap nem is léteznék). Nevezzük ezt az erőt a hajó ,,abszolút súlyának''. A továbbiakban ehhez viszonyítjuk a súlyokat. (A továbbiakban egyszerűen ,,súly''-nak nevezzük a külső tér által befolyásolt súlyt). Az éjféli helyzetben ismét könnyebb a hajó, mint 6 órakor volt, mert a közelebb levő Földet nagyobb gyorsulásra kényszeríti a Nap, így a hajó ,,lemaradni igyekszik''. Ez a másodszori súlycsökkenés azonban nem egyezik meg az első súlynövekedéssel, mert az inhomogenitásból eredő különbség más, mégpedig kisebb, mint a dél ‐ du. 6 órai átmenetben. (Egyre távolodva a Naptól, a tér adott felületen keresztül haladó erővonalai egyre ,,párhuzamosabbak'', a tér egyre homogénebb! Ezért kisebb a második átmenetnél a súlykülönbség, mint az elsőnél.) Így az ellentétes változások (súlynövekedés, majd súlycsökkenés) nem rontják le pontosan egymást. Feladatunk lesz a maradék súlyváltozás kiszámítása.

Eddig csak a Nap hatásáról volt szó. A Hold ár‐apály hatásának a mértéke nagyobb, bár tömege 27 milliószor kisebb a Nap tömegénél. A nagyobb hatás oka az, hogy a Hold jóval közelebb van a Földhöz, mint a Nap (a Nap 390-szer messzebb van!). És ebben a közelségben nem a gravitációs erő abszolút nagysága a lényeg (a Nap gravitációs gyorsulása nagyobb a Föld helyén, mint a Hold okozta gravitációs gyorsulás!), hanem a Hold terének inhomogenitása sokkal nagyobb, mint a Nap terének inhomogenitása (a Föld körül).

Az erőhatások függetlensége elve alapján a Nap és a Hold hatásai vektoriálisan összegeződnek, feladatunk esetében egyszerűen algebrailag. Mielőtt a számításokat elvégezzük, összefoglalásul tekintsük át eddigi megállapításainkat:
A feladat első részére adandó válasz: mivel a Nap igen távol van, a Föld környezetében tere homogénnek tekinthető. Ebben az esetben (első közelítésben) semmiféle súlycsökkenés nincs. Pontosabb számításoknál figyelembe vesszük a Nap terének inhomogenitását: az erővonalak széttartóak, a hajó jobban gyorsul a Nap felé, mint a Föld, így a 6 órai helyzethez képest van némi súlycsökkenés. Éjfélkor viszont a Föld gyorsul jobban a Nap felé, így ismét súlycsökkenés áll elő a 6 órai helyzethez képest. Ha a Nap terének erőssége lineárisan csökkenne, ez a hatás éppen kiegyenlítené egymást; vagyis az éjféli és déli helyzetekben egyenlő lenne a hajó súlya, tehát inhomogén esetben sem volna súlykülönbözet. Mivel azonban a gravitációs tér változása a távolsággal nem lineáris, így a csökkenések különbsége ad egy megmaradó súlykülönbözetet.
Az ár‐apály jelenség magyarázata: a Holdhoz közelebb levő és az azzal átellenben levő tengervíz könnyebb lesz (fajsúlya csökken), míg az ezek között helyet foglaló víztömegek fajsúlya maximális, aminek következtében hidrosztatikai nyomáskülönbség keletkezik, amely két átellenes irányba történő víztömeg áramlással egyenlítődik ki. (l. a 2. ábrát.)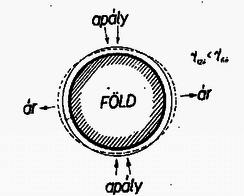

2. ábra

Ezek után megoldhatjuk feladatunkat, amelynek szövege a következő:

154. Mikor könnyebb a hajó, délben, vagy éjfélkor? (A hajó az Egyenlítőn tartózkodik, Nap‐Föld távolság

R = 150 millió km

, Naptömeg

M = 2 \cdot 10^{33} g

, Földtömeg

m = 6 \cdot 10^{27} g

, Földsugár

r = 6370 km

, a gravitációs állandó

= 6, 67 \cdot 10^{- 8} CGS

.) Hány ponddal könnyebb a hajó, ha tömege

m_{h} = 15 \cdot 10^{3} tonna

? Más égitestek hatását ne vegyük figyelembe. Vizsgáljuk meg a hajó súlyát délután 6 órakor is! Számítsuk ki a különbözetet teljes napfogyatkozáskor a Föld két átellenes pontján, valamint ott, ahol 6 óra van. (Holdtömeg

M_{H} = 7, 4 \cdot 10^{25} g

, Föld‐Hold távolság

r_{H} = 384400 km

I. megoldás: Válasszuk vonatkoztatási rendszerünknek az inerciarendszerek egyikét. Legyen a hajó (du. 6 órakor mérhető) ,,abszolút súlya'' ,,erőmentes térben'' vagyis csak a Föld hatására

G_{0}

. Számítsuk ki a hajó megváltozott súlyát az 1-es helyzetben (l. az 1. ábrát).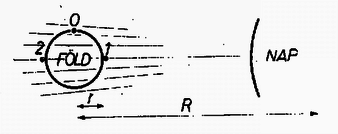

1. ábra

Itt valamivel könnyebb a hajó, mert a hozzá közelebb eső Nap jobban vonzza, mint a távolabbi Földet. A súlykülönbözetet megkapnánk, ha a hajó tömegét szoroznánk a Nap terének a hajó helyén okozott gravitációs gyorsulásával, ha a Föld szilárdan rögzítve lenne. Mivel azonban a Föld is esik a Nap vonzó hatására, csak a Föld és a hajó gyorsulásainak különbsége marad súlycsökkentő hatással.
A hajó gyorsulása:

g_{h_{1}} = γ \frac{M}{{(R - r)}^{2}}

,
a Föld gyorsulása:

g_{f} = γ \frac{M}{R^{2}}

.
A gyorsulások különbsége:

g_{h_{1}} - g_{f} = γ M (\frac{1}{{(R - r)}^{2}} - \frac{1}{R^{2}}) > 0

Így a 0 és 1-es helyzetek között a súlykülönbség (6 óra és dél között):

\begin{matrix} Δ G_{0,1} = m_{h} (g_{h_{1}} - g_{f}) = m_{h} M γ [{(R - r)}^{- 2} - R^{- 2}] . \end{matrix}

Tehát a teljes súly délben:

\begin{matrix} G_{1} = G_{0} - Δ G_{0,1} = G_{0} - m_{h} γ M [{(R - r)}^{- 2} - R^{- 2}] . \end{matrix}

Számítsuk ki a 6 órai és éjféli helyzetek között a súlykülönbséget! (

g_{f}

eközben változatlan marad.)
A gyorsuláskülönbség:

\begin{matrix} g_{f} - g_{h_{2}} = γ M (\frac{1}{R^{2}} - \frac{1}{{(R + r)}^{2}}) > 0. \end{matrix}

Így a 0 és 2-es helyzetek között a súlykülönbség:

\begin{matrix} Δ G_{0,2} = m_{h} (g_{f} - g_{h_{2}}) = m_{h} γ M [R^{- 2} - {(R + r)}^{- 2}] . \end{matrix}

Tehát a teljes súly éjfélkor:

\begin{matrix} G_{2} = G_{0} - Δ G_{0,2} = G_{0} - m_{h} γ M [R^{- 2} - {(R + r)}^{- 2}] . \end{matrix}

Látjuk, hogy mindkét szélső helyzetben kisebb a hajó súlya a 6 órai súlynál. Ez a különbség igen kicsiny. Még kisebb tehát a különbségek különbsége: a déli és éjféli helyzetek között mérhető súlycsökkenés. Ezt megkaphatjuk, ha a két 6 órára vonatkoztatott súlycsökkenést kivonjuk egymásból, ugyanis:

\begin{matrix} Δ G_{1,2} \equiv G_{2} - G_{1} = G_{0} - Δ G_{0,2} - (G_{0} - Δ G_{0,1}) = Δ G_{0,1} - Δ G_{0,2} > 0. \end{matrix}

(

Δ G_{0,2}

azért kisebb, mint

Δ G_{0,1}

, mert a Föld‐hajó rendszer ekkor van átlagban messzebb a Naptól, vagyis az inhomogenitás ekkor kisebb! Íme most láthatjuk, hogy a különbségek különbsége miért és hogyan adódik.)
Az eredő súlycsökkenés a feladatban kérdezett déli és éjféli helyzetek között:

\begin{matrix} Δ G_{1,2} = γ m_{h} M (\frac{1}{{(R - r)}^{2}} - \frac{2}{R^{2}} + \frac{1}{{(R + r)}^{2}}) = γ m_{h} M \frac{6 R^{2} r^{2} - 2 r^{4}}{{(R^{2} - r^{2})}^{2} R^{2}} . \end{matrix}

Ezzel megadtuk a feladat első kérdésére a választ általánosan. Ha egyszerűen megfelelő átírást alkalmazunk, megkapjuk külön a Hold által okozott súlycsökkenést:

\begin{matrix} Δ G'_{1,2} = γ m_{h} M_{h} (\frac{1}{{(R_{H} + r)}^{2}} - \frac{2}{R_{H}^{2}} + \frac{1}{{(R_{H} - r)}^{2}}) = γ m_{h} M_{h} \frac{6 R_{H}^{2} r^{2} - 2 r^{4}}{{(R_{H}^{2} - r^{2})}^{2} R_{H}^{2}} . \end{matrix}

Látható, hogy

Δ G'_{1,2} > Δ G_{1,2}

a fent mondottak miatt.

A Hold és a Nap együttes hatásának eredője együttállás esetén:

\begin{matrix} Δ G''_{1,2} = Δ G_{1,2} + Δ G'_{1,2} . \end{matrix}

A numerikus számítások eredményei:

A Nap terének gravitációs gyorsulása a Föld középpontjában

g_{f} = 5, 928 \cdot 10^{- 1} {cmsec}^{- 2}

, a Hold terében ugyanott:

g' = 3, 34 \cdot 10^{- 3} {cmsec}^{- 2}

, kb. 2 nagyságrenddel (100-szor) kisebb!

Az inhomogenitásból eredő gyorsuláskülönbség az 1-es és 0-ás helyzetek között a Nap terében:

g_{1,0} = 5, 069 \cdot 10^{- 5} {cm sec}^{- 2}

. Ugyanez a Hold terében:

g'_{1,0} = 1, 101 \cdot 10^{- 4} {cm sec}^{- 2}

, vagyis körülbelül kétszerese az előzőnek. A 0-ás és 2-es helyzetek között:

g_{0,2} = 4, 936 \cdot 10^{- 5} {cmsec}^{- 2}

, ill.

g'_{0,2} = 1, 08 \cdot 10^{- 4} {cm sec}^{- 2}

(szintén kb. kétszeres). A súlykülönbség az 1-es és 0-ás helyzetek között a Nap ill. Hold terében:

Δ G_{0,1} = 775

pond ill.

Δ G_{0,1} = 1685

pond. Ugyanez a 0-ás és 2-es helyzetek között:

Δ G_{0,2} = 756

pond, ill.

Δ G_{0,2} = 1651

pond. Súlykülönbség az 1-es és 2-es (déli és éjféli) helyzetek között a Nap hatására:

Δ G_{1,2} = 19

pond, a Hold hatására:

Δ G'_{1,2} = 34

pond. A Nap és Hold együttes hatására a keresett súlykülönbség:

Δ G''_{1,2} = 53

pond. A relatív súlykülönbség pedig mindössze:

Δ G''_{1,2} / G_{0} = 3, 53 \cdot 10^{- 9} = 3, 53 \cdot 10^{- 7} %

. Ugyanez a du. 6 órai és déli helyzetek között:

Δ G''_{1,0} / G_{0} = 1, 64 \cdot 10^{- 7} = 1, 64 \cdot 10^{- 5} %

. Látható, hogy a súlykülönbség miatt nem érdemes délben megvenni az árut és délután 6-kor eladni. A fenti eredményekből azt is leolvashatjuk, hogy a Holdnak nagyobb szerepe van az ár‐apály létrehozásában, mint a Napnak.

II. megoldás. Megmutatjuk, hogy a dinamika alapegyenleteinek segítségével hogyan lehet közvetlenül felírni a keresett súlyokat, majd a súlykülönbséget. Vizsgáljuk a jelenséget a Földhöz rögzített koordinátarendszerben. Meg kell jegyezni, hogy a Föld‐hajó egymáshoz rögzített rendszere gyorsuló koordinátarendszer, mivel a Nap terében centripetális erű hatására mozognak. Tudjuk, hogy a dinamika alapegyenletei (a Newton‐féle törvények) inerciarendszerben érvényesek, de ha bevezetjük az ún. tehetetlenségi, vagy inerciaerőket, akkor a valódi, vagy Newton‐féle erőkhöz ezeket hozzáadva, a gyorsuló koordinátarendszerben is ugyanúgy írhatjuk fel a dinamika törvényeit, mint inerciarendszerben (lásd a Matematikai Lapok XXI. kötet 3‐4. számában megjelent cikket a 161. lapon). Fel fogjuk írni a hajóra ható összes külső erők eredőjét, amelyről tudjuk Newton II. törvénye értelmében, hogy a test tömegének és gyorsulásának szorzatával egyenlő

(m a = \sum P_{k})

. A gyorsulást a választott koordinátarendszerünkhöz kell viszonyítanunk. A hajó gyorsulása a Földhöz képest nulla, tehát a hajó mozgásegyenlete a Földhöz rögzített koordinátarendszerben felírva:

m a = 0

. Írjuk fel a hajóra ható összes külső erőket. Ezek:

G_{0}

, a Föld hajóra gyakorolt vonzóereje (,,abszolút súlya''), a Napnak a hajóra gyakorolt vonzóereje (

P_{N h_{1}}

), a hajóra ható tehetetlenségi erő (

P_{1}

), végül a hajóra ható kényszererő (

P_{K_{1}}

), vagyis az az erő, amellyel a víz a hajót nyomja, ami nem engedi a hajót a Föld közepébe esni: a mindenkori, változó súly ellenereje. (Ezt mérhetjük a rugós erőmérővel.) Ezt keressük. (Hogy kényszermozgásra is érvényes legyen a

P = m a

törvény, a szabad erőkhöz hozzá kell venni a kényszererőket is, ekkor a törvény változatlan alakban érvényes.)
Számítsuk ki a mozgásegyenletből a súlyt délben. Mozgásegyenletünk: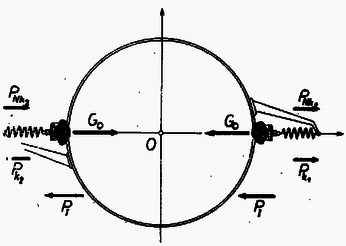

\begin{matrix} m_{h} a = G_{0} - P_{N h_{1}} + P_{1} - P_{K_{1}} = 0. \end{matrix}

Az erők előjelét irányuk határozza meg.

G_{0}

-t pozitívnak vettük mindkét esetben (l. a 3. ábrát).

3. ábra

Innen

\begin{matrix} P_{K_{1}} = G_{0} - P_{N h_{1}} + P_{1}, \end{matrix}

ahol

P_{1} = m_{h} R ω^{2}

centrifugális erővel, amit a gravitációs gyorsulással is kifejezhetünk:

P_{1} = m_{h} \cdot γ \frac{M}{R^{2}}

. (

R ω^{2}

a koordinátarendszer gyorsulása!) Ugyanez a mozgásegyenlet a 2-es helyzetre felírva így alakul:

\begin{matrix} m_{h} a = G_{0} + P_{N h_{2}} - P_{1} - P_{K_{2}} = 0, \end{matrix}

így

\begin{matrix} P_{K_{2}} = G_{0} + P_{N h_{2}} - P_{1} . \end{matrix}

Végül a keresett súlykülönbség:

\begin{matrix} Δ G_{1,2} = P_{K_{2}} - P_{K_{1}} = P_{N h_{1}} - 2 P_{1} + P_{N h_{2}} = γ m_{h} \cdot M (\frac{1}{{(R - r)}^{2}} - \frac{2}{R^{2}} + \frac{1}{{(R + r)}^{2}}) . \end{matrix}

Az eredmény azonos az első megoldáséval.
Láthatjuk, hogy a dinamika alaptörvényeit körültekintő módon alkalmazva biztos eszköz van a birtokunkban bonyolult, egyébként nehezen áttekinthető dinamikai problémák egyszerű megoldására.