Kezdőlap


Cím:	1961. évi fizika OKTV feladatai
Szerző(k):	Vermes Miklós
Füzet:	1961/október, 81 - 89. oldal	PDF \| MathML
Témakör(ök):	OKTV

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Az I. forduló feladatai:

1. A Földdel egyenlő átlagsűrűségű, homogén, de a Föld sugaránál

500

-szor kisebb sugarú égitesten mekkora maximális sebességgel közlekedhetnek a járművek ? Az égitest nem végez tengely körüli forgást. (A Föld sugara

6370 km

Megoldás: A megengedhető legnagyobb sebesség esetében a centripetális gyorsulás egyenlő a szabadesés gyorsulásával, vagyis

\frac{v^{2}}{r} = g

. Innen

v = \sqrt[]{r g}

. Ha

d

, a Föld sűrűsége adott, akkor

g = f \cdot \frac{4 π}{3} \cdot r^{3} \cdot d : r^{2} = \frac{4 π}{3} \cdot f d r

, (

f

tömegvonzási törvény állandója,

v

a sebesség,

r

az égitest rádiusza). Behelyettesítve a maximális sebesség képletébe:

v = r \sqrt[]{\frac{4 π}{3} \cdot f d}

. Ha a Földről van szó,

r = 6370 km

, és az átlagos sűrűség

5, 5 {g/cm}^{3}

, akkor

v = 7, 89 km/sec

, az első kozmikus sebesség. 500-szor kisebb rádiusz mellett a kritikus sebesség is 500-szor kisebb lesz, vagyis

15, 8 m/sec = 56, 88 km/óra

2. Vákuumban izzó

l

hosszúságú,

r

sugarú drótszálon

U

volt feszültségkülönbség mellett

I

amper erősségű áram folyik keresztül. A drótszál ekkor állandó hőmérsékleten izzik. A hővezetés elhanyagolható, és így a felvett teljesítmény hősugárzás formájában távozik a henger alakú drót palástján keresztül. Az

1 {cm}^{2}

felületen

1 sec

alatt kisugárzott hőmennyiség csak az izzószál hőmérsékletétől függ. Mekkorának kell választani a kétszeres hosszúságú, ugyanolyan anyagú drótszál sugarát, hogy az előbbivel egyező hőmérsékleten való izzásnál a felvett teljesítmény is megegyezzék az előbbivel ? Mekkora ez esetben a kétszeres hosszúságú szál végei között a feszültségkülönbség ?

Megoldás: Minthogy a második drótszál esetében ugyanakkora teljesítménynek kell eltávoznia ugyanazon a hőmérsékleten, ezért a második drót hengerpalástjának a felszíne egyenlő kell hogy legyen az első drót palástfelszínével. A palást felszíne egyenesen arányos a rádiusszal és a hosszal

(2 π r l)

, ezért a hosszúság megkétszerezése a rádiusz megfeleződését vonja maga után, így a második drót rádiusza az első drót rádiuszának a fele. A második drót ellenállása

(R)

az elsőnek 8-szorosa, mert a teljesítmény

U^{2} : R

, így 8-szor nagyobb

R

esetében 8-szor nagyobb

U^{2}

szükséges. Tehát a szükséges feszültségkülönbség

\sqrt[]{8} = 2 \sqrt[]{2}

-ször nagyobb az eredetinél.

3. Vízszintes lapon hasábalakú test fekszik egyik lapján. A hasáb két ellentétes oldalához egy-egy rugalmas szálat erősítünk. Mindkét rugalmas szál teljesen egyforma, és egy egyenesbe esik. Az alaphelyzetben mindkét szál feszítetlen állapotban van. Ha a testet a szálak egyenesében oldalt kimozdítjuk, akkor elengedés után a test rezgő mozgásba jön. Hogyan csökken az amplitúdó, ha a rezgést csupán a testnek a vízszintes síkon való súrlódása csillapítja ? Ha a testet indításkor

s_{0} = 3, 8 cm

-rel térítettük ki nyugalmi helyzetéből, akkor hány lengés után és hol áll meg ? A test tömege

2 kg

. Akármelyik rugalmas szálat

1 kp

erő

2 cm

-rel nyújtja meg. A súrlódási együttható

0, 2

Megoldás: Vizsgáljuk a hasáb alakú test középpontjának mozgását, először súrlódás nélkül. A rugalmas fonalak jelenléte azt jelenti, hogy az úttal arányos visszavivő erő működik, amely rezgő mozgást okoz. Ennek útja, sebessége ereje:

\begin{matrix} s = s_{0} \cdot sin ω t, \\ v = ω s_{0} \cdot cos ω t, \\ P = - m ω^{2} s . \end{matrix}

Itt

t

az idő,

ω = \frac{2 π}{T}

, ahol

T

a teljes rezgésidő. A tömeg a mi feladatunkban

m = 2000

gramm. Az ún. rugóállandó, amelyaz 1 cm-es úthoz tartozó visszavivő erőt jelenti:

D = \frac{P}{s} = 490 000 din/cm

. A rezgés törvénye szerint

\begin{matrix} T = \frac{2 π}{ω} = 2 π \sqrt[]{\frac{s m}{P}} = 2 π \sqrt[]{\frac{m}{D}} = 0, 4 sec, azonkívül ω = \sqrt[]{\frac{D}{m}} = 15, 5 {sec}^{- 1} . \end{matrix}

Ábrázoljuk egy koordinátarendszer vízszintes tengelyén az utat és a függőleges tengelyen a testre ható erőt (1. ábra).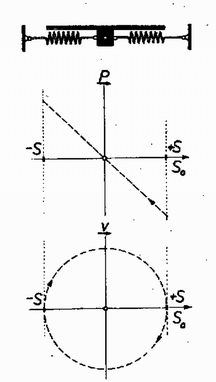

1. ábra

Az origót a rezgő pont nyugalmi helyzetébe tesszük. A jobbra vívó erőt tekintjük pozitívnak. Az erő grafikonja süllyedő egyenest ad, hiszen az erő arányos a nyugalmi helyzettől mért távolsággal, és visszaviszi a tömeget nyugalmi helyzetébe:

P = D s

.
Vizsgáljuk a sebesség függését az úttól. A sebességtörvényből

\frac{v}{ω} = s_{0} \cdot cos ω t

, ennek a négyzetét és az út négyzetét összeadva

\begin{matrix} s^{2} + {(\frac{v}{ω})}^{2} = s_{0}^{2} \cdot sin^{2} ω t + s_{0}^{2} \cdot cos^{2} ω t = s_{0}^{2}, \frac{v}{ω} = \sqrt[]{s_{0}^{2} - s^{2}}, v = ω \sqrt[]{s_{0}^{2} - s^{2}} . \end{matrix}

Ez a képlet adja meg, hogy a rezgő mozgásnál hogyan függ a sebesség az úttól; grafikus ábrázolása ellipszis. Gyakorlati, kényelmi okokból nem

v

sebességgel, hanem

\frac{v}{ω}

-val foglalkozunk. A

V = \frac{v}{ω}

értéket redukált sebességnek nevezzük; ennek ismerete a tényleges sebességet is megadja, hiszen

v = ω V

, vagyis a redukált sebességet szögsebességgel megszorozva megkapjuk a tényleges sebességet. Az 1. ábrán egy második, alsó koordinátarendszerben a redukált sebességnek az úttól való függését ábrázoljuk:

\begin{matrix} V = \sqrt[]{s_{0}^{2} - s^{2}} . \end{matrix}

Az ábrázolás kört ad.
Kísérjük végig a mozgás lefolyását a súrlódás nélküli esetben. Pozitív (jobboldali)

s_{0} = 3, 8 cm

-es helyzetből engedjük el a testet. Rezgés indul meg

s_{0}

amplitúdóval, közben az erőt a ferde egyenesen, a sebességet a körön mozgó pont helyzete tünteti fel.
Most vizsgáljuk meg a súrlódás szerepét. A súrlódási erő fellép, amint sebességkülönbség, relatív sebesség van a hasáb alakú test és az alatta levő vízszintes felület között. Feltételezésünk szerint a súrlódási erő független a sebességtől. A súrlódási erő a mozgató erő abszolút értékét csökkenti, függetlenül az iránytól. A hasáb alakú testet

m g

súlya nyomja a felszínhez, ezért a súrlódási erő

P_{s} = μ m g = 392 000 din

, (

μ = 0, 2

a súrlódási együttható). A súrlódási erő a felület minden helyén ugyanakkora, viszont a hasábra ható rugalmas fonálerő az origóban nulla, onnan kilépve az origótól mért távolsággal egyenes arányban növekszik. Egy bizonyos távolságban (

s_{s}

) egyenlővé válik a súrlódási erő és a rugalmas fonálerő (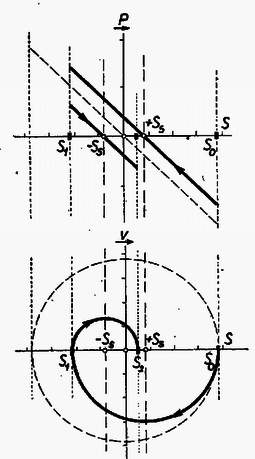

P = D s

\begin{matrix} P_{s} = D s_{s} . Innen: s_{s} = \frac{P_{s}}{D} = 0, 8 cm . \end{matrix}

Ez az

s_{s}

mennyiség, a súrlódási határ igen fontos szerepet tölt be. Ha a tárgyat

\pm s_{s}

nyugalmi határon belül tesszük rá a felületre (például az origóba, az origótól

0, 2

cm,

0, 5

cm stb. távolságba) akkor ott marad azon a helyen, mert az

s_{s}

határon belül nagyobb a súrlódási erő, mint a rugalmas erő, és a rugók, nem képesek elhúzni a testet. A rátevés nyugalomban való rátevést jelent. Ha az

s_{s}

határokon kívül tesszük a hasábot a felületre, akkor elengedés után valamerre elmozdul, mert az

s_{s}

határokon kívül nagyobb a rugalmas erő, mint a súrlódási erő.

2. ábra

Ezután vizsgáljuk meg a mozgás lefolyását súrlódás jelenlétében. Elkészítjük koordináta-rendszereinket, amelyek

P

erőnek és

V

redukált sebességnek az úttól való függését tüntetik fel (2. ábra), és bejelöljük kétoldalt az

s_{s}

, súrlódási határokat. A szaggatott ferde egyenes és a kör a súrlódás nélküli, már megtárgyalt esetre vonatkoznak. A tárgyat

s_{0} = + 3, 8 cm

távolságban helyezzük rá a felületre és elengedjük. Ekkor megkezdi mozgását. A balra húzó rugóerő nagyságát minden pontban csökkenti a súrlódási erő, a ládát csak

P - P_{s} = D s - D s_{s}

erő mozgatja balfelé. Ennek ábrázolása

+ s_{s}

-en átmenő egyenes (amely párhuzamos a súrlódás nélküli eset egyenesével).

+ s_{s}

-ben a hasáb erőmentes. Ezután a súrlódás tovább fékez, majd a negatív oldalon fékező hatása hozzáadódik a rugó fékező erejéhez. Most is rezgés keletkezik, de ennek középpontja

+ s_{s}

, mert a testre ható erő az ettől mért távolsággal egyenesen arányos. A rezgés

+ s_{s}

-től mért amplitúdója

s_{0} - s_{s} = 3 cm

.
A sebességre is érvényes, hogy

+ s_{s}

körüli rezgő mozgásról van szó. A redukált sebességet

+ s_{s}

körül rajzolt,

s_{0} - s_{s}

rádiuszú félkör ábrázolja.
A rezgő pont a negatív (bal) oldalon az origótól mérve

s_{1}

amplitúdóig lendül ki. Minthogy az

s_{0} - s_{s}

amplitúdó

+ s_{s}

-től mérendő,

s_{1} = s_{0} - 2 s_{s} = 2, 2 cm

.
Tehát a jobb oldalon

s_{0}

ból indult tárgy a baloldalon

s_{1}

-ig lendült ki. Ez a pont a mi példánk esetében kívül van az

s_{s}

súrlódási határon, itt a rugó erősebb, mint a súrlódás, és a hasáb megindul visszafelé. A rugalmas erőből ismét levonandó a súrlódási erő, és olyan rezgő mozgás keletkezik, amelynek

- s_{s}

a középpontja; a hatóerőt a

- s_{s}

ponton átmenő ferde egyenes ábrázolja. E mozgás

- s_{s}

-től mért amplitúdója

s_{1} - s_{s} = 1, 4 cm

. Ilyen messzire megy

- s_{s}

-től jobbfelé is, jobboldalt az origótól mérve

s_{2} = s_{1} - 2 s_{s} = 0, 6 cm

az amplitúdó. Ami a sebességet illeti, visszamenéskor a redukált sebességet

- s_{s}

körül rajzolt

s_{1} - s_{s}

rádiuszú félkör tünteti fel.
Rezgő tömegünk átjutott az origó jobboldalára, és

s_{2} = 0, 6 cm

távolságban megállt. Ez a hely a

\pm s_{s}

zónán belül van, ahol nagyobb a súrlódási erő, mint a rugalmas erő, ezért a test itt marad, a felületéhez tapadva.
A feladat megoldása: rezgő mozgás megy végbe, de

+ s_{s}

és

- s_{s}

középpontok körül. Az amplitúdó számtani sor szerint csökken, minden fél lengés, egy ide vagy oda menés alkalmával

2 s_{s}

-sel lesz kevesebb. Ez mindaddig tart, amíg a test valamely féllengését befejezve a

\pm s_{s}

zónán belül áll meg, mert ekkor ezen a helyen marad megállva, ott ragadva. A mi esetünkben két féllengés után

+ 0, 6 cm

-en állt meg a test.
Megoldható a feladat az energiaelv alapján is. A nyugalmi helyzettől

s

távolságban a rugalmas helyzeti energia

0, 5 D s \cdot s = 0, 5 D s^{2}

, mert

s

távolságban az erő

D s

, a munkavégzés állandó erő mellett

D s \cdot s

volna, de mivel az erő lineárisan csökken, középértékben a fele számít. Ha

s_{0}

távolságban indítjuk el a tömeget, akkor kiindulási helyzeti energiája egyenlő az

s

távolságban még meglevő helyzeti energia, a megszerzett mozgási energia és a súrlódási erő ellen végzett munka összegével:

0, 5 D s^{2} = 0, 5 D s^{2} + 0, 5 m v^{2} + (s_{0} - s) μ m g

.
Ezen az alapon is eljuthatunk ugyanezekhez az eredményekhez.

A II. forduló feladatai:

1. Vízszintes sínen kocsi gurul. Ha a kocsi sebessége a súrlódás következtében

10 m/sec

-ra csökken, a kocsiból a kocsi mozgásával ellentétes irányban lövedéket lőnek ki, amelynek repülési sebessége a talajhoz viszonyítva mindig

c = 1700 m/sec

. Ezáltal a kocsi ismét eredeti sebességére gyorsul. A kocsiból félpercenként lőnek ki lövedékeket, az egymás után kirepülő lövedékek tömege mindig kisebb és kisebb. A

200

-adik lövedék tömege éppen tizede az első lövedék tömegének. Ha a kocsi mozgását csak a súrlódás fékezi, mekkora a súrlódási együttható ? (A kilövés ideje elhanyagolhatóan kicsiny.)

Megoldás: A kocsi eredeti tömege (valamennyi lövedékkel együtt)

M

, az egyes lövedékek tömegei

m_{1}, m_{2}, ...

. Az eredeti és minden lövés után újra létrejövő sebesség

v_{0}

, a lövés pillanata előtt a lelassult sebesség

v = 10 m/s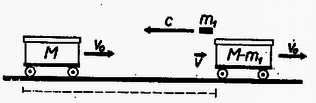ec

. (3. ábra).

3. ábra

Alkalmazzuk az impulzustételt az első lövedék kilövésére. A kilövés előtti impulzus

M v

, a kilövés után a lövedék impulzusa

- m_{1} c

, a kocsi megmaradt részéé

(M - m_{1}) v_{0}

. Ezért:

\begin{matrix} M v = (M - m_{1}) v_{0} - m_{1} c . \end{matrix}

Rendezve:

\begin{matrix} \frac{m_{1}}{M} = \frac{v_{0} - v}{v_{0} + c} = k . \end{matrix}

(1)

A jobboldal értéke minden kilövésnél ugyanaz, mert a benne szereplő mindhárom sebesség mindig ugyanaz. Tehát az eredeti sebesség helyreállításához szükséges kidobandó tömeg és a kidobás előtti összes tömeg hányadosa mindegyik kilövésnél ugyanannyi.
Számítsuk ki az egymás után kidobandó tömegeket:

\begin{matrix} m_{1} = k M, \\ m_{2} = k (M - m_{1}) = k (M - k M) = k M (1 - k), \\ m_{3} = k (M - m_{1} - m_{2}) = k (M - k M - k M + k^{2} M) = k M (1 - 2 k + \\ + k^{2}) = k M {(1 - k)}^{2}, ... \end{matrix}

Mivel a sorozatot bármelyik kilövésnél elkezdhetjük, bebizonyosodott, hogy a lövedékek tömegei mértani sort alkotnak, melynek első tagja

k M

, hányadosa

1 - k

. Az

n

-ik lövedék tömege:

\begin{matrix} m_{n} = k M {(1 - k)}^{n - 1}, \end{matrix}

ennek hányada az első lövedék tömegéhez,

m_{1} = k M

-hez viszonyítva:

\begin{matrix} \frac{m_{n}}{m_{1}} = {(1 - k)}^{n - 1} . \end{matrix}

(2)

A fékeződést a súrlódás okozza, a súrlódási erő

μ m g

, a súrlódás által okozott negatív gyorsulás

μ g

; egyenletesen lassuló mozgás jön létre, amelynél a sebesség csökkenése egyik lövéstől a másikig

v_{0} - v = μ g T

. Tehát:

\begin{matrix} v_{0} = v + μ g T . \end{matrix}

(3)

(

μ

a súrlódási együttható,

g

az esés gyorsulása,

T

az egyes lövések között eltelt idő.)
Felhasználjuk a sebességcsökkenésre kapott ezen eredményünket.
Először (1) alapján

1 - k

\begin{matrix} 1 - k = 1 - \frac{v_{0} - v}{v_{0} + c} = \frac{v + c}{v_{0} + c}, \end{matrix}

(3)

ide pedig (3) értékét helyettesítve:

1 - k = \frac{v - c}{v + c + μ g T}

.
Ezt pedig (2)-be helyettesítjük:

\frac{m - n}{m_{1}} = {(\frac{v + c}{v + c + μ g T})}^{n - 1}

.
Innen kifejezzük az ismeretlen

μ

súrlódási együtthatót:

\begin{matrix} μ = \frac{v + c}{g T} \cdot [\sqrt[^{n - 1}]{\frac{m_{1}}{m_{n}}} - 1] . \end{matrix}

Feladatunk számértékei szerint

T = 30 sec

v = 10 m/sec

c = 1700 m/sec

n = 200

m_{1} : m_{n} = 10

; ezek alapján

\begin{matrix} μ = 0, 0675 = 6, 75 % . \end{matrix}

A súrlódási együtthatót ismerve kiszámítható az eredeti sebesség:

v_{0} = 29, 77 m/sec

, valamint a kocsi útja az egyes lövések között:

s = v_{0} T - 0, 5 μ g T^{2} = 596, 55 m

.
A lövedéktömegek mértani sorának hányadosa:

1 - k = 0, 9886

. A feladatból csak a tömegek arányai derülnek ki, az első lövedék tömege

0, 0114

M, az utolsóé

0, 00114

M, a lövedékek együttes tömege

0, 8992

M, a kocsi megmaradt tömege a végén

0, 1008

50 cm

hosszú cső egyik végén

2

dioptriás gyűjtő, másik végén

- 2

dioptriás szórólencse van. A szórólencse mögött a szórólencsétől

x

távolságra a cső tengelyére merőleges síktükröt helyezünk el. Mekkora

x

mellett lehetséges, hogy a gyűjtőlencse előtt a lencsétől

100 cm

távolságra elhelyezett tárgy valódi képe a tárgy síkjában keletkezzék? Mekkora a nagyítás, és milyen állású a kép?

Megoldás: A szórólencse a gyűjtőlencse fókuszában van (4. ábra).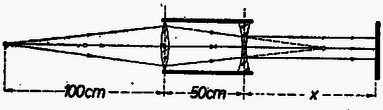

4. ábra

A gyűjtőlencsétől 100 cm távolságban, a tengelyben egy fénylő pontot helyezünk el. Mivel ez a tárgypont a kétszeres fókusztávolságban van, képe ugyancsak a kétszeres fókusztávolságban keletkezik, 50 cm-rel jobbra a szórólencsétől. Ez a pont a szórólencse fókusza, ezért a feléje tartó sugárnyaláb párhuzamosan hagyja el a szórólencsét. Bárhol legyen is a síktükör, a feléje menő sugárnyaláb önmagában tér vissza kiindulási helyére. Ezzel feleltünk az első kérdésre.
A második kérdésre úgy tudunk válaszolni, hogy a tárgypontot a tengelyen kívül helyezzük el. Most a szórólencsét párhuzamosan elhagyó sugárnyaláb ferdén felfelé halad, visszaverődik a síktükrön, és ferdén felfelé haladva újra átmegy a szórólencsén. A szórólencse után szétterjedve halad a sugárnyaláb, mintha a szórólencse gyújtósíkjának egy pontjából indulna ki. Ezt a pontot képezi le a gyűjtőlencse (5. ábra).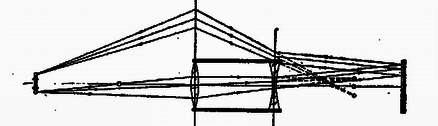

5. ábra

Az eredmény: a kép reális, a tárgy helyén keletkezik, eredeti nagyságú és fordított helyzetű. A rajz figyelmeztet arra, hogy ilyen berendezés csak igen szűk sugárnyalábot képes átengedni, csak a tengelyhez nagyon közel fekvő pontokat képes leképezni.

3. Egyik végén átfúrt súlytalan merev rudat egy motor vízszintes tengelyére húzunk, a rúd másik végén pontszerű súlyos test van. Ha a rudat kilendítjük egyensúlyi helyzetéből, függőleges síkban ingalengéseket végez. Tegyük fel, hogy ezen inga lengéseit csak a tengelynél fellépő súrlódás csillapítja. A súrlódási együttható a sebességtől független állandó. a) Mikor csillapodik gyorsabban az inga lengése, ha a tengely áll, vagy ha forog ? Miért ? b) Lehetséges-e, hogy ha a tengely forog, az inga csillapítatlan lengést végez ? Ha igen, milyen összefüggés van ez esetben a legnagyobb kitérés szöge és a tengely fordulatszáma között ? (Feltéve, hogy az inga csak kis tágasságú lengéseket végez.)

Megoldás: Az eset vizsgálatát az I. forduló 3. feladatához kapcsoljuk. Ott arról volt szó, hogy egy rugalmas fonalak közé akasztott test vízszintes felületen rezgő mozgást végez, amelyet a súrlódás csillapít. Ezt a feladatot úgy általánosítjuk, hogy a test nem nyugalomban levő felületen, hanem egyenletes sebességgel, állandóan mozgó felületen végzi rezgését, például egy transzmissziós szalagon (6. ábra).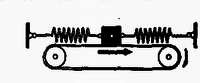

6. ábra

Első esetben legyen a szalag sebessége nagyobb, mint a rezgés folyamán előforduló bármely sebesség. A szalag mozogjon pozitív irányban, balról jobbra

C

redukált sebességgel. (Legyen például

C = 4 cm

, vagyis

c = ω C = 62 cm/sec

). A tárgyat jobboldalról,

s_{0} = 3, 8 cm

-ről engedjük el. A rezgés első felében a súrlódási erő mindig a rugalmas erő ellen dolgozik, fékez. A mozgás olyan, mintha

+ s_{s}

középpont körül

s_{0} - s_{s} = 3 cm

amplitúdóval menne végbe rezgés, és a test a baloldalon

s_{1} = 2, 2 cm

amplitúdóig lendül ki,

s_{1} = s_{0} - 2 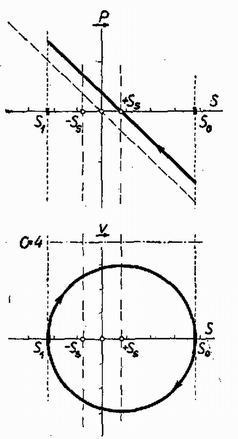s_{s}

(7. ábra).

7. ábra

Ezután a test elindul visszafelé, de most egészen más az eset, mint az első féllengés folyamán. Visszamenet a szalag a mozgás irányában halad, a súrlódási erő előre viszi a tárgyat, segít a visszahúzó rugalmas fonálnak. A testre ható erő a rugalmas erő és a súrlódási erő összege. Az erő diagramja most is

+ s_{s}

-en átmenő egyenes. Ez így van a visszamenés egész tartama alatt, hiszen a szalag mindig gyorsabb, mint a test, így a súrlódási erő állandóan előre, jobbra akarja vinni a testet. Csillapítatlan rezgés keletkezik, középpontja

+ s_{s}

, amplitúdója innen mérve

s_{0} - s_{s}

. A sebességdiagram kör, ennek középpontja

+ s_{s}

, rádiusza redukált sebességben

s_{0} - s_{s} = 3 cm

. Annak feltétele, hogy az itt tárgyalt módon csillapítatlan rezgés keletkezzék az, hogy a rezgés folyamán létrejövő sebesség sohase legyen nagyobb, mint a szalag sebessége:

\begin{matrix} s_{0} - s_{s} \leq C . \end{matrix}

(4)

A feltételt redukált sebességgel írtuk fel;

s_{0} - s_{s}

a rezgés folyamán előforduló legnagyobb redukált sebesség.
Ha a tárgyat baloldalról indítjuk, ugyanez történik:

+ s_{s}

körül csillapítatlan rezgés keletkezik. Ha a baloldali, középtől mért amplitúdót

s_{0}

-al jelöljük, akkor a

+ s_{s}

-től mért amplitúdó

s_{0} + s_{s}

, és az előbbi feltétel így szól:

\begin{matrix} s_{0} + s_{s} \leq C . \end{matrix}

Második esetben legyen a szalag sebessége kisebb értékű, akkora, hogy a tárgy sebessége időnként lépje túl a szalag sebességét. Példánkban

C = 3 cm

legyen a szalag redukált sebessége, és indítsuk a tárgyat baloldalról,

s_{0} = 3, 8 cm

-ről. A nulla sebességgel induló, lassan gyorsuló hasábot a szalag eleinte húzza, mert a szalag sebessége gyorsabb, mint a tárgyé, és a súrlódási erő hozzáadódik a rugalmas erőhöz. Az erő grafikonja a

+ s_{s}

-en átmenő egyenessel kezdődik (8. ábra).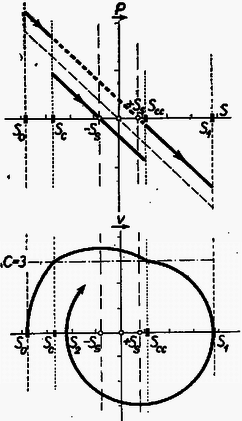

8. ábra

Ugyanekkor a sebesség növekedését

s_{0}

-ból kiinduló,

+ s_{s}

középpontú,

s_{0} + s_{s}

rádiuszú körív adja. Azonban egy bizonyos pontban, amikor ez a körív metszi a mozgó szalag

C

redukált sebességét jelentő egyenest, a mozgó test sebessége eléri a szalag sebességét. Ez balra az origótól

s_{c} = 2, 7 cm

távolságban következik be. Tovább mozogva a mozgó szalag fékezi a mozgást, mert lassabb, és ettől kezdve a súrlódási erő levonódik a rugalmas erőből.

s_{c}

-től kezdve a hatóerőt jelentő pont a

- s_{s}

-en átmenő egyenesen halad, a sebességet pedig olyan körív adja meg, amelynek

- s_{s}

a középpontja, és amely az előbbi körívhez csatlakozik. Ez a mozgásállapot

s_{c c} = 1, 1 cm

-ig tart, ahol ez a második körívünk újra metszi

C

egyenesét. Ettől kezdve megint a szalag a gyorsabb, előrehúzza a tárgyat, és a súrlódási erő algebrailag hozzáadódik a rugalmas erőhöz. Az erőt ábrázoló pont ismét a

+ s_{s}

-en átmenő egyenesen halad. A sebesség értékeit úgy kapjuk meg, hogy

+ s_{s}

-be leszúrt körzővel olyan körívet rajzolunk, amely

C

magasságában csatlakozik a második körívhez. A sebesség

s_{1} = 3, 9 cm

-nél lesz nulla, a tárgy eddig jut el jobboldalt. Azután elindul vissza, miközben a súrlódás mindvégig fékezi, mert a szalag szembe szalad. Ekkor a sebességdiagram

+ s_{s}

középpontú,

s_{1} - s_{s} = 3, 1 cm

rádiuszú félkör, az erőt ábrázoló pont a

+ s_{s}

-en átmenő egyenesen halad. Újra balra átlendülve

s_{2} = 2, 3 cm

-ig jut el balra. Ezután az adatoktól függ, nevezetesen a (4) feltétel teljesülésétől, hogy az első eset szerinti csillapítatlan, vagy a második eset szerint kissé csillapodó lesz-e a mozgás. Előbb-utóbb annyira csillapodik a rezgés, hogy a (4) feltétel teljesül, és azután már csillapítatlan a rezgés.
Adódhatnak érdekes, különleges esetek is. Ha példánk adatai mellett a mozgó szalag redukált sebessége

C = 4, 4 cm

, akkor a

+ s_{s}

középpontból rajzolt körív

s_{c} = 0, 5 cm

-nél; a

\pm s_{s}

zónán belül metszi

C

egyenesét (9. ábra).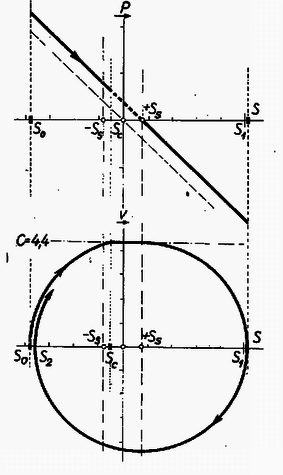

9. ábra

Innentől kezdve megszűnik a szalag gyorsító hatása, mert már nem gyorsabb, mint a rezgő test. De a

\pm s_{s}

zónán belül vagyunk, ahol a súrlódási erő nagyobb, mint a rugalmas erő. A rugalmas fonalak nem képesek a tárgyat a szalagon odébb rántani, a tárgy odatapadva a szalaghoz a szalag sebességével (0 teljes hatóerő mellett) halad

+ s_{s}

-ig. Ezután szóhoz jut a rugalmas erő, a tárgy egy rezgőmozgás negyedperiódusát végzi el

+ s_{s}

mint középpont körül

s_{1} = 5, 2 cm

szélső amplitúdóig. Visszafelé a sebesség alakulását az utolsó körív folytatása adja meg egészen

s_{2} = - 3, 6 cm

-ig, sőt azután is, mert most már teljesül a (4) feltétel.
Egy másik érdekes lehetőség következik be például

C = 3, 5 cm

redukált sebességnél (10. ábra).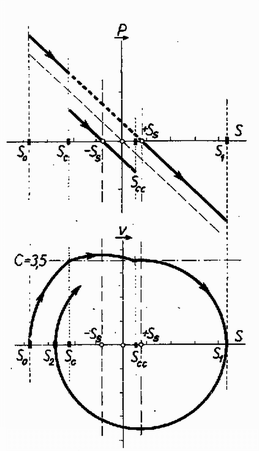

10. ábra

A sebesség körívének első metszése

s_{c} = - 2, 2 cm

-nél következik be. Ekkor átkerül a sebességkör középpontja

- s_{s}

-be, és így folytatódik a sebességdiagram a második körívvel. Most a mozgó test sebessége gyorsabb, mint a szalagé, és a súrlódás fékez. De

s_{c c} = 0, 6 cm

-nél a második körív újra metszi

C

egyenesét, méghozzá

\pm s_{s}

határon belül. Ez azt jelenti, hogy

+ s_{s}

-ig viszi a szalag a tárgyat, mint előbb. A sebességdiagram

+ s_{s}

középpontú körrel folytatódik, most már mindvégig.
Nyilvánvaló, ezzel a gondolatmenettel teljesen elintéztük a II. forduló 3. feladatát, hiszen ebben az ingaszerkezet olyan berendezést jelent, amely nagy közelítéssel a nyugalmi helyzettől mért távolsággal arányos visszavivő erőt hoz létre, a tengely súrlódó felülete pedig egyirányban mozgó súrlódó felületet jelent. Tehát abban az esetben, ha a lécen levő furat belső felszínén levő pontok lengési sebessége nem lépi túl a tengely felszínén levő pontok mozgási sebességét, azonnal csillapítatlan rezgés keletkezik, hanem így van, akkor egy-két csillapodó lengés után következik be ez az állapot. A (4) feltétel teljesülését mennyiségileg csak akkor lehet megvizsgálni, ha tudnánk, mekkora rugalmas erők szorítják a lécet a tengelyhez, vagy olyan laza-e a furat, hogy csak a léc súlyából származik súrlódás. Ismernünk kell a súrlódási együttható nagyságát is.

Az 1961. évi országos középiskolai tanulmányi versenyen fizikából I. díjat nyert Szegi András, a Budapest, II. kerületi II. Rákóczi Ferenc g. III. o. tanulója, II. díjat nyert Perjés Zoltán a Budapest, VIII. kerületi Piarista g. IV. o. tanulója, III. díjat nyert Góth László, a Budapest, IV. kerületi Könyves K. g. III. o. tanulója. Dicséretet és könyvjutalmat nyertek a következő tanulók: Bácsy Zsolt (Bp., V. Eötvös g.), Bollobás Béla (Bp., V. Apáczai Cs. g.), Dömötör Gyula (Szeged, Radnóti g.), Frint Gábor (Mosonmagyaróvár, Kossuth L. g.), Kiszely György (Bp., VIII. Piarista g.), Kóta Gábor (Tatabánya, Árpád g.), Molnár Emil (Győr, Révai g.), Pellionisz András (Bp., V. Apáczai Cs. g.), Somogyi Károly (Bonyhádi g.), Szegő Károly (Bp., V. Apáczai Cs. g.), Temesvári Gyula (Bp., II. Toldy g.), Zakariás László (Bp., VIII. Piarista g.).