Kezdőlap


Cím:	Bonyolultabb áramköri problémák megoldása a Kirchhoff-tételek segítségével
Szerző(k):	Horváth Péter
Füzet:	1961/április, 177 - 179. oldal	PDF \| MathML
Témakör(ök):	Szakmai cikkek

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Ohm törvénye és a Kirchhoff tételek segítségével sok egyszerű áramköri problémát lehet megoldani. Alkalmaztuk ezeket párhuzamosan kötött ellenállások esetén, shunt és előtét ellenállások méretezésekor. A következőkben megmutatjuk, hogy általánosabb megfogalmazásban bonyolultabb áramkörök számítására is alkalmasak.
I. Egy áramkör valamely szakaszán a feszültségesés egyenlő az ellenállásnak és a szakaszon átfolyó áramok algebrai eredőjének szorzatával (Ohm) törvénye).

\begin{matrix} E_{i} = R_{i} \sum_{k}^{} I_{i k} \end{matrix}

II. A vezetékhálózat egy csomópontjába érkező és az onnan eltávozó áramok algebrai összege zérus (Kirchhoff I.).

\begin{matrix} \sum_{n}^{} I_{n} = 0 \end{matrix}

III. A vezetékhálózatban bármely zárt kör mentén a feszültségesések összege egyenlő az elektromotoros erők összegével (Kirch. II.).

\begin{matrix} \sum_{k}^{} R_{k} \cdot I_{k} = \sum_{k}^{} E_{k} . \end{matrix}

A tételek megengedik több áramforrás használatát, érvényességük viszont egyenáramokra korlátozódik. I. fenti megfogalmazása azt is jelenti, hogy az ellenállás független az áramintenzitástól; a hálózat lineáris.
Főként a harmadik tétel megfogalmazása tér el az eddigiektől. Egy áramkörre minden további nélkül érthető. Más szavakkal lényegében az első tételt fejezi ki. Bonyolultabb vezetékhálózatban szintén az Ohm törvény érvényét terjeszti ki a hálózatban kiszemelt tetszőleges zárt vezetőkörre.
Egy vezetékhálózatra vonatkozólag, ha ismerjük az elektromotoros erőket és az ellenállásokat, a fenti tételek pontosan annyi független egyenletet adnak, ahány az

n

ághoz tartozó

2 n

ismeretlen adat (feszültségesések és áramok) meghatározásához szükséges.
Hogy ezt belássuk, tekintsük az 1. ábrán látható vezetékhálózatot, amelynek minden köre csak három ágból áll, és csak külső, a hálózat kontúrján elhelyezkedő csomópontokat tartalmaz. A külső ágak száma egyenlő a csomópontok számával, az egyes körök közös, belső ágainak száma pedig eggyel kevesebb a körök számánál.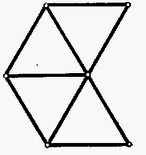

1. ábra

Ha most egy tetszőleges ágon felveszek egy újabb csomópontot, akkor ezzel az ágat két részre bontottam, ha pedig ezt a csomópontot egy másikkal, egy új ággal összekötöm, akkor egy áramkört bontottam két részre. Tehát a csomópontok vagy a körök számának növelése az ágak számának ugyanakkora növekedését eredményezi.
Ilyen eljárással tetszőleges vezetékhálózat állítható elő, ezért általában mondhatjuk, hogy egy

l

áramkört és

m

csomópontot tartalmazó hálózatban

n = m + l - 1

ág van.
A csomóponti tétel

m - 1

független összefüggést, az áramköri tétel

l

egyenletet ad. Ehhez járul még az Ohm törvény

n

egyenlete, tehát a

2 n

ismeretlen meghatározására ugyanannyi független egyenletünk van.
Az egyenletek megoldására kétféle módszer használható. Ezeknek lényege az, hogy csak az egyik Kirchhoff tétel egyenleteit írjuk fel olyan alakban, hogy azzal a másik tétel egyenleteit már ki is elégítettük. Így az egyenletek száma csökken, a számolás egyszerűbb lesz. A továbbiakban olyan áramkörökkel foglalkozunk, melyeknél Kirchhoff II. tételét alkalmazhatjuk. A tétel alkalmazása könnyebb, viszont csak síkban kiteríthető hálózatok esetén használható.
A 2. ábrán látható áramkör adatait

R_{1}

R_{2}

R_{3}

ellenállásokat és

E_{1}

E_{2}

elektromotoros erőket ismerjük. Kiszámítandó, mekkora áramok folynak az egyes ágakban, mekkorák a feszültségesések az ellenállásokon.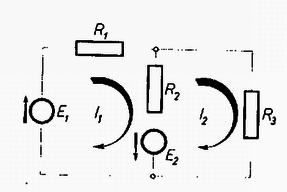

2. ábra

Minden zárt áramkörben felveszünk

I_{1}

I_{2}

I_{3}

...

I_{n}

áramokat. (Jelen esetben

I_{1}

I_{2}

.) A kezdeti irányítás tetszőleges, pl. az óramutató járásával megegyező irányú. Az előjelviszonyok majd megadják a valódi irányokat. Az egyértelmű irányítás azonban elengedhetetlen.
Belátható, hogy ezekkel a köráramokkal a II. tételt ki is elégítettük. A III. egyenletek felírása előtt jegyezzük meg, hogy a körök közös ágaiban mindig két áram különbsége folyik, tehát pl.

R_{2}

-n

I_{1} - I_{2}

lefelé. Figyelni kell arra is, hogy a generátorok irányítottak, és ezeket is megfelelő előjellel kell tekintetbe venni.
Tehát a III.-t az első körre alkalmazva:

\begin{matrix} E_{1} + E_{2} = (R_{1} + R_{2}) I_{1} - R_{2} I_{2} \end{matrix}

(1. a)

és a második körre:

\begin{matrix} - E_{2} = - R_{2} I_{1} + (R_{2} + R_{3}) I_{2} . \end{matrix}

(1. b)

Azért szerepel

- E_{2}

, mert a generátor irányítása

I_{2}

-vel ellentétes. Ez két egyenlet két ismeretlennel.

I_{1}

és

I_{2}

kiszámítása után minden adat rendelkezésre áll.
Egy további példán vizsgáljuk meg a módszer alkalmazhatóságát. A 3. ábrán a Wheatstone‐híd kapcsolási rajza látható. A jelölések ismertek

R_{b}

és

r_{b}

a galvanométer ill. a telep belső ellenállása. A hálózat három körből áll. Ezekben

I_{1}

I_{2}

I_{3}

áramok folynak az óramutató járásával megegyező irányban.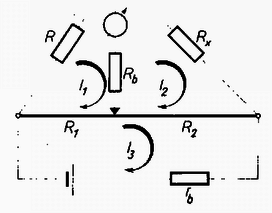

3. ábra

Alkalmazva a III-t:

\begin{matrix} 0 = I_{1} (R + R_{1} + R_{b}) - I_{2} R_{b} - I_{3} R_{1} & (2.a) \\ 0 = - I_{1} R_{b} + I_{2} (R_{x} + R_{2} + R_{b}) - I_{3} R_{2} & (2.b) \\ E = - I_{1} R_{1} - I_{2} R_{2} + I_{3} (R_{1} + R_{2} + r_{b}) . & (2.c) \end{matrix}

Először tisztázzuk az egyensúly feltételét. Hogy a számításokat egyszerűbbé tegyük, legyen

R_{b}

és

r_{b} ≪ R_{1}

R_{x}

R

.
Így

\begin{matrix} 0 & = I_{1} (R + R_{1}) - I_{3} R_{1} & (2'.a) \\ 0 & = + I_{2} (R_{x} + R_{2}) - I_{3} R_{2} & (2'.b) \\ E & = - I_{1} R_{1} - I_{2} R_{2} + I_{3} (R_{1} + R_{2}) . & (2'.c) \end{matrix}

(

2'

.a) és (

2'

.b)-ből

\begin{matrix} I_{1} \frac{R + R_{1}}{R_{1}} = I_{2} \frac{R_{x} + R_{2}}{R_{2}} . \end{matrix}

(3. a)

A híd egyensúlyához szükséges, hogy

I_{1} = I_{2}

. Ezt felhasználva:

\begin{matrix} \frac{R}{R_{1}} + 1 = \frac{R_{x}}{R_{2}} + 1, amiből R \cdot R_{2} = R_{x} \cdot R_{1} . \end{matrix}

(3)

Ez a Wheatstone‐híd ismert összefüggése. Ezt persze egyszerűbben is megkaphatjuk, így azonban olyan kérdésekre is választ kaphatunk, amelyek korábbi ismereteink alapján nehezen, vagy egyáltalán nem lettek volna megoldhatók.
Visszatérve a (2) egyenletekre, azok jelölése egyszerűsíthető a következőképpen:

\begin{matrix} R_{11} I_{1} - R_{12} I_{2} - R_{13} I_{3} & = E_{1} & (4.a) \\ - R_{21} I_{1} + R_{22} I_{2} - R_{23} I_{3} & = E_{2} & (4.b) \\ - R_{31} I_{1} + R_{32} I_{2} + R_{33} I_{3} & = E_{3}, & (4.c) \end{matrix}

ahol

E_{1} = E_{2} = 0

;

E_{3} = E

;

R_{11} = R + R_{1} + R_{b}

;

R_{12} = R_{b}

;

R_{13} = R_{1}

stb.
Ezzel áttekinthető kifejezést kaptunk, amelyben

R_{i i}

i

-edik áramkörben levő eredő ellenállás,

R_{i k}

pedig az

i

-edik ág közös ellenállása (

R_{i k} = R_{k i}

). Ez a felírásmód mindig előnyösen alkalmazható.
Befejezésül egy numerikus példán számítsuk ki, mekkora ellenállás van a generátor sarkaira kötve, ha

E = 1

R = R_{x} = 10 Ω

R_{1} = 6 Ω

R_{2} = 4 Ω

R_{b} = 4 Ω

r_{b} \approx 0

. A híd ebben az állásban természetesen nincs kiegyensúlyozva.

\begin{matrix} 20 I_{1} - 4 I_{2} - 6 I_{3} = 0, \\ - 4 I_{1} + 18 I_{2} - 4 I_{3} = 0, \\ - 6 I_{1} - 4 I_{2} + 10 I_{3} = 1. \end{matrix}

Ebből tehát kiszámítható

R = E / I_{3}

.
A számításnak csak az eredményét közöljük:

\begin{matrix} I_{3} = 43 / 285 A, R \approx 6, 6 Ω . \end{matrix}