Kezdőlap


Cím:	1960. évi Eötvös Loránd fizikaverseny
Füzet:	1961/február, 87 - 93. oldal	PDF \| MathML
Témakör(ök):	Eötvös Loránd (korábban Károly Irén)

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Az Eötvös Loránd Fizikai Társulat által az 1960-ban érettségizettek számára rendezett verseny november 19-én folyt le Budapesten és 6 vidéki városban. A versenyzők 5 óráig dolgozhattak és bármilyen segédeszközt használhattak. A kitűzött feladatok a következők voltak:

M = 40 kg

tömegű, igen hosszú kocsi vízszintesen elhelyezett sínen súrlódás nélkül gurulhat. Az álló kocsi vízszintes tetejére, ezzel egy magasságban, a sínnel párhuzamosan repülve

v_{0} = 25 m/sec

sebességgel

m = 10 kg

tömegű lövedék érkezik, amely csúszva halad tovább a kocsin, miközben azt súrlódása folytán mozgásba hozza. A súrlódási együttható a lövedék és a kocsi között

μ = 0, 255

. Mi történik? Mi történik, ha a kocsi csak

80 m

hosszú? Mi történik, ha a kocsi is súrlódik a sínen

μ_{2} = 0, 0425

súrlódási együtthatóval? A súrlódási együtthatók függetlenek a sebességtől.

(Wiedemann László)

Megoldás: Számítsuk a távolságokat és az időt attól a helytől és pillanattól, amikor a lövedék elérte a kocsit. A lövedék gyorsulása, sebessége, útja legyen

a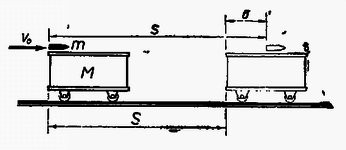

v

s

, a kocsié

A

V

S

1. ábra

A lövedék és a kocsi teteje között

μ m g

súrlódási erő működik, ez az

m

tömegű lövedéket

a = μ g

(negatív) gyorsulással lassítja, a kocsit

A = \frac{μ m g}{M} = μ g = \frac{m}{M}

gyorsulással gyorsítja. Mivel a gyorsulások állandóak, a lövedék is, a kocsi is egyenletesen változó mozgást végeznek. Ennek alapján a lövedék mozgástörvényei:

\begin{matrix} v = v_{0} - μ g t, & (1) \\ s = v_{0} t - 0, 5 μ g t^{2}, & (2) \end{matrix}

a kocsi mozgástörvényei:

\begin{matrix} V = μ g \frac{m}{M} t, & (3) \\ S = \frac{1}{2} μ g \frac{m}{M} t^{2} . & (4) \end{matrix}

A lövedék által a kocsi tetején megtett út:

\begin{matrix} σ = s - S = v_{0} t - \frac{1}{2} μ g \frac{m + M}{M} t^{2}, \end{matrix}

(5)

A lövedék csúszása a kocsi tetején akkor szűnik meg, amikor a sínhez viszonyított sebességek egyenlővé lesznek. Ezután nincs súrlódási erő a lövedék és a kocsi között, így mindketten együtt mozognak tovább egyenletes mozgással. Ennek feltétele az (1) és (3) alatti sebességek egyenlősége:

\begin{matrix} v_{0} - μ g t_{x} = μ g \frac{m}{M} l_{x} . \end{matrix}

Itt

t_{x}

a lövedéknek a kocsi tetején való megtapadásáig eltelt időt jelenti. Megoldva ezt az egyenletet:

\begin{matrix} t_{x} = \frac{v_{0}}{μ g} \cdot \frac{M}{m + M} . \end{matrix}

(6)

Ezt az időt (1)-be vagy (3)-ba helyettesítve kapjuk a közös végsebességet:

\begin{matrix} v_{x} = V_{x} = v_{0} \cdot \frac{m}{m + M} . \end{matrix}

v_{x}

közös sebességet az impulzus törvénnyel, a rugalmatlan ütközés törvényével is megkaphatjuk. Hiszen a lövedék és a kocsi közös, együttes továbbmozgása azt jelenti, hogy rugalmatlan ütközés történt. Feladatunk tulajdonképpen annak egy lehetőségét elemzi, miképpen folyhat le egy rugalmatlan ütközés a testek találkozásától közös továbbhaladásukig. A

v_{x}

közös sebesség független a súrlódási együtthatótól, attól is, vajon a súrlódási együttható tényleg független-e a sebességtől.
A lövedéknek és a kocsinak a sebesség kiegyenlítődésig megtett

s_{x}

és

S_{x}

útjait úgy kapjuk meg, hogy (2)-be és (4)-be helyettesítjük a

t_{x}

-re kapott (6) alatti eredményt:

\begin{matrix} s_{x} = \frac{v_{0}^{2}}{2 μ g} \cdot \frac{M (2 m + M)}{{(m + M)}^{2}}, \\ S_{x} = \frac{v_{0}^{2}}{2 μ g} \cdot \frac{M m}{{(m + M)}^{2}} . \end{matrix}

A lövedéknek a kocsi tetején megtett teljes csúszási hossza:

\begin{matrix} σ_{x} = s_{x} - S_{x} = \frac{v_{0}^{2}}{2 μ g} \cdot \frac{M}{m + M} . \end{matrix}

A feladatban közölt számértékek mellett

a = 250 cm/{sec}^{2}

A = 62, 5 cm/{sec}^{2}

t_{x} = 8 sec

v_{x} = V_{x} = 500 cm/sec

s_{x} = 120 m

S_{x} = 20 m

σ_{x} = 100 m

. Első grafikonunk a sebességek időtől való függését tünteti fel. A pontozott vonal azt mutatja, miképpen csökkent volna nullára a lövedék sebessége, ha álló kocsi tetején futott volna végig. (Ekkor a lövedék

\frac{v_{0}}{μ g} = 10 sec

alatt állt volna meg

s_{0} = \frac{v_{0}^{2}}{2 μ g} = 125 m

hosszú hosszú úton.)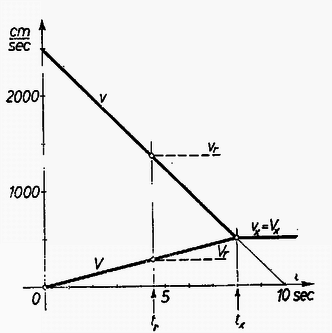

2. ábra

Érdemes megvizsgálni az energia kérdését. A lövedék

0, 5 m v_{0}^{2}

mozgási energiával érkezett

(3, 125 \cdot 10^{10} erg)

. Az együttes továbbhaladáskor a mozgási energia

0, 5 (m + M) v_{x}^{2}

(0, 625 \cdot 10^{10} erg)

. A súrlódási erő által végzett munka

μ g σ_{x} (2, 5 \cdot 10^{10} erg)

; ez hővé alakul. Behelyettesítve eredményeinket, számításunk jó próbája, hogy a kezdeti mozgási energia egyenlő a súrlódási munkavégzés és a végső mozgási energia összegével.
Mi történik akkor, ha a kocsi csak

L = 80 m

hosszú? Mivel a lövedék megállásához a mozgó kocsi tetején mért

σ_{x} = 100 m

távolság volna szükséges, ezért ebben az esetben még a sebességek kiegyenlítődése előtt elhagyja a lövedék a kocsi tetejét, azután mindketten állandó sebességgel mozognak tovább. Az elhagyás pillanatát az jellemzi, hogy ekkor

σ = L

. (5) alapján:

\begin{matrix} v_{0} t_{r} - \frac{1}{2} μ g \cdot \frac{m + M}{M} \cdot t_{r}^{2} = L . \end{matrix}

Itt

t_{r}

a kocsi tetején való tartózkodás ideje. Egyenletünk fizikai értelemmel bíró megoldása:

\begin{matrix} t_{r} = t_{x} [1 - \sqrt[]{1 - \frac{L}{s_{0}} \cdot \frac{m + M}{M}}] . \end{matrix}

s_{0}

mint rövidítő jelölés a lövedéknek álló kocsi esetében észlelt futási távolságát jelenti;

t_{x}

értékét (6) adja. A lövedék lerepülésekor tapasztalható

v_{r}

, és

V_{r}

sebességeket (7)-nek (1)-be és (3)-ba való helyettesítése, az addig megtett

s_{r}

, és

S_{r}

utakat a (2)-be és (4)-be való helyettesítése adja. Első grafikonunkon a lövedék lerepülésekor érvényes sebességeket a szaggatott vonalak tüntetik fel. Számértékeink:

t_{r} = 4, 42 sec

v_{r} = 1395 cm/sec

V_{r} = 276 cm/sec

s_{r} = 86, 12 m

S_{r} = 6, 12 m

.
Mindezek a kérdések újra feltehetők akkor, ha a kocsi és a sín között is van súrlódás

μ_{2}

a súrlódási együtthatóval. A lövedék és a kocsi között most is

μ m g

súrlódási erő működik, ezért a lövedék most is az (1) és (2) törvények által kifejezett módon mozog. Más a helyzet a kocsit illetőleg. A kocsit

μ m g

erő gyorsítja, de a sín mentén

μ_{2} (m + M) g

erő lassítja. Ugyanis a lövedék súlya szintén odanyomja a kocsit a sínhez. Ha a lövedék nem nehezedne rá a kocsira, akkor nem volna súrlódási erő a lövedék és a kocsi között, és a feladat tárgytalan volna. A kocsit végeredményben

μ m g - μ_{2} (m + M) g = (μ - μ_{2}) m g - μ_{2} M g

erő gyorsítja. Ezt

M

-mel osztva kapjuk a kocsi gyorsulását:

\begin{matrix} A = (μ - μ_{2}) g \frac{m}{M} - μ_{2} g = μ g \cdot \frac{m}{M} \cdot [1 - \frac{μ_{2}}{μ} - \frac{μ_{2}}{μ} \cdot \frac{M}{m}] . \end{matrix}

(8)

A továbbiakban ugyanúgy folytatódik a számítás, mint előbb, csak a kocsi gyorsulása számára ezt a (8) alatti értéket kell használni. A lövedéknek a kocsihoz történő megtapadásának ideje most:

\begin{matrix} t_{x} = \frac{v_{0}}{(μ - μ_{2}) g} \cdot \frac{M}{m + M} . \end{matrix}

és a közös végsebesség

\begin{matrix} v_{x} = V_{x} = v_{0} \cdot \frac{m - \frac{μ_{2}}{μ - μ_{2}} \cdot M}{m + M} . \end{matrix}

A lövedék megtapadása után

m + M

tömeg

μ_{2} (m + M) g

fékező gyorsulással mozog tovább.
Számadatainkat felhasználva

A = 10, 417 cm/{sec}^{2}

t_{x} = 9, 6 sec

v_{x} = V_{x} = 100 cm/sec

s_{x} = 124, 8 m

S_{x} = 4, 8 m

σ_{x} = 120 m

. A megtapadás után

41, 65 cm/{sec}^{2}

negatív gyorsulással

2, 4 sec

alatt

1, 2 m

-es úton áll meg a kocsi, tetején a lövedékkel. Második grafikonunk szintén a sebességek alakulását tünteti fel.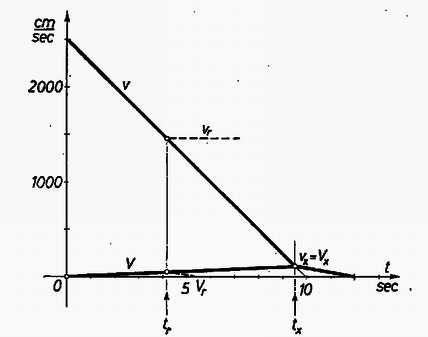

3. ábra

Ha a kocsi

L = 80 m

hosszú, akkor most is

σ = L

egyenlet adja a lerepülés

t_{r}

idejét és többi adatát. Feladatunkban

t_{r} = 4, 06 sec

v_{r} = 1485 cm/sec

V_{r} = 42 cm/sec

s_{r} = 80, 86 m

S_{r} = 0, 86 m

. Grafikonunk az ehhez tartozó sebességeket szaggatott vonalakkal ábrázolja. A lövedéktől megszabadult kocsi súrlódása folytán

1, 01 sec

alatt áll meg

0, 21 m

-en.

2. A rajz szerinti kapcsolásban a föld és

B

pont közé hosszabb idő óta

200 volt

egyenfeszültség van kapcsolva.

R

ellenállások értéke mindenütt

1 M Ω

C

kondenzátor kapacitása

1 μ F

K

pontban a vezetéket hirtelen megszakítjuk. Kérdés: mennyivel ugrik

A

pont feszültsége közvetlenül a megszakítás után (például néhány ezredmásodpercen belül)?

(Károlyházi Frigyes)

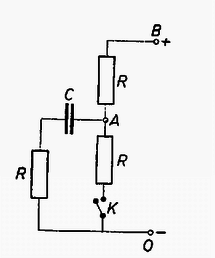4. ábra

Megoldás: Amíg az áram változatlanul folyik,

A

pont feszültsége

100 volt

és

D

-ben természetesen

0 volt

(

D

pont az ábrán a baloldali

R

ellenállás és a

C

kondenzátor között van!).

K

kapcsoló megszakítása után bizonyos (másodperces nagyságrendű) idő után

A

pont

200 volt

-os,

D

ugyancsak

0 volt

-os lesz. Közvetlenül a megszakítás után az akkor még csak

100 volt

-ra feltöltött kondenzátorba újabb töltésnek kell beáramolnia. Ezt az áramot

200 - 100 volt

indítja, de ennek az áramnak az útjába

1 + 1 = 2 M Ω

ellenállás van kapcsolva. Ha ugyanis

A

-nál beáramlik a töltés a kondenzátorba, akkor a megosztás következtében továbbküldött töltésnek

D

-nél ki kell áramolnia. A

2 M Ω

összes ellenállásra összesen

100 volt

jut, ezért mindegyik

1 M Ω

-os ellenálláson az átmenő áram 50‐50 volt-os feszültségeséssel jár együtt. Tehát közvetlenül a bekapcsolás pillanatában

A

pont feszültsége

100 volt

-ról

150 volt

-ra ugrik fel, azután aránylag lassan (másodpercnyi idő alatt) emelkedik fel

200 volt

-ra. Ezt tünteti fel grafikonunk is.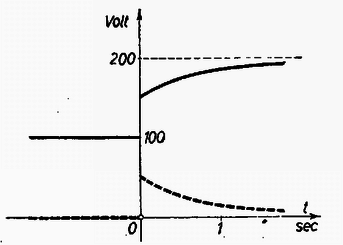

5. ábra

D

pont feszültsége a kikapcsolás pillanatában

50 volt

-ra ugrik fel, azután süllyed

0

-ra. A kondenzátor feszültsége a kikapcsolás pillanatában

100 volt

. Mivel a kondenzátor szimmetrikus kapcsolásban foglal helyet

O D

és

A B

ellenállások között, ezért érthető, a

200 volt

-os feszültség esésben úgy helyezkedik el, hogy alatta is, fölötte is

50 volt

legyen. Az ellenállásokra jutó feszültségesések igen rövid idő alatt állnak be, mert a vezetékek kapacitása igen csekély. A kondenzátor feszültségének

100 volt

-ra való emelésére

10^{- 6} \cdot 100 = 10^{- 4}

coulomb beáramlása szükséges. A

2 M Ω

-os ellenálláson

100 volt

hatására

100 : 2 \cdot 10^{- 6} = 5 \cdot 10^{- 5}

amperes áram folyik, amely (állandó erősség esetében)

10^{- 4} : 5 \cdot 10^{- 5} = 2

másodperc alatt töltené fel a kondenzátort. Ezért különül el élesen a kikapcsolással járó feszültség ugrás a későbbi lassú feltöltődéstől.

3. A sima Csendes-Óceán fölött

20 km

magasságban repülőgép repül. A Hold éppen függőlegesen felette van. Mekkorának látja a pilóta a tengerben tükröződő Holdat a tényleges Hold látszólagos nagyságához viszonyítva? A Föld rádiusza

6370 km

, a Hold távolsága a Föld középpontjától

380 000 km

(Vermes Miklós)

Megoldás: A tenger vízszintje domború gömbtükör, melynek rádiusza

R = 6370 km

. Az

S

pontban levő megfigyelő

n R

távolságban, a Hold

N R

távolságban van a Föld középpontjától. A gömbtükör a

T

méretű Holdról

K

méretű virtuális képet ad.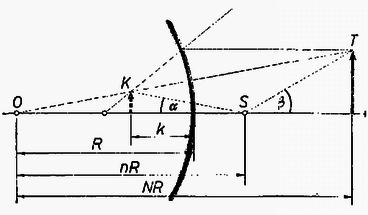

6. ábra

A feladatban adott kérdésre a látószögek aránya adja meg a feleletet. A Hold látószöge

\begin{matrix} β \approx tg β = \frac{T}{(N - n) R}, \end{matrix}

képének látószöge

\begin{matrix} a \approx tg α = \frac{K}{k + (n - 1) R} . \end{matrix}

A látószögek aránya

\begin{matrix} \frac{α}{β} = \frac{K}{T} \cdot \frac{N - n}{n - 1 + \frac{k}{R}} . \end{matrix}

(1)

A domború gömbtükör törvénye szerint

\begin{matrix} \frac{1}{k} + \frac{1}{(N - 1) R} = - \frac{2}{R} . \end{matrix}

Innen (abszolút értékben)

\begin{matrix} \frac{R}{k} = 2 + \frac{1}{N - 1} = \frac{2 N - 1}{N - 1} \end{matrix}

és

\begin{matrix} \frac{k}{R} = \frac{N - 1}{2 N - 1} . \end{matrix}

(2)

K : T

lineáris nagyítás az

O

pontban találkozó,

K

és

T

függőleges befogókkal rendelkező hasonló derékszögű háromszögek alapján, (2) segítségével:

\begin{matrix} \frac{K}{T} = \frac{R - k}{N R} = \frac{1 - \frac{k}{R}}{N} = \frac{1 - \frac{N - 1}{2 N - 1}}{N} = \frac{1}{2 N - 1} . \end{matrix}

(3)

A feladat kérdésére megkapjuk a választ, ha (1)-be helyettesítjük (2) és (3) eredményét:

\begin{matrix} \frac{α}{β} = \frac{1}{2 N - 1} \cdot \frac{N - n}{n - 1 + \frac{N - 1}{2 N - 1}} = \frac{2 N - 1}{2 N - 1} \cdot \frac{N - n}{(n - 1) \cdot (2 N - 1) + N - 1} \cdot \frac{α}{β} = \frac{N - n}{2 N n - N - n} . \end{matrix}

Néhány számszerű adat. Ha a megfigyelés

20 km

magasságban történik, akkor

n = 1, 003

Ha a Holdat nézzük,

N = 60, 6

és

α : β = 0, 9939

ha a Napot nézzük,

N = 23540

és

α : β = 0, 9940

20 km

magasságból

600 km

magasan keringő szputnyikot nézünk, akkor

n = 1, 094

és

α : β = 0, 933

A verseny eredménye: Az Eötvös Loránd Fizikai Társulat az I. díjat nem adta ki. II. díjat nyert Elsner Gábor (a budapesti Petőfi Gimnáziumban Szondy Lajos tanítványa), III. díjat nyert Mezei Ferenc (a budapesti Rákóczi Gimnáziumban Kozma Péter tanítványa). Dicséretet nyertek jutalommal Grad János (a budapesti Kölcsey Gimnáziumban Urbán János tanítványa) és Hild Erzsébet (a békéscsabai Rózsa Ferenc Gimnáziumban Molnár László tanítványa).