|
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.
Súlypont, első- és másodrendű nyomatékok
II. rész: Másodrendű nyomatékok
Térjünk vissza a tetszőleges , , derékszögű koordináta-rendszerben elhelyezett tömegpontra.
A 12. ábrának megfelelően az -edik pont koordinátái legyenek , , , az , , ill. tengelyektől való távolságai pedig , ill. , a koordináta-rendszer kezdőpontjától való távolsága . (Az , számok, mint koordináták előjeles mennyiségek, az -ek távolságokat és így pozitív számokat jelentenek.) Ezek között közismerten a következő összefüggések állanak fenn:
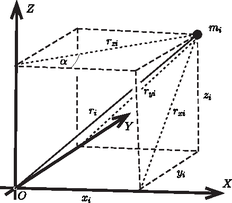 12. ábra 12. ábra
Ezekből egyszerűen következik, hogy: | | (9) |
illetve: | | (10) |
A tömegpontok koordinátái és tömegei által meghatározott következő mennyiségeket: | | (11) |
az , ill. síkokra vonatkozó másodrendű, vagy tehetetlenségi nyomatékoknak nevezzük. Most láthatjuk az elnevezések eredetét: az összegezésnél az elsőrendű nyomatékoknál a koordináták elsőfokon, a másodrendű nyomatékoknál a koordináták másodfokon szerepelnek.
Ha most pl. az síkra vonatkozó másodrendű nyomatékot alakban írjuk fel, vagyis másodrendű nyomatékra a (12) egyenlettel definiáljuk az -et, az I., II. és III. tételek változatlanul érvényben maradnak.
I. Valamely tetszőleges síkra vonatkozó nyomatékot úgy kaphatunk meg, hogy a súlyponton keresztülmenő, az eredeti síkkal párhuzamos síkra vonatkozó nyomatékhoz hozzáadjuk a súlypontba képzelt egyetlen tömegű pont nyomatékát.
II. értéke nem változik, ha mindegyik tömegpont tömegét ugyanolyan arányban növeljük vagy csökkentjük, vagy ha mindegyik tömegpont koordinátáit ugyanolyan arányban növeljük vagy csökkentjük.
III. és az síkra vonatkozó nyomaték értéke nem változik, ha az és koordinátákat tetszőlegesen megváltoztatjuk: (12) egyenletből az -et kifejezve: | | (13) |
ebből a II. és III. tétel érvényessége nyilvánvaló. Az I. tétel érvényességét úgy igazolhatjuk, hogy felírjuk a másodrendű nyomatékokat az súlysíkra (l. 2. ábra). | |
Mivel (2) szerint Ezért: és teljesen hasonló módon következik, hogy
Ezt a tételt Steiner-tételnek szokták nevezni. Ezzel a másodrendű nyomatékokra is igazoltuk az I. tétel érvényességét. Az is látható, hogy egymással párhuzamos síkok közül a súlysíkra vonatkozó nyomaték a legkisebb. A | | (15) |
mennyiségeket az , , ill. tengelyekre, a mennyiséget pedig a kezdőpontra vonatkozó másodrendű vagy tehetetlenségi nyomatéknak nevezzük. A (7)‐(10) összefüggéseknek megfelelően a különböző másodrendű nyomatékok között a
és összefüggések állanak fenn.
Az I ‐ III. tételek a definíciókból következtethető kis módosításokkal a tengelyekre és pontokra vonatkozó tehetetlenségi nyomatékokra is érvényesek. Tengelyre vonatkozó tehetetlenségi nyomatékoknál e tételek:
I. Tengelyre vonatkozó másodrendű nyomatéknál (14) és (17)-ből következik, hogy valamely tengelyre vonatkozó másodrendű nyomatékot a tengellyel párhuzamos súlyegyenesre vonatkozó másodrendű nyomaték és a súlypontba képzelt egész tömeg másodrendű nyomatékából tehetjük össze.
II. Például az tengelyre vonatkozó másodrendű nyomatékot alakban írhatjuk fel, ahol most -nek választjuk a pontrendszernek valamilyen, az tengelyre vonatkozó, nullától különböző tetszőleges radiális méretét. (Pl. valamely tömegpontnak az tengelytől való távolságát, vagy két tömegpont ezen távolságainak különbségét stb.) A (21) egyenlet által így definiálható megint változatlan marad a tömegpontok tömegeinek vagy koordinátáinak ugyanolyan állandóval való megszorzásakor.
III. és így értéke most csak az egyes tömegpontoknak az tengelytől való távolságától függ. Ezért pl. az tengely körüli sugarú henger palástjain levő összes tömegpontok tömege a palást egyetlen tetszőleges pontjában gyűjthető össze.
Pontra vonatkozó tehetetlenségi nyomatéknál e tételek:
I. Pontra vonatkozó másodrendű nyomatéknál (14) és (18)-ból következik, hogy tetszőleges pontra a másodrendű nyomaték a súlypontra vonatkozó másodrendű nyomaték és a súlypontba képzelt egész tömeg másodrendű nyomatékának összege.
II. A pontra vonatkozó másodrendű nyomatékot alakban írhatjuk fel, ahol a pontrendszernek valamilyen, a kezdőpontra vonatkozó nullától különböző tetszőleges radiális mérete (pl. valamelyik tömegpontnak a kezdőponttól való távolsága, két tömegpont ilyen távolságának különbsége stb.), az előző transzformációkra nézve most is állandó.
III. és értéke csak a tömegpontoknak az alapponttól való távolságától függ. Ezért pl. a kezdőpont körüli sugarú gömb felületén levő összes tömegpontok a felület tetszőleges pontjába gyűjthetők össze.
(17)‐(20)-ból következik, hogy ha pl. az összes tömegpontok az tengelyen feküsznek (vonaldarabokra):
Ha az összes tömegpontok az síkban feküsznek (síkidomokra):
Megint bemutatjuk néhány példán, hogy az I-III. tételek segítségével hogyan számíthatunk tehetetlenségi nyomatékot integrálás nélkül.
6. példa. Egyenletes tömegeloszlású, hosszúságú vonaldarab másodrendű nyomatéka a súlypontjára.
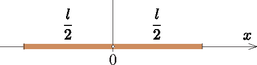 13. ábra 13. ábra
Bontsuk a vonalat két féldarabra (13. ábra), és alkalmazzuk az I. és II. tételt: | |
ebből: Tehát (24) szerint a súlyponton keresztülmenő merőleges tengelyre Számítsuk még ki a tehetetlenségi nyomatékot a vonaldarab végpontjára is. A vonaldarab végpontjára a Steiner-tétel szerint:
7. példa. Lineárisan növekvő sűrűségű, hosszúságú egyenes vonaldarab tehetetlenségi nyomatéka a súlypontjára.
Bontsuk a vonalat két féldarabra, akkor a 2. példa meggondolásai szerint a jobb oldali vonaldarab összetehető egy állandó sűrűségű, tömegű és egy a jobb oldali vonaldarabbal azonos, lineárisan növekvő sűrűségű, tömegű vonalból. 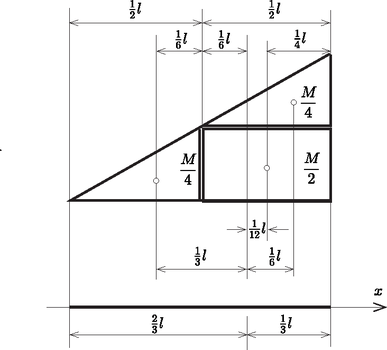 14. ábra 14. ábra
Mivel a súlypontok távolságai -tól rendre (l. a 2. példát és a 14. ábrát) , és , az I. és II. tétel és az előző példa alapján megint felírhatjuk, hogy:
innen: a súlyponton keresztülmenő merőleges tengelyre: A bal oldali végpontra most | |
8. példa. Négyzetesen növekvő sűrűségű, hosszúságú egyenes vonaldarab tehetetlenségi nyomatéka a súlypontjára. Bontsuk a vonalat két féldarabra, akkor az 5. példa szerint a vonaldarab jobb oldala három részre bontható, egy a bal oldallal megegyező, egy lineárisan növekvő sűrűségű és egy állandó sűrűségű vonalra. Tömegek és súlyponttávolságaik az 5. példából ismeretesek, illetve kiszámíthatók (15. ábra). 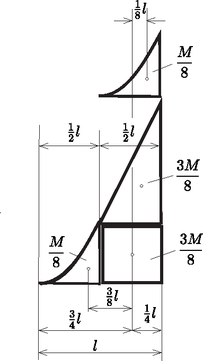 15. ábra 15. ábra
Így felírható, hogy:
Ebből: és így a súlyponton keresztülmenő tengelyre: A bal oldali végponton pedig:
9. példa. Körlap tehetetlenségi nyomatékai (lásd a 16. ábra szerinti elrendezést).
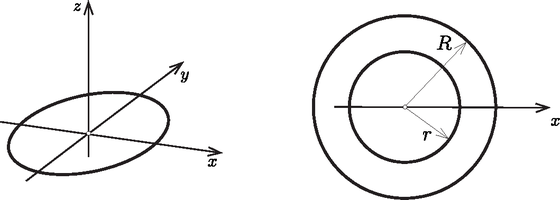 16. ábra 16. ábra
számításánál az sugarú kör kerületén fekvő tömegpontokat az tengelyen összegyűjtve, a kör lineárisan növekvő sűrűségű hosszúságú vonallal helyettesíthető. e vonalnak a kezdőpontjára vonatkozó tehetetlenségi nyomatékával egyezik meg, vagyis a 7. példa szerint (27) szerint, mivel most szimmetria okokból nyilván ,
10. példa. Gömb tehetetlenségi nyomatékai a súlypontjában elhelyezett koordináta-rendszerben. A számításnál most az sugarú gömb felületén fekvő tömegpontok gyűjthetők össze egy tengelyen, a gömb négyzetesen növekedő sűrűségű hosszúságú rúddal helyettesíthető. a rúdnak kezdőpontjára vonatkozó tehetetlenségi nyomatékával egyezik meg, vagyis a 8. példa szerint: (20) szerint, mivel most a szimmetria miatt
11. példa. Egyenes körhenger tehetetlenségi nyomatékai a 17. ábra szerint a súlypontjában elhelyezett koordináta-rendszerben. 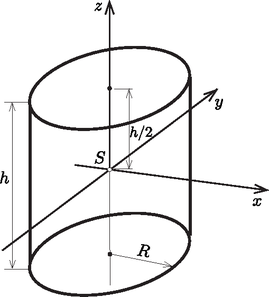 17. ábra 17. ábra
számításánál a hengert az síkba összenyomva egyenletes sűrűségű körlapot kapunk. Így a 9. példa alapján számításánál a hengert a tengelybe nyomva össze egyenletes sűrűségű, hosszúságú vonaldarabot kapunk. Erre a 6. példa szerint Ezekből a szimmetria miatt, a (17‐20) összefüggések felhasználásával:
Természetesen ez az nem azonos az elsőrendű nyomaték -ével.Félreértések elkerülése végett megjegyezzük, hogy általánosan rendű nyomatékra ez a tétel már nem érvényes. |
 PDF | MathML
PDF | MathML