A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.Súlypont, első- és másodrendű nyomatékok I. rész
Legyen adva a térben tetszőleges elrendezésben egy tömegpontból álló rendszer. A tömegpontok tömegei legyenek . Legyen továbbá a tömegpont rendszer egész tömege. Vegyünk fel tetszőlegesen egy térbeli derékszögű , , koordináta-rendszert. Az pont koordinátáit jelöljük , , ill. -vel (1. ábra). 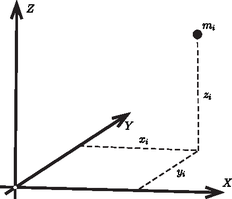 1. ábra 1. ábra A tömegpontok tömegei és koordinátái által meghatározott következő mennyiségeket, | | (1) |
az , , ill. síkokra vonatkozó elsőrendű nyomatékoknak nevezzük. Ezekre vonatkozólag fennáll a következő érdekes tétel:
Létezik a térben egy és csak is egy olyan pont, amelyben mint kezdőpontban elhelyezett tetszőleges irányítású derékszögű koordináta-rendszerben a három elsőrendű nyomaték mindegyike nulla.
Bebizonyítjuk, hogy ezen pont az | | (2) |
koordinátájú pont.
Vegyünk fel az pontban egy az , , koordináta-rendszerrel párhuzamos tengelyű , , koordináta-rendszert (2. ábra).
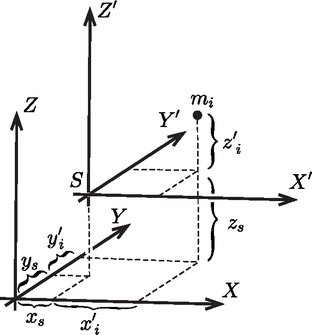 2. ábra 2. ábra
Ekkor | | (3) |
lévén az új koordináta-rendszer síkjaira az elsőrendű nyomatékok nullák. Pl. síkra (3) miatt: | |
Tekintetbe véve (1)-et és (2)-t Teljesen hasonlóan bizonyítható a másik két koordinátasíkra vonatkozó elsőrendű nyomatékok eltűnése is.
Ha új koordináta-rendszerünket valamelyik koordináta tengely körül elforgatjuk, az elsőrendű nyomatékok értéke változatlanul nulla marad. Igazoljuk pl. azt az esetet, mikor a tengely körül szöggel forgatunk. -re állításunk nyilvánvaló. ill. -re pedig a következőképpen látható be: Fejezzük ki ill. -t a tömegpontoknak a tengelytől való távolságaival és ezeknek a tengellyel bezárt szögeivel (3. ábra).
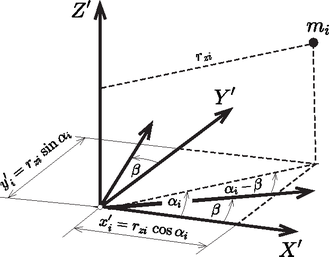 3. ábra 3. ábra
A szöggel való elforgatás után ezen kifejezésekben csak az szögek változnak meg, mégpedig mindegyik -val csökken. Így az új nyomatékok
illetve | |
lesznek.
Ugyanezen igazolás alkalmazható az és tengelyek körüli elforgatásra is. Mivel három egymásra merőleges tengely körüli forgatással a koordináta-rendszer bármely térbeli elforgatása létrehozható, igazoltuk, hogy az | |
A (2) egyenletekből az is látható, hogy az S pontbeli tetszőleges X'Y'Z' koordináta-rendszert eltolva az xs, ys ill. zs közül legalább az egyik már nem nulla, és így a három elsőrendű nyomaték közül legalább egy már nem marad nulla. Tehát S-en kívül más fenti tulajdonságú pont nincsen.
Az S pontot a rendszer tömegközéppontjának, vagy súlypontjának nevezzük. Az utóbbi elnevezés onnan származik, hogy a tömegpontok egymáshoz viszonyított helyzetének megtartása, vagyis a rendszer ,,megmerevítése'' esetén a tömegpontok súlyerőinek eredője, a térben tetszőlegesen végzett elforgatás után, a pontoknak minden helyzetében a súlyponton keresztülmenő függőleges egyenesbe esik. A következőképpen láthatjuk be, hogy ez valóban így van. Legyen a 2. ábra szerinti elrendezésnél az X'Y' sík vízszintes, és határozzuk meg a gmi függőleges (Z tengely irányú) súlyerők eredőjének a helyzetét. Pl. az Y' tengelyre felírhatjuk, hogy a súlyerők forgatónyomatékának összege szükségképpen megegyezik az eredő forgatónyomatékával. Mivel a gmi súlyerőnek az Y' tengelyre a karja xi a forgatónyomaték ∑i=1ngmix'i=gN'yz=0 lévén, az eredőnek az Y' tengelyre vonatkozó karja nulla, vagyis az eredőnek az Y'Z' síkban kell lennie. Az X' tengelyre hasonlóképpen kiszámított forgatónyomaték is nulla, vagyis az eredő a Z'X' síkban is benne fekszik. Ezért az eredő rajta fekszik e két sík metszésvonalán, a Z' tengelyen, vagyis a súlypontokon keresztülmenő merőlegesen.
A súlyponton keresztülmenő síkot súlysíknak, a súlyponton keresztülmenő egyenest súlyvonalnak hívjuk.
Az elsőrendű nyomatékok (és így M-mel osztva a súlysíkok) helyzetei az (1) egyenletek segítségével elvileg mindig meghatározhatók, gyakorlatilag azonban a térben folytonos tömegelosztás esetén az (1) egyenletekben szereplő összegezés végtelen sok tagból álló összeggé, ,,integrállá'' alakul át. Ennek zárt alakbeli kiszámítása még az integrálszámítás ismertében sem lehetséges minden esetben. Aki pedig nem járatos az integrálszámításban, az egyszerűbb esetekben sem boldogul. Néha segítséget nyújt az, hogy ha a tömegpontok rendszerének (ill. a testnek) szimmetriasíkja, tengelye vagy pontja van, akkor az súlysík, súlyvonal ill. súlypont. Ez nyilvánvaló, mert a szimmetriasíkra, ill. a szimmetriatengelyen vagy ponton keresztül fektetett síkra vonatkozólag az (1) összegezésben ugyanazon tagok párosával különböző előjellel lépnek fel, és így az elsőrendű nyomaték nulla lesz. Ebből az is következik, hogy ha a tömegpontok mind egy síkba esnek, akkor a súlypont is ebben a síkban fekszik. Ezek általában közismert tények. A következőkben három olyan tételt fogunk ismertetni, melyeknek segítségével a nyomatékok meghatározása a legtöbb gyakorlatilag előforduló esetben folytonos tömegeloszlás esetén is integrál számítás nélkül sikerül.
A (2) egyenletekből fejezzük ki a nyomatékokat: | Nyz=MXs;Nzx=MYs;Nxy=MZs. | (4) |
Ezen egyenleteket a következőképpen fogalmazzuk meg:
I. Valamely tetszőleges síkra vonatkozó nyomatékot úgy kaphatunk meg, hogy a súlyponton keresztülmenő, az eredeti síkkal párhuzamos síkra vonatkozó nyomatékhoz (ti. itt most: nullához) hozzáadjuk a súlypontba képzelt egyetlen M tömegű pont nyomatékát.
Ez a kissé bonyolultnak látszó megfogalmazás, miként később látni fogjuk, a másodrendű nyomatékokra is érvényes lesz. I.-ből következik, hogyha valamely tömegpontrendszer vagy test olyan alrendszerekre (testrészekre) bontható, melyeknek súlypontjait ismerjük, a nyomaték számításánál az alakrendszerek (testrészek) helyettesíthetők a súlypontjukba helyezett olyan tömegpontokkal, melyeknek tömege az alrendszert alkotó pontok (testrészek) egész tömegével egyenlő.
Írjuk fel pl. az YZ síkra vonatkozó elsőrendű nyomatékot a következő alakban: ebben legyen lx a tömegpontok rendszerének (testnek) valamilyen tetszőleges X irányú lineáris jellemző (nullától különböző) mérete (pl. valamelyik nem YZ síkban fekvő tömegpontnak x koordinátája, vagy két tetszőleges tömegpont x koordinátájának különbsége stb.) ax az (5) egyenlet által definiált dimenzió nélküli szám, vagyis | ax=NyzMlx=∑i=1nmixilx∑i=1nmi=xslx. | (6) |
A (6) egyenletből nyilvánvaló a következő két tétel:
II. ax értéke nem változik, ha mindegyik tömegpont tömegét ugyanolyan arányban növeljük, vagy csökkentjük, vagy ha mindegyik tömegpont koordinátáit ugyanolyan arányban növeljük vagy csökkentjük.
Más szóval: hasonló tömegpontrendszerekre (testekre) ax ugyanakkora. ax tehát független a testek nagyságától, csak a testek alakjától és a relatív tömegeloszlástól függ.
III. ax és az YZ síkra vonatkozó nyomaték értéke nem változik, ha az Yi és Zi koordinátákat tetszőlegesen megváltoztatjuk.
Ebből következik, hogy az egyes vagy az összes Yi és Zi koordináták tetszőleges számmal szorozhatók, a test Y és Z tengely irányú méretei tetszőleges arányban növelhetők vagy csökkenthetők. Az utóbbi olyan mértékű is lehet, hogy minden Yi és Zi nullává tehető, vagyis a tömegpontok mind az X tengelyre gyűjthetők össze. (Természetesen ez az eljárás csak az ax ill. Nyz értékek meghatározása szempontjából alkalmazható, ilyen átalakításnál az Nzx és Nxy értékek nem maradnak változatlanok).
A következő néhány példán bemutatjuk a törvények sokoldalú használhatóságát:
1. példa: Egyenletes tömegeloszlású (az egységnyi hosszra eső tömeg ϱ0=állandó) l hosszúságú egyenes vonaldarab súlypontja szimmetria okokból nyilvánvalóan a vonaldarab felezési pontjában van. Ugyanazt az eredményt bonyolultabban, de a későbbi példák jobb megértése kedvéért más úton is megkaphatjuk. Határozzuk meg az ismeretlennek tekintett ax segítségével.
A 4. ábrán ϱ-t x függvényeként ábrázoltuk. 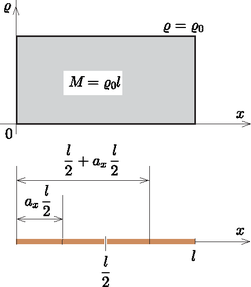 4. ábra 4. ábra
Mivel ax értéke szempontjából csak a relatív tömegeloszlás lényeges, ϱ0 értéktől nem függ, csak az a lényeges, hogy ϱ az egész vonaldarab mentén állandó. A beárnyékozott M=lϱ0 terület adja meg az egész vonaldarab tömegét.
Bontsuk szét a vonaldarabot felezőpontjával két darabra. Mindegyik fél vonaldarab ugyancsak egyenletes tömegeloszlású, csak az x koordináták csökkentek arányosan (ti. feleződtek). Ezért mindegyik fél vonaldarab bal oldali végpontjára ax megegyezik az eredetiével. Mivel mindegyik fél vonaldarab feleakkora tömegű és hosszúságú, mint az eredeti, és mivel a jobb oldali vonaldarab bal oldali végpontja a kezdőponttól l/2 távolságra van, az I. tétel alapján az (5) egyenlet segítségével a nyomatékra a következő egyenletet írhatjuk fel: Ml-lel egyszerűsítve ax-re a következő elsőfokú egyenletet kapjuk: ebből ax=12, vagyis: xs=12l.
2. példa: Határozzuk meg az l hosszúságú lineárisan növekedő sűrűségű (ϱ=kx) egyenes vonal darab súlypontját. Mivel a vonaldarabot az előző módon megfelezve, a jobb oldali fél vonaldarab egy állandó sűrűségű és egy a bal oldali vonaldarabbal megegyező tömegeloszlású vonaldarabra bontható szét. Az egész és a fél vonaldarabok tömegét megint az árnyékozott területek adják meg. Ha az egész vonaldarab tömege M=kl2/2, az 5. ábra szerint a bal oldali félé M/4, az állandó sűrűségűé pedig M/2.
5. ábra
A bal oldali vonaldarabon és az egész vonaldarabon ax most is azonos. Ez az OCD▵ és OAB▵ hasonlóságából következik, mert hiszen a III. tétel szerint ax változatlan marad az x koordinátáknak és a ϱ sűrűségnek állandóval való szorzására. Ezért az ax-re az előző példához hasonló meggondolásokkal most a következő egyenletet kapjuk: | Maxl=M4axl2+M4(l2+axl2)+M2(l2+12l2), |
itt az utolsó tag az állandó sűrűségű rúd nyomatéka.
Ebből: ax=23 és xs=2l/3.
3. példa: Egyenletes tömegeloszlású (felületegységenként állandó sűrűségű) háromszög súlypontjának meghatározása. Koordináta-rendszerünket vegyük fel a 6. ábrán látható módon.
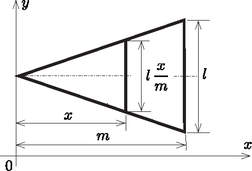 6. ábra 6. ábra
Mivel az x távolsággal a szélességi méret lineárisan nő, a háromszög azonos x koordinátáinak pontjait a III. szerint az X tengelyre gyűjtve össze, lineárisan növekvő sűrűségű vonalat kapunk, vagyis a 2. példát kapjuk. Valóban közismerten a háromszög súlypontja a csúcspontjából 2/3m távolságban az alappal párhuzamos egyenesen fekszik.
Ugyanezt az eredményt másképpen is megkaphatjuk. A II. és III. tétel szerint a súlypont távolsága azonos minden m magasságú háromszögre. (A két tétel által megengedett transzformációk segítségével bármely két ilyen háromszög egymásba transzformálható.) Határozzuk meg a legegyszerűbbre, az egyenlő oldalú háromszögre.
Mivel a súlypont a szimmetriatengelyeken fekszik, összeesik a magassági ponttal, a belül írható kör középpontjával stb. Ebből a pontból a háromszöget a 7. ábra szerinti három egybevágó háromszögre bonthatjuk, ezek területe tehát harmada az eredeti háromszögének, mivel a lenti háromszög alapja megegyezik az eredeti háromszögével, magasságának harmadakkorának kell lennie. Vagyis a súlypont a csúcsponttól számítva valóban 2/3m távolságra van.
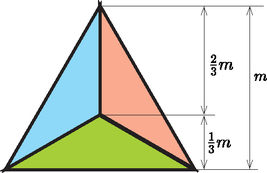 7. ábra 7. ábra
4. példa: Tetszőleges alapgörbéjű, homogén sűrűségű kúp súlypontjának távolsága az alaptól.
Mindezen kúpok közös tulajdonsága, hogy a csúcsponttól x távolságra levő alappal párhuzamos metszetük területe négyzetesen nő az x távolsággal (8. ábra).
 8. ábra 8. ábra
ax szempontjából tehát mindezen kúpok egymásba transzformálhatók. Ezért ax megegyezik a négyzetesen növekvő sűrűségű vonaldarab ax-ével, amire még visszatérünk. ax-et legegyszerűbben a szabályos tetraédernél határozhatjuk meg az egyenlő oldalú háromszöghöz hasonló módon (9. ábra).
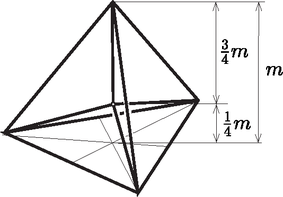 9. ábra 9. ábra
A szimmetriasíkok metszéspontjában levő súlypontot a csúcsokkal összekötve, négy egybevágó gúlát kapunk, melyek közül az alsónak alaplapja megegyezik az eredeti tetraéder alaplapjával, így a súlypontnak az alaplap felett 1/4m magasságban, a csúcsponttól 3/4m magasságban kell lennie. Vagyis ax=3/4.
5. példa: Ha ismerjük a parabola területi képletét, a 2. példában alkalmazott eljárással megkaphatjuk a négyzetesen növekvő sűrűségű egyenes vonaldarabra ugyanazt az ax=3/4-et. Mi most fordítva fogunk eljárni, ax-et az előző példából ismerve, a ϱ=kx2 parabola és az X tengely közti területet határozzuk meg (10. ábra).
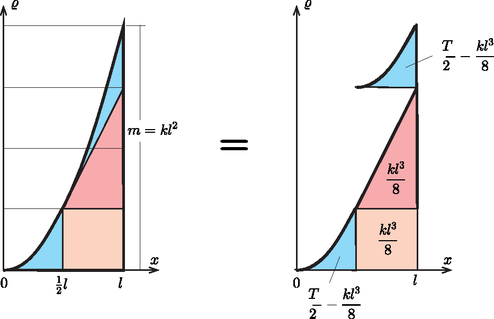 10. ábra 10. ábra
Vizsgáljuk tehát a ϱ=kx2 négyzetesen növekvő sűrűségű vonaldarabot. Mivel: | kx2=k(x-l2)2+kl(x-l2)+kl24, |
az l távolságot megfelezve, a jobb oldali rész területe egy téglalap, egy vele azonos területű háromszög és egy a bal oldali résszel megegyező parabolának a területéből tevődik össze. Azért, ha az egész rúd tömegét, vagyis a keresett területet T-vel jelöljük, a kis parabolák területe T2-kl38 lesz. Most alkalmazzuk szokásos módszerünket, tudván, hogy parabolára ax=3/4, háromszögre 2/3, téglalapra 1/2.
T34l=(T2-kl38)34l2+kl38(12l+12l2)+kl38(12l+23l2)+(T2-kl38)(12l+34l2).
Ezt T-re megoldva: a területi képlet tehát szavakkal: alap szorozva a magassággal és osztva hárommal.
 11. ábra 11. ábra
A 10. ábrabeli felosztás T ismeretében a 11. ábrán látható módon alakul.
|
 PDF | MathML
PDF | MathML 








