Cím: Az 1961. évi Arany Dániel Matematikai Versenyek I. fordulóján kitűzött feladatok megoldása:A kezdők versenye
Szerző(k):  Lukács Ottó ,  Scharnitzky Viktor 
Füzet: 1961/november, 97 - 99. oldal  PDF  |  MathML 
Témakör(ök): Arany Dániel

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Kezdők (I. osztályosok) versenye

 

1. feladat. Oldjuk meg x-re a következő egyenletet:
pq-pxqx-1=qp-qxpx-1.
p és q milyen értékeinél van gyöke az egyenletnek?
 

Megoldás. Az egyenletnek nincs értelme, ha valamelyik nevező 0; feltesszük tehát, hogy p≠0, q≠0, és nem fogadunk el olyan p, q számpárt, amelyből px-1=0, qx-1=0, vagyis px=1, qx=1 adódik. A nevezők szorzatával szorozva
p2(qx-1)(px-1)-p2qx(px-1)=q2(qx-1)(px-1)-pq2x(qx-1).
A zárójelek felbontása, rendezés és összevonás után x-re elsőfokú egyenletet kapunk:
(p3-q3)x=p2-q2.
Ha p=q, akkor ez az egyenlet ‐ és természetesen az eredeti is ‐ minden x-re teljesül, nincs határozott, egyértelmű megoldás. Ha p≠q, akkor p3-q3≠0-val osztva és p-q-val egyszerűsítve:
x=p+qp2+pq+q2.
Ezzel az egyenletet megoldottuk. Látható, hogy
px=p2+pqp2+pq+q2=1
csak q=0 mellett, qx=1 pedig csak p=0 mellett következnék be. Ezeket már kizártuk, tehát az egyenletnek mindig van határozott gyöke, ha p≠0, q≠0, és p≠q.
 

2. feladat. Szerkesszük meg az ABC háromszöget, ha ismerjük A-nál levő szögét, B-ből kiinduló súlyvonalát és C-ből kiinduló magasságvonalát. Magyarázzuk meg a szerkesztés minden lépését.
 

I. megoldás. Legyen az adott magasság mc, a súlyvonal sb, A C csúcsot az α szög AB=c szárától mc távolságra haladó d párhuzamos metszi ki a másik szárból. Az AC oldal F felezőpontjából sb sugárral rajzolt kör kimetszi az α szög c szárából a B csúcso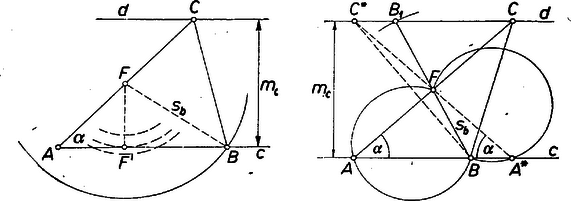t.
 
 

A feladat megoldhatóságának eleve feltétele, hogy 0<α<180∘ legyen. Így C mindig egyértelműen szerkeszthető. A feladatnak 1, 2, 1, vagy 0 megoldása van aszerint, hogy a használt körív az α szög másik szárát 1, vagy 2 pontban metszi, vagy érinti, vagy nem is érinti. Az F pont merőleges vetületét AB-n F'-vel jelölve α<90∘ mellett az említett négy eset valamelyike aszerint áll fenn, hogy
sb≧FA,FA>sb>FF',sb=FF',sb<FF'(FF'=mc/2).
Ha α≧90∘, akkor legfeljebb 1 megoldás van, sb>FA mellett.
 

II. megoldás. B-nek F-re vett B1 tükörképe a C-n át AB-vel párhuzamos d egyenesen van. Ebből adódik a következő szerkesztés.
Felveszünk két egymástól mc távolságra fekvő c és d párhuzamost és c-n a B csúcsot. A B-körüli 2sb sugarú körívvel d-ből kimetsszük B1-et. BB1-nek F felezőpontja és a B pont alkotta szakasz A-ból α szög alatt látszik, tehát az A csúcs a c egyenes és a BF fölé rajzolt α nyílású látószögkörívpár metszéspontja. Végül A tükörképe F-re C.
Ha 2sb<mc, akkor B1 nem szerkeszthető, a feladatnak nincs megoldása. Ha 2sb≧mc, akkor 2, 1, vagy 0 a megoldások száma aszerint, hogy a BF fölé rajzolt két körív mindegyike metszi c-t a B-től különböző pontban, vagy csak egyikük, vagy egyikük sem.
 

3. feladat. Bizonyítsuk be, hogy ha egy 7-tel osztható háromjegyű szám utolsó két számjegye egyenlő, akkor számjegyeinek összege is osztható 7-tel.
 

I. megoldás. A feladat teljes értékű megoldásának számít, ha a két egyenlő jegyre végződő háromjegyű számok közül kikeressük az összes 7-tel oszthatókat és mindezeken ellenőrizzük, hogy számjegyeik összege valóban osztható-e 7-tel. (Ilyen eljárást azonban csak akkor ügyes használni, ha valamilyen rendszerezéssel munkamegtakarítást tudunk elérni az egyenkénti kikereséssel szemben.)
A kérdéses számok kiválogatását könnyűvé teszi a következő észrevétel. A számokat két rész összegére bontva: a százasra és a két egyenlő jeggyel írt számra, ezeknek 7-tel való osztási maradéka vagy mindkét részben 0, vagy összegük 7. (Pl. 322=7⋅46-ban 300 és 22-nek 7-es maradéka 6, illetőleg 1.) Állítsuk tehát össze, mely két egyenlő jeggyel írt számok adnak 7-tel osztva 0, 1, 2, 3, 4, 5, 6 maradékot, másrészt, hogy mely kerek százasok adnak rendre 0, 6, 5, 4, 3, 2, 1 maradékot, ezek összeadásából megkapjuk valamennyi szóban forgó számot.
 



|MaradékVégződésMaradékSzázasA számA jegyek összege|000,770700700,77717,21|122,996300322,39917,21|244560064414,14|3664200,900266,96614,21|411,883500511,58817,21|5332100,800133,83317,14|655140045514,14   

 


Valóban valamennyi számban a számjegyek összege osztható 7-tel.
 

II. megoldás. Legyen a szóban forgó háromjegyű szám abb¯=100a+10b+b=100a+11b, így számjegyeinek összege a+2b.Tegyük fel, hogy N=100a+11b 7-nek többszöröse, be kell bizonyítanunk, hogy akkor a+2b is osztható 7-tel. Vonjuk ki N-ből a 7-tel szintén osztható 98a+7b-t, a maradék: 2a+4b=2(a+2b) szintén osztható 7-tel. Mivel 7 és 2 relatív prím számok, ez csak úgy lehetséges, ha a+2b osztható 7-tel.1
 

Megjegyzések. 1. A II. megoldás bizonyítása meg is fordítható, és így igaz a következő állítás: ha egy háromjegyű szám utolsó két jegye megegyezik, és számjegyeinek összege osztható 7-tel, akkor a szám is osztható 7-tel; ha pedig a számjegyek összege nem osztható, akkor a szám sem osztható 7-tel.
2. Az algebrai megoldás többet igazol a bizonyítandó tételnél: nemcsak háromjegyű, hanem bármely 100a+11b alakú szám ahol a és b tetszőleges egész számok ‐ akkor és csak akkor osztható 7-tel, ha a+2b osztható. Pl. 100⋅243+11⋅22=24542 szám esetén 243+2⋅22=287 osztható 7-tel, tehát a szám is osztható 7-tel. Mivel azonban általában nem könnyű egy egész számról azt megállapítani, hogy írható-e egész a, b-vel 100a+11b alakban, ahol b≧10, azért ez a tétel oszthatósági vizsgálatok könnyítésére csak két egyező jegyre végződő számoknál lehet hasznos.
1Ez pl. abból következik, hogy 4⋅2(a+2b)=7(a+2b)+(a+2b) is, és így a+2b is osztható 7-tel.