Cím: Az 1961. évi Országos Középiskolai Matematikai Tanulmányi Verseny I. fordulóján kitűzött feladatok megoldása
Szerző(k):  Lukács Ottó ,  Scharnitzky Viktor ,  Surányi János 
Füzet: 1961/október, 49 - 53. oldal  PDF  |  MathML 
Témakör(ök): OKTV

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

1. feladat. Egy léggömb középpontját két földi megfigyelő 45∘, illetőleg 22,5∘ emelkedési szögben látja. Az első megfigyelő délre, a második északnyugatra van a léggömb talppontjától, egymástól való távolságuk 1600 méter. Milyen magasan lebeg a léggömb a vízszintes talaj fölött ?

 

I. megoldás. Legyen a léggömb L, merőleges vetülete a vízszintes talajon (talppontja) T; a megfigyelők A és B; a léggömb emelkedési szöge az A pontból α=45∘, a B pontból β=22,5∘, a két megfigyelő távolsága AB=d=1600m, a TA déli és TB északnyugati irányok hajlásszöge 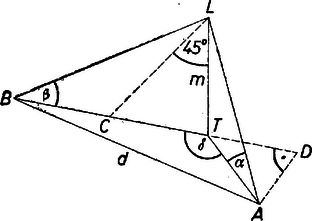δ=135∘ (1. ábra).
 
 
1. ábra
 

‐ Az ATL derékszögű háromszög egyenlő szárú, mert α=45∘, tehát AT egyenlő a keresett TL magassággal ‐ jelöljük ezt röviden m-mel. Húzzunk a BTL háromszög L csúcsából LT-vel 45∘-ot bezáró egyenest. Mivel BLT∢=90∘-LBT∢=67,5> >45∘, azért egyenesünk a BT szakaszt metszi egy C pontban. TC=TL=m és BLC∢=BLT∢-45∘=22,5∘=TBL∢=CBL∢, vagyis a BCL háromszög egyenlő szárú: BC=CL=m2.
Jelöljük az A pont merőleges vetületét a BT egyenesen D-vel. Ekkor az ADT derékszögű háromszög is egyenlő szárú, mert T-nél levő szöge ATD∢=180∘-ATB∢=45∘, s így AD=DT=m/2.
Az ABD derékszögű háromszög átfogójának hossza adott: d=1600m, befogóit pedig sikerült kifejezni a keresett m magassággal: AD=m/2, BD=BC+CT+TD=m2+m+m/2. Így Pythagorász tétele szerint
AD2+DB2=(m2)2+(m2+m+m2)2=AB2=16002.
Innen
m2(12+2+22+1+2+2+12)=m232(2+1)=16002,
vagyis
m=160032(2+1)=16002-132=80038(2-1)⋅3=800312-72≈500m
(méterre kerekítve).
 

II. megoldás. A feladatot általánosan, a talpponton átmenő vízszintes síkban tetszőleges helyzetű A és B megfigyelők és tetszőleges hegyes α és β emelkedési szögek esetére oldjuk meg.
Az ATL, BTL derékszögű háromszögből AT=mctgα, BT=mctgβ, és így az ATB háromszögből a koszinusz-tétel alapján
d2=m2ctg2α+m2ctg2β-2m2ctgαctgβcosδ==m2(ctg2α+ctg2β-2ctgαctgβcosδ),
és innen
m=dctg2α+ctg2β-2ctgαctgβcosδ.
(Ha ABT valóságos háromszög, akkor a négyzetgyök alatt álló kifejezés pozitív, mert a koszinusz-tétel érvényes.)
A d=1600m, α=45∘, β=22,5∘, δ=135∘ adatokkal m≈500m.
 

2. feladat. Bizonyítsuk be, hogy ha egy négyszög két szemben fekvő oldalának felezőpontjait összekötő szakasz egyenlő a másik két oldal számtani közepével, akkor a négyszög trapéz.
 

Megoldás. Legyen az ABCD négyszög (2. ábra) AD és BC oldalának felezőpontja E 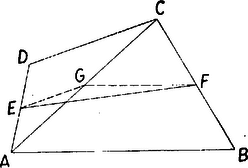és F, és EF=(AB+DC)/2.
 
 
2. ábra
 

Azt fogjuk bebizonyítani, hogy AB és CD párhuzamosak. Jelöljük az AC átló felezőpontját G-vel. Ekkor egyrészt EG, mint az ACD háromszög középvonala, párhuzamos DC-vel és fele akkora; és hasonlóan az ABC háromszög GF középvonala párhuzamos AB-vel és fele akkora. Másrészt az EFG háromszögből ‐ ha ez valódi háromszög, tehát G nem esik az EF egyenesre ‐
EF<EG+GF=12(DC+AB).
Eszerint a bal oldal a jobbal egyenlő csak akkor lehet, ha G az EF egyenesen van. Ekkor
DC||EF||AB,
vagyis az ABCD négyszög trapéz, és ezt kellett bizonyítani.
 

Megjegyzés. A feladat következő általánosítását tartalmazza Bollobás Béla dolgozata: Ha az ABCD négyszög AD és BC oldalát az M, illetőleg N pont m:n arányban osztja és
MN=m⋅DC+n⋅ABm+n,
(amit így szokás mondani: MN a DC és AB oldalnak m, illetőleg n súllyal súlyozott számtani közepe), akkor AB párhuzamos CD-vel, a négyszög trapéz. Az állítás az AC átlót m:n arányban osztó P pont segítségül vételével a fenti megoldáshoz hasonlóan bizonyítható.
 

3. feladat. Oldjuk meg a következő egyenletrendszert:
x+y=a(x-y)(1)x2+y2=a(x-y)2,(2)


ahol ,,a'' valós szám. ,,a'' mely értékeire lesznek valósak a gyökök ?
 

Megoldás. Az (1) és (2) egyenletekből
(x+y)2-(x2+y2)=(a2-a)(x-y)2,2xy=a(a-1)(x-y)2.(3)


Ezt felhasználva a (x-y)2 kifejezést fogjuk átalakítani. Tagokra bontva és (1)-et felhasználva
(x-y)2=x+y-2xy=a(x-y)-2xy.
A jobb oldal utolsó tagját (3) alapján így alakíthatjuk át:
2xy=4xy=2a(a-1)(x-y).(4)
Ezt behelyettesítve
(x-y)2=(a-2a(a-1))(x-y).
Innen, ha x-y≠0, akkor
x-y=a-2a(a-1),(5)
ha pedig x-y=0, akkor (2)-ből x=y=0 adódik, ami a tetszés szerinti értéke mellett megoldása az egyenletrendszernek. A továbbiakban csak az ettől különböző megoldásokat keressük.
Meg tudjuk határozni x-y-hoz hasonlóan x+y-t is, a négyzetét alakítva át (1), (4) és (5) felhasználásával:
(x+y)2=x+y+2xy=a(x-y)+2a(a-1)(x-y)==(a+2a(a-1))(a-2a(a-1))=a2-2a(a-1)=a(2-a).


Innen
x+y=a(2-a).(6)
(5) és (6)-ból
x=12(a(2-a)-2a(a-1)+a),(7)y=12(a(2-a)+2a(a-1)-a).(8)
Végül négyzetre emeléssel
x=14[a(2-a)+2a(a-1)+a2+2aa(2-a)-2a2a(a-1)--2a(2-a)2a(a-1)]==14(2a2+2aa(2-a)-2a2a(a-1)-2a(2-a)2a(a-1)),


azaz
x=12(a+a(2-a))(a-2a(a-1)).(9)
Ugyanígy nyerjük, hogy
y=12(a-a(2-a))(a-2a(a-1)).(10)

Ezek szerint csak (9) és (10) adhatja a feladat megoldását ‐ eltekintve x=y=0-tól ‐, feltéve, hogy értelemmel bír a valós számok körében, azaz sem a(2-a), sem 2a(a-1) nem negatív. Az első kifejezés a negatív és 2-nél nagyobb értékeire negatív, a második azokra, amelyekre 0<a<1. Így csak a=0 és 1≤a≤2 értékek jönnek tekintetbe. Az a=0 és a=2 értékre (9) és (10) a már tárgyalt x=y=0 megoldást adja, 1≤a<2-re ettől különböző értékpárokat. Az is világos, hogy az x-re és y-ra (amik (1) és (2)-ben négyzetgyökjel alatt is szerepelnek) kapott értékek nem negatívok, mert a x-re és y-ra kapott (7) és (8) kifejezések is valós számot adnak a szóba jövő a-értékekre, x és y pedig ezekből négyzetre emeléssel keletkezett.
Megmutatjuk még, hogy az x-re y-ra kapott kifejezések sem negatívok. Ekkor ezen kifejezéseket is felhasználva behelyettesítéssel könnyen látható, hogy (9) és (10) valóban megoldását adja az egyenletrendszernek. (7)-ből a
x=12(a(2-a)-2a(a-1)+a)=a2(a+2-a-2(a-1))
kifejezés a pozitív a+2-a+2(a-1)-gyel megszorozva a következőt kapjuk:
a2[(a+2-a)2-2(a-1)]=a2(a+2-a+2a(2-a)-2a+2)==a(a(2-a)+2-a).


Ez 1≤a<2-re pozitív, tehát (7) jobb oldala is. Hasonlóan (8)-ból
y(2-a+2(a-1)+a)=a2[(2-a+2(a-1))2-a]==a2(2-a+2a-2+22(2-a)(a-1)-a)=2a(2-a)(a-1)≥0,


ha 1≤a<2, tehát (8) bal oldala sem lehet negatív.
Ezzel beláttuk, hogy az (1), (2) egyenletrendszernek megoldása minden a mellett az x=y=0 értékpár. Ezen kívül 1≤a<2-re van megoldása, és azt a (7), (8) képletpár szolgáltatja.
 

Megjegyzések. 1. A közölt megoldás lényegében annak felel meg, hogy x+y és x-y helyett új változókat vezetünk be és először ezeket határozzuk meg.
2. Könnyen kiküszöbölhetjük az egyenletrendszerből a négyzetgyökös kifejezéseket, levonva a (2) a-szorosából (1) négyzetét:
a(x2+y2)-(x+y)2=a2(x-y)2-[a(x-y)]2=0,(a-1)x2-2xy+(a-1)y2=0.


Innen meghatározható az y/x hányados és ennek ismeretében (1)-ből x, majd y. Ezen az úton azonban kissé bonyolultabbak a számítások, mint a fenti megoldásban.