Cím: 1960. évi Kürschák József matematikai tanulóverseny feladatainak megoldása
Szerző(k):  Hajós György 
Füzet: 1961/március, 98 - 106. oldal  PDF  |  MathML 
Témakör(ök): Kürschák József (korábban Eötvös Loránd)

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Első feladat. Egy társasutazás bármely négy résztvevője között van olyan, aki a másik három mindegyikével már máskor is találkozott. Bebizonyítandó, hogy bármely négy résztvevő között van olyan, aki már minden útitársával találkozott.

 
Megjegyzés. A feladat csak arra az esetre vonatkozik, amikor a társasutazásnak van legalább négy résztvevője. Ha ez nem áll fenn, akkor a feladat feltevése és állítása egyaránt semmitmondó.
 
I. megoldás. Legyen A és B két olyan résztvevő, akik korábban még nem találkoztak. Feltehetjük, hogy van két ilyen, hiszen különben bármely résztvevő megfelelne a feladat kívánalmának. Azt is feltehetjük, hogy van az AB pártól különböző utaspár, akik szintén először találkoznak, mert különben minden A-tól és B-től különböző résztvevő megfelelne, és bármely négy résztvevő között van ilyen (sőt legalább kettő).
Az AB-től különböző, ugyancsak először találkozó utaspárban szerepelnie kell A-nak vagy B-nek, mert ha ez a CD utaspár A-tól és B-től különböző útitársakból állna, akkor A, B, C, D közül egyik sem találkozott volna korábban a másik három mindegyikével, és ez ellentmond a feladat feltevésének. Legyen tehát AC ez az AB-től különböző, ugyancsak először találkozó utaspár, hiszen minden lehetséges eset ezzé az esetté betűzhető át.
Azt vizsgáljuk most, hogy mely AB-től és AC-től különböző utaspár állhat olyanokból, akik máskor még nem találkoztak. Az előző bekezdés szerint A-nak vagy B-nek az ilyen utaspárban is szerepelnie kell, de ugyanolyan indokolással szerepelnie kell benne A és C valamelyikének is. Eszerint ez a további először találkozó utaspár csak BC vagy pedig AD lehet, ahol D egy még nem említett résztvevő.
Az utóbbi eset azonban lehetetlen, mert akkor az A, B, C, D résztvevőkre nem teljesülne a feladat feltevése. Eszerint az AB, AC párokon kívül csak BC állhat egymással először találkozó útitársakból, tehát minden A-tól, B-től és C-től különböző résztvevőnek találkoznia kellett már minden útitársával. Minthogy bármely négy résztvevő között van ilyen, a feladat állítása helyes.
 
Megjegyzés. Egyszerűbbé válik feladatunk megoldása, ha ábrázoljuk a vizsgált viszonyokat, és megfelelő elnevezéseket vezetünk be.
Ábrázoljuk a társasutazás résztvevőit egy-egy ponttal, és kössünk össze kettőt-kettőt közülük egy vonaldarabbal akkor, ha a két pontnak megfelelő útitárs korábban még nem találkozott. Az összekötő vonalakat úgy választjuk meg, hogy ne haladjanak át más résztvevőt ábrázoló ponton. Ilyen módon egy gráfhoz jutottunk, amelynek szögpontjai az útitársaknak, élei pedig az először találkozó utaspároknak felelnek meg. Ha a gráf élei esetleg metszik vagy érintik egymást, közös pontjukat nem számítjuk a gráf szögpontjai közé. Az általunk bevezetett gráfnak véges sok szögpontja van, minden éle két-két egymástól különböző szögpontot köt össze, és ugyanazt a szögpontpárt csak legfeljebb egy él köti össze. Ha a következőkben gráfról lesz szó, mindig csak ilyen gráfra gondolunk.
Ha feladatunkat a most bevezetett gráfra szövegezzük meg, a feladat a következő alakot ölti: Egy gráfnak nincs négy olyan szögpontja, amelyeknek mindegyikéből kiindul él a másik három szögpont valamelyikéhez. Bebizonyítandó, hogy a gráf bármely négy szögpontja között van olyan, amelyből nem indul ki él. Semmitmondó esetek kizárása kedvéért hozzátehettük volna, hogy a gráfnak legalább négy szögpontja van.
Az így szövegezett feladat megoldása rövidebb és áttekinthetőbb. Ezt a közölt megoldás átszövegezésén mutatjuk be:
Feltehetjük, hogy a gráfnak van legalább két éle, a és b, mert különben legfeljebb két szögpont kivételével egyikből sem indul ki él, és bármely négy szögpont között van ilyen. Az a, b élek egyik végpontja közös, mert különben négy végpontjukra nem teljesülne a feladat feltevése. Ebből az is következik, hogy az a, b éleken kívül csak olyan él szerepelhet, amelynek van közös pontja a-val is és b-vel is. Az ilyen él tehát (1. ábra) vagy a és b szabad végpontját köti össze, vagy pedig közös végpontjukból indul ki. Az utóbbi eset lehetetlen, mert akkor a három él négy végpontja ellentmondana a feladat feltevésének. Ezek szerint csak az a, b élek három végpontjából indul ki él, bármely négy szögpont között van tehát olyan, amelynek nincs meg ez a tulajdonsága.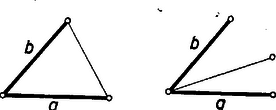
 
 
1. ábra
 

II. megoldás. Feltesszük, hogy van legalább négy olyan résztvevő, aki valamely útitársával a társasutazáson találkozik először, hogy tehát a feladat állítása nem teljesül, és bebizonyítjuk, hogy akkor a feladat feltevése sem teljesülhet, hogy tehát van négy olyan résztvevő, akik közül egyik sem találkozott korábban a másik három mindegyikével. Ez bizonyítja majd, hogy ha a feladat feltevése teljesül, állításának is teljesülnie kell.
Ismét abból indulunk ki, hogy A és B először találkozik egymással. Ha két tőlük különböző résztvevő korábban még nem találkozott, akkor máris találtunk az állításunkat bizonyító négy résztvevőt.
Legyen C és D két olyan további résztvevő, akik nem mindenkivel találkoztak korábban. Mostani feltevésünk szerint biztosan van két ilyen. Az előző bekezdés szerint csak azzal az esettel kell foglalkoznunk, amikor C is és D is csak már megbetűzött résztvevővel találkozik először. Ekkor azonban A, B, C és D négy olyan útitárs, akiknek egyike sem találkozott korábban a másik három mindegyikével, akik tehát állításunk helyességét bizonyítják.
 
Megjegyzések. 1. Második megoldásunk a gráfokra átültetett feladat szövegének további átfogalmazását teszi indokolttá. Ha a gráfból elhagyjuk azokat szögpontokat, amelyekből nem indul ki él, akkor a feladat következő megfogalmazásához jutunk: Egy gráf minden szögpontjából kiindul él, de nincs négy olyan szögpontja, amelyeknek mindegyikéből kiindul él a másik három valamelyikébe. Bebizonyítandó, hogy a gráfnak négynél kevesebb szögpontja van.
Ha ezt a feladatot ugyanúgy átszövegezzük, ahogyan az eredeti feladattal második megoldásunk elején tettük, akkor feladatunk következő újabb szövegéhez jutunk: Egy gráfnak legalább négy szögpontja van, és minden szögpontjából kiindul él. Bebizonyítandó, hogy van a gráfnak négy olyan szögpontja, amelyeknek mindegyikéből kiindul él a másik három valamelyikéhez. Az olvasóra hagyjuk, hogy második megoldásunkat e feladat megoldásává írja át.
2. Második megoldásunk mintájára bebizonyítjuk, hogy utolsó állításunk akkor is helyes, ha benne 4 helyett tetszőleges páros 2k természetes szám áll. Az általánosított feladat tehát a következőképpen szól: Egy gráfnak legalább 2k szögpontja van, és minden szögpontjából kiindul él. Bebizonyítandó, hogy van a gráfnak 2k olyan szögpontja, amelyeknek mindegyikéből kiindul él a többi 2k-1 szögpont valamelyikéhez.
Válasszunk ki gráfunkból lehetőleg sok független élt, azaz olyanokat, amelyeknek végpontjai mind különbözők. Ha van k független él, akkor ezek végpontjai máris bizonyítják állításunk helyességét. Ha csak j<k független élt választhattunk ki, ha tehát ezektől független (j+1)-edik él már nincs, akkor 2j végpontjukról tudjuk, hogy minden további szögpontból kiinduló él ennek a 2j végpontnak valamelyikébe fut. Ha tehát ehhez a 2j végponthoz bármely további 2k-2j szögpontot csatolunk, az állításunkat bizonyító 2k szögponthoz jutunk.
Megtehetnők, hogy a most bizonyított tényt annyiféleképpen fogalmazzuk át, ahányféleképpen ezt eredeti feladatunkkal megtettük. Megelégszünk azzal, hogy csak az eredeti megszövegezésbe öltöztetett eredményünket mondjuk ki: Ha egy társasutazás bármely 2k résztvevője között van olyan, aki a többi 2k-1 mindegyikével már máskor is találkozott, akkor bármely 2k résztvevő között van olyan, aki már minden útitársával találkozott. Semmitmondó eseteket zárunk ki, ha megköveteljük, hogy a társasutazásnak legalább 2k résztvevője van. Megemlítjük, hogy a k=1 esetben az állítás nyilvánvalóan helyes, a k=2 eset pedig eredeti feladatunk állítása.
3. Felmerül a kérdés, hogy helyes marad-e utolsó eredményünk, ha benne 2k helyett egy páratlan 2k+1 szám áll. Bebizonyítjuk, hogy így már hamis állításhoz jutunk, hogy tehát ez a módosítás az eddig említett különféle megszövegezések egyikénél sem megengedett. A 2k+1=1 esetet figyelmen kívül hagyjuk, mert ebben az esetben a feladat értelmét veszti.
Bizonyítás céljából elég egy kellően sok független élből álló gráfot tekintenünk. Ennek van legalább 2k+1 szögpontja, és minden szögpontjából kiinduló él. Nincs viszont 2k+1 olyan szögpontja, amelyek mindegyikéből kiindul él a többi 2k szögpont valamelyikébe. Akárhogyan szemelünk ki ugyanis 2k+1 szögpontot, az ezeket összekötő élek végpontjainak száma természetesen csak páros lehet, s így ezek nem meríthetik ki a 2k+1 szögpontot.
 
Második feladat. Az a1=1, a2, a3, ... természetes számok végtelen sorozatában
ak≤1+a1+a2+...+ak-1
minden k>1 értékre teljesül. Bebizonyítandó, hogy minden természetes szám felírható ebből a sorozatból kiválasztott számok összegeként (vagy pedig előfordul a sorozatban).
 
Megjegyzés. A feladat zárójeles toldaléka felesleges akkor, ha egytagú összeget is lehetségesnek tartunk, ha tehát bármely számot a saját összegének is mondunk. Ez a felfogás megkönnyíti a szövegezést, a megoldásainkban szereplő összegek is így értendők.
 
I. megoldás. A feladat állításán túlmenően azt bizonyítjuk, hogy ha 0<n≤a1+a2+...+ak, akkor az n természetes szám felírható a véges a1,a2,...,ak sorozatból kiválasztott számok összegeként. Ezt az állítást k-ra vonatkozó teljes indukcióval bizonyítjuk be.
Ha k=1, akkor állításunk a1=1 miatt helyes, hiszen ebben az esetben csak n=1 lehetséges. Legyen tehát k>1, és tegyük fel, hogy állításunk helyes, ha benne k helyén k-1 áll.
Ha 0<n≤a1+a2+...+ak-1, akkor indukciós feltevésünk szerint n felírható a kívánt alakban, ti. már a1,a2,...,ak-1 is elegendő az összegül n-et adó számok kiválasztásához. Legyen tehát
1+a1+a2+...+ak-1≤n≤a1+a2+...+ak.
Minthogy a baloldali összeg a feladat feltevése szerint legalább ak, egyenlőtlenségeinkből
0≤n-ak≤a1+a2+...+ak-1
következik. Eszerint n-ak vagy 0, vagy pedig az indukciós feltevés szerint felírható az a1,a2,...,ak-1 sorozatból kiválasztott számok összegeként. Így tehát vagy n=ak, vagy pedig ak-t a kiválasztott számokhoz csatolva összegül n adódik.
 
II. megoldás. Ismét azt bizonyítjuk, hogy ha 0<n≤a1+a2+...+ak, akkor n felírható az a1,a2,...,ak sorozatból kiválasztott számok összegeként, de most n-re vonatkozó teljes indukciót alkalmazunk.
Ha n=1, akkor a1=1 miatt helyes az állítás, akármekkora is k értéke. Legyen tehát n>1, és tegyük fel, hogy állításunk helyes, ha benne n helyén nála kisebb m szám áll.
A rögzített n>1 mellett olyan k értékeket kell tekintenünk, amelyekre n≤a1+a2+...+ak teljesül. Elég, ha közülük csak a legkisebbel foglalkozunk, tehát azzal a k értékkel, amelyre
a1+a2+...+ak-1<n≤a1+a2+...+ak,
hiszen k növelésekor az összegül n-et adó számok kiválasztásához rendelkezésre álló választék csak növekszik.
Egyenlőtlenségeinkből az m=a1+a2+...+ak-n értékre 0≤m<ak adódik. Így tehát a feladat feltevését is alkalmazva
0≤m≤ak-1≤a1+a2+...+ak-1<n.
Ha tehát az érdektelen m=0 (azaz n=a1+a2+...+ak) esetet figyelmen kívül hagyjuk, akkor
0<m<n≤a1+a2+...+ak.
Indukciós feltevésünk szerint ez éppen azt biztosítja, hogy m előállítható az a1,a2,...,ak sorozatból kiválasztott számok összegeként. Ha tehát ezeket ebből a sorozatból elhagyjuk, akkor a megmaradóknak n az összege.
 
Megjegyzések. 1. Felvethető a kérdés, hogy feladatunk feltevésének teljesülnie kell-e, ha állítása teljesül. Ez nincs így. Ha pl. minden i≠2 esetben ai=1, viszont a2=3, akkor a feltevés a k=2 esetben nem teljesül: 3>1+1, viszont bármely természetes szám mégis előállítható az 1, 3, 1, 1, 1, ... sorozatból kiválasztott számok összegeként.
Elmondhatjuk, hogy negatív tapasztalatunk nem meglepetés, mert a végtelen sorozat elemeinek permutálása a természetes számok előállíthatóságának mit sem árt, viszont megszüntetheti a feladat feltevésének teljesülését. Előző példánk is úgy keletkezik, hogy a feltevést is kielégítő 1, 1, 3, 1, 1, 1, ...sorozat két elemét felcseréljük.
2. Feladatunk feltételének szükségességét mégiscsak bebizonyítjuk, de a következő formában: Ha minden természetes szám felírható egy természetes számokból alakuló c1,c2,c3,... végtelen sorozatból kiválasztott számok összegeként, akkor ez a sorozat átrendezhető a1=1,a2,a3,... alakba úgy, hogy
ak≤1+a1+a2+...+ak-1
minden k>1 értékre teljesüljön.
Abból indulunk ki, hogy a1=1 lehetséges választás, hiszen 1-nek szerepelnie kell a c1,c2,c3,... sorozatban, mert 1 is előállítható általa. A további ai értékek megválasztását a következőképpen szabályozzuk:
Minthogy N2=2 előállítható, a c1,c2,c3,... sorozatban a1 elhagyása után is szerepelnie kell legalább egy N2-nél nem nagyobb elemnek (ti. 1-nek vagy 2-nek). Azt választjuk közülük a2-nek, amelyiknek a c1,c2,c3,... sorozatban a legkisebb az indexe.
a2 megválasztása után van egy legkisebb N3 természetes szám (ti. 3 vagy 4), amely nem írható fel a véges a1, a2 sorozatból kiválasztott számok összegeként. Szerepelnie kell ezért a c1,c2,c3,... sorozatban a1 és a2 elhagyása után is legalább egy N3-nál nem nagyobb számnak. Azt választjuk közülük a3-nak, amelyiknek az indexe a c1,c2,c3,... sorozatban a legkisebb.
Így folytatjuk ezt az eljárást. Ha már megválasztottuk az a1,a2,...,ak-1 sorozatelemeket, akkor van egy legkisebb Nk természetes szám, amely nem írható fel a véges a1,a2,...,ak-1 sorozatból kiválasztott számok összegeként. Szerepelnie kell ezért a c1,c2,c3,... sorozatban a már kiválasztott elemek elhagyása után legalább egy Nk-nál nem nagyobb számnak. Ezek közül azt választjuk ak-nak, amelyiknek az indexe a c1,c2,c3,... sorozatban a legkisebb.
A következő lépésben fellépő Nk+1 nagyobb Nk-nál, hiszen Nk maga már bizonyosan felírható az a1,a2,...,ak sorozatból kiválasztott számok összegeként vagy azért, mert ak=Nk, vagy pedig azért, mert ak mellé az a1,a2,...,ak-1 sorozatból Nk-ak összeget adó számokat választhatunk ki, hiszen Nk volt a legkisebb így elő nem állítható szám.
Ha tehát eljárásunkat minden határon túl folytatjuk, akkor N2<N3<N4<... miatt a c1,c2,c3,... sorozat bármely ci eleme előbb-utóbb kiválasztásra kerül, mert ha pl. a k-adik lépésben már Nk≥ci, akkor ettől a lépéstől kezdve csak ci vagy nála kisebb indexű elem kerülhet kiválasztásra, márpedig a véges sok c1,c2,...,ci-1 elem előbb-utóbb elfogy. Ezek szerint az általunk képezett a1,a2,a3,... sorozatban a c1,c2,c3,... sorozat minden eleme előfordul, tehát az utóbbi sorozatot valóban átrendeztük.
Nk definíciójából következik, hogy értéke legfeljebb 1+a1+a2+...+ak-1 hiszen ez a szám biztosan nem állítható elő az a1,a2,...,ak-1 sorozatból kiválasztott számok összegeként. Minthogy pedig ak≤Nk, bebizonyítottuk, hogy feladatunk feltevésének teljesülnie kell az átrendezéssel származtatott a1,a2,a3,... sorozatra.
3. Ha az a1≤a2≤a3≤... feltételnek eleget tevő monoton sorozatokra szorítkozunk, akkor kizártuk azt, hogy a sorozat elemeit permutálhassuk, hogy tehát a feladat feltevésének teljesülése ettől a permutálástól függjön. Az ilyen monoton sorozat esetében a feladat feltevésének (minden permutálás nélkül) teljesülnie kell, ha az állítása teljesül.
Ha ugyanis ak>1+a1+a2+...+ak-1=n, akkor n nem írható fel az a1,a2,a3,... sorozatból kiválasztott számok összegeként, hiszen ebben a végtelen sorozatban csak az a1,a2,...,ak-1 elemek nem nagyobbak n-nél, és mindezeknek az összege még mindig kisebb nála.
4. Utolsóként azt a kérdést vetjük fel, hogy hogyan kell a feladat feltevését kielégítő sorozatot megválasztani, ha azt akarjuk, hogy elemei a lehető legnagyobbak legyenek. Megmutatjuk, hogy 1, 2, 4, 8, ... ez az optimális sorozat.
Akárhogyan választjuk meg ugyanis a feltevést kielégítő sorozatot, ebben minden k>1 értékre teljesül az
ak≤2k-1
egyenlőtlenség. Ezt k-ra vonatkozó teljes indukcióval bizonyítjuk be. A k=2 esetben helyes az állítás, mert a feltevés szerint a2≤1+a1=21. Legyen tehát k>2, és tegyük fel, hogy az állítás teljesül, ha benne k helyén nála kisebb szám áll. Ekkor
ak≤1+a1+a2+...+ak-1≤1+20+21+...+2k-2=2k-1,
ami állításunk helyességét bizonyítja.
Az utolsó egyenlőség, éppen feladatunk állítására hivatkozva, azt a jól ismert tényt bizonyítja, hogy minden természetes szám felírható 2 különböző hatványainak összegeként. Beláttuk tehát, hogy a vizsgált tulajdonságú sorozatok közül 2 hatványsorozatának az elemei a legnagyobbak.
 
Harmadik feladat. Az ABCD négyzet AB oldalát az E pont felezi, a BC és a CD oldalon pedig úgy helyezkednek el az F, G pontok, hogy az AG, EF egyenesek párhuzamosak. Bebizonyítandó, hogy az FG szakasz érinti a négyzetbe írt kört.
I. megoldás. Ha a CFG▵-höz írt, az FG oldalt kívülről érintő kör ezt az oldalt H-ban, a CF, CG oldalak meghosszabbítását pedig a J, K pontokban érinti (2. ábra), akkor ez utóbbiakra
CJ=CKésFJ+GK=FG,(1)
hiszen az egy pontból ugyanahhoz a körhöz vont érintőszakaszok egyenlők, s ezért FJ=FH és GK=GH.
 
 
2. ábra
 

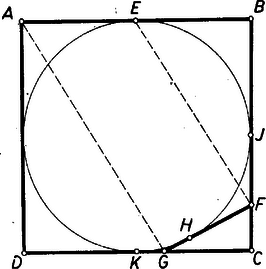Azt állítjuk, hogy (1) a CF, CG oldalak meghosszabbításain elhelyezkedő pontpárok közül csak a szóban forgó érintési pontokra teljesül. Ha ugyanis a J, K pontokat elmozgatva növeljük vagy csökkentjük a CJ=CK távolságot, akkor FJ+GK is növekszik vagy csökken, tehát már nem lehet FG-vel egyenlő.
Ezek szerint elég azt bizonyítanunk, hogy a négyzet BC, CD oldalainak J, K felezőpontjaira (1) teljesül, mert ebből következik, hogy a J, K pontokban érintő, tehát a négyzetbe írt kör érinti az FG oldalt is. Felhasználtuk itt azt, hogy J és K a CF, CG szakaszok meghosszabbításán van. Ez abból következik, hogy AC∥EJ és AK∥EC, s ezért a DGC sorrendből a CFJ sorrend, a BFC sorrendből pedig a CGK sorrend következik.
Legyen a négyzet oldala 2, azaz válasszuk hosszegységül az oldalhossz felét. Ha tehát DG=x, akkor
CG=2-x,GK=x-1.
Az ADG, FBE háromszögek hasonlók, mert oldalaik párhuzamosak. Ezért 2:x=FB:1, tehát FB=2/x, és így
CF=2-2x,FJ=2x-1.
Minthogy (FJ+GK)2=FG2 bizonyítására van szükségünk, Pythagoras tétele szerint már csak
[(2x-1)+(x-1)]2=(2-2x)2+(2-x)2
helyességét kell belátnunk. Ez valóban helyes, hiszen a bal oldal
(2x-2+x)2=(2x-2)2+2x(2x-2)+x2
alakban írható, s itt az utolsó két tag együttes értéke 4-4x+x2=(2-x)2.
 
II. megoldás. Ha a derékszögű CFG▵-höz írt, az FG átfogót kívülről érintő kör középpontja O (3. ábra), akkor
FOG∢=45∘,(2)
hiszen OF és OG felezi az egymást derékszöggé kiegészítő JOH, HOK szögeket, ahol H, J, K az előző megoldásban bevezetett pontok.
 
 
3. ábra
 

Azt állítjuk, hogy (2) az FCG derékszög szögfelezőjén elhelyezkedő pontok közül csak a szóban forgó középpontra teljesül. Ha ugyanis O a szögfelezőn elmozdulva közeledik a szögfelezőt metsző FG szakaszhoz, vagy távolodik tőle, akkor az FOG látószög növekszik, illetőleg csökken.
Ezek szerint elég azt bizonyítanunk, hogy (2) a négyzet O középpontjára teljesül, tehát azt, hogy
FOG∢=GDO∢.(3)
E szögek közül az elsőt a GOD, FOB szögek, a másodikat a GOD, OGD szögek 180∘-ra egészítik ki. Ezért (3) igazolásához csak
FOB∢=OGD∢(4)
bizonyítására van szükség.
Ennek bizonyításához abból indulunk ki, hogy az ADG, FBE háromszögek hasonlósága miatt DG:2a=a:BF, ahol 2a a négyzet oldalhossza. Eszerint DG⋅BF=2a2, vagyis DG:DO=BO:BF, hiszen DO=BO=a2. Ebből az aránypárból következik azonban, hogy GDO▵∼OBF▵, hiszen ezekben a háromszögekben GDO∢=OBF∢=45∘. A hasonlóság miatt a két háromszög megfelelő szögei egyenlők, tehát (4) valóban teljesül.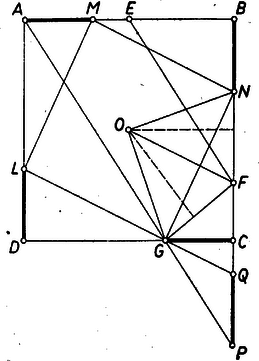
 
III. megoldás. Mérjük fel négyzetünk négy oldalára a CG=DL=AM=BN szakaszokat (4. ábra). A forgásszimmetria miatt GLMN is négyzet. Messék az AG, LG egyenesek a BC egyenest a P, Q pontokban. Minthogy az ALDG pontnégyes a szerkesztés révén hasonló a PQCG pontnégyeshez, és az előbbiben AL=DG, azért a másik pontnégyes megfelelő pontjaira PQ=CG. Így tehát PQ=BN.
 
 
4. ábra
 

Minthogy EF az APB▵ középvonala, F felezi a PB szakaszt, tehát az ezen belül szimmetrikusan elhelyezkedő QN szakaszt is. Eszerint F a derékszögű QNG▵ átfogójának felezőpontja, egyenlő távolságra van tehát e háromszög csúcsaitól, azaz FG=FN. Ebből következik, hogy OFG▵≃OFN▵, hiszen a forgásszimmetria miatt OG=ON, tehát a két háromszög oldalai páronként egyenlők. A bizonyított egybevágóságból következik, hogy az O pont az FG, FN egyenesektől egyenlő távolságra van, hogy tehát a négyzetbe írt kör az FG szakaszt is érinti.
 
IV. megoldás. Ha az F pontot ismerjük, akkor az AG∥EF előírás egyértelműen meghatározza a G pontot. Ha F-ből a négyzetbe írt körhöz második érintőt vonunk, akkor ez a CD oldalból F által ugyancsak egyértelműen meghatározott pontot metsz ki. Feladatunk azt állítja, hogy ez a két hozzárendelés azonos. Ezt most úgy bizonyítjuk, hogy a négyzetbe írt kört érintő FG szakaszból indulunk ki, és megmutatjuk, hogy AG∥EF.
Tekintsük a négyzetbe írt kör mellett a CFG▵-höz írt, a CF oldalt kívülről érintő kört (5. ábra). Érintse ez a CD egyenest az R pontban. F a két kör belső hasonlósági pontja, hiszen közös belső érintőik metszéspontja. Ebből következik, hogy a két kört ellentétes oldalról érintő és párhuzamos AB, DC egyenesek E, R érintési pontjai a hasonlóság által egymáshoz rendelt pontok, hogy tehát az E, F, R pontok egy egyenesen vannak.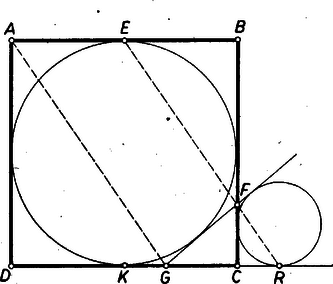
 
 
5. ábra
 

Azt kell bizonyítanunk, hogy AG párhuzamos EF-fel, azaz ER-rel; tehát azt, hogy AERG parallelogramma. Ehhez GR=AE bizonyítására van szükség. Ez viszont következik abból, hogy egyrészt AE=KC, ahol K a CD oldal felezőpontja, másrészt pedig GR=KC is teljesül, hiszen ismeretes, hogy egy háromszög valamely oldalának két meghosszabbítását a háromszöghöz írt körök az oldalhoz viszonyítva szimmetrikusan elhelyezkedő pontokban érintik.
 
Megjegyzések. 1. Harmadik feladatunk állítása akkor is helyes, ha benne nem a BC, CD oldalakon, hanem a BC, CD oldalegyeneseken elhelyezkedő pontokról szólunk, és nem az FG szakaszról, hanem az FG egyenesről állítjuk, hogy érinti a négyzetbe írt kört. Harmadik megoldásunk közvetlenül alkalmas ennek bizonyítására is, a többinél pedig csekély módosításra van ehhez szükség. Az olvasóra hagyjuk, hogy ezeket a módosításokat megkeresse.
2. Akkor is helyes marad feladatunk állítása, ha nem négyzetről, hanem rombuszról szólunk, és E nem az AB oldal felezőpontját, hanem a rombuszba írt kör és az AB oldal érintési pontját jelenti. Negyedik megoldásunk közvetlenül alkalmazható ennek a bizonyítására is.
A rombuszra kimondott állítás szintén helyes marad, ha a BC, CD, FG szakaszok szerepét e szakaszok egyenesei veszik át. A negyedik megoldás az előbb már említett módosítás után ezt is bizonyítja.
3. Pusztán megemlítjük, hogy harmadik feladatunk állítását nagyon gyorsan bizonyíthatja, aki ismeri a kúpszeletek érintőiről szóló Brianchon-tételt, s hogy ez a rövid bizonyítás az előbb említett általánosítások mindegyikét közvetlenül bizonyítja. A részletekbe itt nem bocsátkozhatunk, mert ehhez a középiskolai anyagot messze meghaladó ismeretekre volna szükség.