Cím: Az 1960. évi Arany Dániel tanulóversenyek II. fordulóján kitűzött feladatok megoldása (2. közlemény) Haladók (II. osztályosok) versenye
Szerző(k):  Lőrincz Pál ,  Surányi János 
Füzet: 1961/január, 1 - 6. oldal  PDF  |  MathML 
Témakör(ök): Arany Dániel

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Haladók (II. osztályosok) versenye.
1. feladat. Egy derékszögű háromszög oldalainak mértékszámai egész számok. A háromszög területe mértékszámának kétszerese egyenlő a kerület mértékszámának háromszorosával. Mekkorák a háromszög oldalai ?

 

I. megoldás: Jelöljük a háromszög befogóit a és b-vel, átfogóját c-vel. Feltehetjük, hogy a<b, ugyanis az egyenlő szárú derékszögű háromszögnek nem lehet mind a három oldala egész szám. Pythagorász tétele szerint
a2+b2=c2,(1)
a feladat követelménye szerint pedig
ab=3(a+b+c).(2)
Meg kell határoznunk az (1), (2) egyenletrendszer pozitív egész megoldásait, azaz meg kell oldanunk ezen diophantoszi egyenletrendszert. Ebben eljárhatunk úgy, hogy kiküszöböljük c-t, így egyetlen, az a és b-ben szimmetrikus diophantoszi egyenletre jutunk ‐ ugyanis (1) és (2) mindegyike a és b-ben szimmetrikus ‐, ezt megoldjuk, majd a megoldások közül kiválasztjuk azokat, amelyekhez (1) vagy (2) szerint tartozó c szintén egész szám. (2)-ből
c=ab3-a-b,(2a)
ezt (1)-be helyettesítve, a törtek eltávolításával
9(a2+b2)=a2b2+9a2+9b2-6a2b-6ab2+18ab,
majd rendezés után ab-vel végigosztva (ugyanis a, b≠0) az egyenletet így alakíthatjuk:
(a-6)(b-6)=18.(3)

a és b-vel együtt a bal oldal tényezői egészek. A jobb oldali szám hatféleképpen bontható fel két egész szám szorzatára:
1⋅18,2⋅9,3⋅6,továbbá(-1)⋅(-18),(-2)⋅(-9),(-3)⋅(-6).
Mivel azonban a és b pozitívok, tehát a-6 és b-6 mindegyike nagyobb -6-nál, és ezt a követelményt 18 negatív egész tényező párjai közül egyik sem teljesíti egyidejűleg mindkét tényezőre, azért csak a pozitív tényezőkre bontások felelnek meg. Ezek szerint (3)-nak három megoldása van:
a-6=11,12,13,ésb-6=18,19,16-ból:a=17,18,19,ésb=24,15,12.

Mivel 18-cal együtt az a-6 és b-6 tényezőknek legalább az egyike osztható 3-mal, azért ugyanez áll a 6-tal nagyobb a és b-re és következésképpen szorzatukra is, ennélfogva a (2a)-ból kiszámítható c mindhárom esetben egész szám:
c=25,17,15.

Ezek szerint a követelményeknek három háromszög felel meg.
 

Megjegyzés. Néhány versenyző indokolatlanul feltételezte, hogy a keresett háromszög oldalainak aránya 3:4:5. Miután a megoldások között ilyen is van, így véletlenül ebből az alaptalan feltevésből is rá lehetett jutni egy megoldásra, de nem mindre.
 

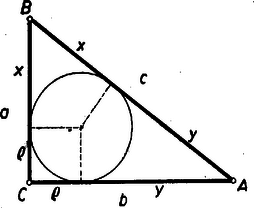
II. megoldás: Ismeretes, hogy minden háromszög területe t=ϱ⋅s alakban írható, ahol ϱ a háromszög beírt körének sugara, és s a háromszög félkerülete. Így a keresett háromszögre nézve 2ϱs=3⋅2s, és innen, mivel s nem lehet 0, ϱ=3, egész szám.
A beírt kör érintési pontjai az oldalakat úgy osztják két-két részre, hogy a csúcsokban összefutó részek páronként egyenlők. A derékszög csúcsában összefutó két rész hossza ϱ, mert e részek és a végpontjaikhoz tartozó sugarak által alkotott négyszögben három derékszög van, és két szomszédos oldal egyenlő, tehát az idom négyzet. Eszerint, az átfogó két szakaszát x, y-nal jelölve az oldalak rendre: a=ϱ+x=3+x, b=ϱ+y=3+y, c=x+y tehát x=a-3, y=b-3 egész számok.
 
 

Pythagorász tételével
(3+x)2+(3+y)2=(x+y)2,
ezt az egyenletet a következő alakra hozhatjuk:
(x-3)(y-3)=18.(4)
Eszerint ismét 18 egész tényező párokra bontásai vezetnek megoldáshoz. A beírt kör középpontja, a befogókon levő érintési pontok és az átfogó végpontjai által meghatározott derékszögű háromszögekből látható, hogy az x, y befogók nagyobbak ϱ-nál, mert velük szemben nagyobb szög fekszik. Ugyanis e háromszögek ϱ-val szemben fekvő szögei fele akkorák, mint az eredeti háromszög hegyes szögei, tehát kisebbek 45∘-nál. Eszerint x, y>ϱ=3, így x-3, y-3 pozitívok és a<b-re tekintettel x-3<y-3. Így 18-nak ismét csak a pozitív tényezőkre való felbontásai jönnek szóba:
a=x+3=(x-3)+6esx-3=11,12,13,a=x+3=(x-3)+6ésy-3=18,19,16-ból,a=x+3=(x-3)+6esy-3=17,18,19,b=y+3=(y-3)+6esy-3=24,15,12,c=x+y=(x-3)+(y-3)+6=25,17,15,
ismét az I. megoldásban nyert háromszögekre jutottunk.
 

Megjegyzés. A kitűzött feladat speciális esete a következő feladatnak: Egy derékszögű háromszög oldalainak mértékszámai egész számok. A háromszög területe mértékszámának kétszerese egyenlő a kerület mértékszámának ϱ-szorosával, ahol ϱ adott pozitív egész szám. Mekkorák a háromszög oldalai ? (Esetünkben ϱ=3 volt.) A követelmény szerint a 2t:2s arány értéke ϱ, az ezzel egyenlő t:s arány viszont ‐ mint láttuk ‐ a beírt kör sugarát adja meg, ennélfogva a ϱ szám minden megoldásban a beírt kör sugarának mértékszáma. Ebből a II. megoldás gondolatmenetével (4) helyett az
(x-ϱ)(y-ϱ)=2ϱ2x,y>ϱ(5)
diophantoszi egyenletre jutunk. Ebből annyi megoldást nyerünk, ahányféleképpen 2ϱ2-et két pozitív egész tényező szorzatára lehet bontani, ugyanis ϱ, x-ϱ, y-ϱ-val együtt x, y, a=x+ϱ, b=y+ϱ és c=x+y szintén egész számok.
Érdekes, hogy ϱ minden értéke mellett van olyan megoldás, melyben az oldalak aránya 3:4:5. Erre vezet ugyanis 2ϱ2-nek ϱ⋅2ϱ alakú felbontása: x-ϱ=ϱ, y-ϱ=2ϱ-ból x=2ϱ, y=3ϱ és a=3ϱ, b=4ϱ, c=5ϱ.
 

III. megoldás: Ismeretes, hogy az (1) pythagorászi egyenletet kielégítő a, b, c egész számhármasokat pythagorászi számhármasoknak szokás nevezni. Az ilyeneknek minden λa, λb, λc többszöröse ‐ ha λ pozitív egész szám ‐ ugyancsak pythagorászi számhármas. Ha a és b relatív prímek, akkor c és a, továbbá c és b szintén relatív prímek, ilyen esetben a, b, c-t alaphármasnak nevezzük. Ismeretes az is, hogy minden alaphármas kifejezhető két u, v paraméterrel a következőképpen:
a=u⋅v,b=u2-v22,c=u2+v22,(6)
ahol u és v pozitív egész, páratlan relatív prim számok. * Ezekkel minden pythagorászi számhármas így írható:
a=λ⋅u⋅v,b=λ⋅u2-v22,c=λ⋅u2+v22,(7)
ugyanis minden pythagorászi számhármas valamely alaphármas többszöröse.
Feladatunk most már a (7) közül kiválasztani a (2)-nek eleget tevő számhármasokat. (Az a<b követelményt a továbbiakban természetesen nem tarthatjuk fenn, mert a és b kifejezése lényegesen különböző.) E kifejezéseket (2)-be beírva b+c=λu2 alapján a
λ2uv(u-v)(u+v)=6λu(v+u)
egyenletre jutunk. Ezt λ-val, u-val és u+v-vel oszthatjuk, mert egyikük se 0:
λv(u-v)=6.

A bal oldal tényezői közül v páratlan, u-v páros, és λ tetszőleges pozitív egész. Másrészt 6=2⋅3=1⋅2⋅3, így a tényezők megfeleltetésére a következő lehetőségek vannak:
v=1,3,u-v=2,6︷,2,

ekkor
u-v-vλ=3,1,1,

és
u-v-vu=3,7,5,

ennélfogva (7) szerint
u-v-va=9,7,15,u-v-vb=12,24,8,u-v-vc=15,25,17,
Ismét az előzők során nyert háromszögekhez jutottunk. Látjuk továbbá a λ=1 értékből, hogy a második és a harmadik megoldás alaphármas. Valóban, a 7, 24, 25 és a 15, 8, 17 számok páronként relatív prímek, az első hármas viszont λ=3-szorosa a 3, 4, 5 alaphármasnak.
 

2. feladat. Az ABCD rombusz középpontjából az AB oldalra bocsátott merőleges talppontja T, a D csúcsból az ugyancsak AB oldalra bocsátott merőleges talppontja U, a DU szakasz felezőpontja F. Bizonyítsuk be, hogy BF merőleges TC-re !
 

Megoldás: A rombusz természetesen úgy értendő, hogy a csúcsok a felsorolás sorrendjében következnek a kerület mentén; különben a feladat állítása nem is igaz.
 

 
 

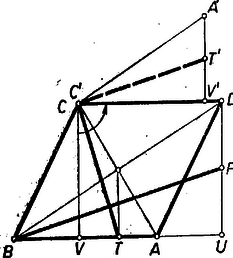
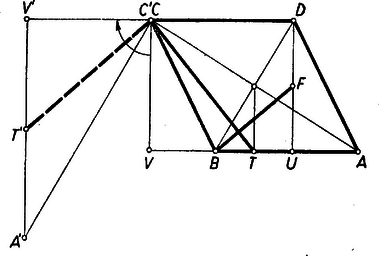
Bocsássunk C-ből is merőlegest AB-re, és legyen ennek talppontja V. Forgassuk el az ACV háromszöget (egy tetszés szerinti pont körül bármelyik irányban) 90∘-kal. Ekkor CV egy az AB-vel (s így egyszersmind BU-val is) párhuzamos C'V' helyzetbe kerül; AV egy AB-re merőleges, tehát DU-val párhuzamos helyzetbe megy át, AC elforgatott helyzete, A'C' pedig AC-re merőleges, tehát BD-vel párhuzamos lesz. Így az A'C'V' háromszög hasonló helyzetű a DBU háromszöghöz. Ekkor bennük bármely két megfelelő egyenes is párhuzamos, többek közt a C'-t és a neki megfelelő B csúcsot a szemközti oldal T', ill. F felezőpontjával összekötő egyenesek is. Itt C'T' a CT elforgatott helyzete, tehát merőleges CT-re, s így merőleges rá BF is. Ezt kellett bizonyítanunk.
 

3. feladat. Oldjuk meg az
x(x+2)(x+3)(x+5)+8=0(1)
egyenletet !
 

I. megoldás: Észrevehetjük, hogy a szorzat első és negyedik tényezőjének számtani közepe egyenlő a második és harmadik tényező számtani közepével, x+52-del. Tekintsük ezt új ismeretlennek, legyen tehát
x+52=z,azazx=z-52,(2)
így a
(z-52)(z-12)(z+12)(z+52)+8=(z2-254)(z2-14)+8=0,
azaz
z4-132z2+15316=0
egyenletre jutunk. Kiszámítva a gyököket, majd (2) szerint az ezekhez tartozó x értékeket:
13+1z1=172,x1=17-52,z2=134±1z2=-172,x2=-17-52,13+1z3=32,x3=-1,13+1z4=-32,x4=-4,
az egyenletet megoldottuk. Látjuk, hogy mind a négy gyök valós.
 

II. megoldás: Vegyük észre, hogy (1) első tagjában az első és negyedik tényező szorzata a második és harmadik tényező szorzatától csak állandóban különbözik. Egyenletünk tehát ilyen alakúra hozható:
(x2+5x)(x2+5x+6)+8=0.
Vegyük új ismeretlennek az új első tényezőt:
x2+5x=w,(3)
így a
w(w+6)+8=0
egyenletre jutunk, melynek gyökei:
w1=-2,w2=-4.
Ezeket rendre (3)-ba helyettesítve nyerjük, hogy a w1-hez tartozó két x gyök éppen az I. megoldás során nyert x1 és x2, míg a w2-höz tartozó két gyök a fenti x3 és x4-gyel egyezik meg.
 

Megjegyzések. 1. Minden
(x+a)(x+b)(x+c)(x+d)+e=0
alakú egyenlet megoldható akár az I., akár a II. megoldásban alkalmazott helyettesítéssel, hacsak az a, b, c, d számok két egyenlő összegű párba kapcsolhatók, pl.
a+b=c+d.

2. Az adott egyenlet elég egyszerű ahhoz, hogy az egész gyökökre némi próbálgatással is rá lehessen jutni. Azonban maga az a feltevés, hogy a gyökök egész számok, általában indokolatlan, hiszen pl. az
x(x+2)(x+3)(x+5)+10=0
egyenletnek egyik gyöke sem egész, sőt még csak nem is valós, amiről könnyen meggyőződhetünk, ha a gyököket akár az I., akár a II. megoldásban alkalmazott helyettesítéssel kiszámítjuk. Annyi mindenesetre látható az (1)-beli szorzaton, hogy x nem lehet (racionális) tört, mert x=p/q-val ‐ ahol p és q relatív prím egészek, q>1 ‐, mind a négy tényező tört, és nevezője q, márpedig egyenlő nevezőjű nem egyszerűsíthető törtek szorzata nem lehet egész.
*Hasonló, még ismertebb kifejezések a következők:
a=u2-v2,b=2uv,c=u2+v2,
ahol u, v relatív prim pozitív egész számok, u>v, egyikük páros, másikuk páratlan. Ezt lásd pl: Rademacher‐Toeplitz: Számokról és alakzatokról, Középiskolai Szakköri Füzetek, Tankönyvkiadó, 1954. 84. o.