Kezdőlap


Cím:	A sík lefedése egybevágó konvex sokszögekkel 2.
Szerző(k):	Bollobás Béla
Füzet:	1961/május, 193 - 200. oldal	PDF \| MathML
Témakör(ök):	Szakmai cikkek

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

(2. befejező közlemény)
Az egyenletes ötszögparkettázsok

A lefedéssel szemben újabb követelményeket támasztva további érdekes eredményeket kaphatunk: a sokszög alakjára vonatkozó elégséges feltételeket ahhoz, hogy a sokszögből parkettázst készíthessünk.
Nevezzük egyenletesnek az olyan másodfajú lefedést, melyben bármely

A

és

B

sokszöghöz tartozik olyan egybevágósági transzformáció (ez tengelyes tükrözés is lehet), mellyel

A

B

-be kerül s az

A

-val együtt mozgatott parkettázs élei egybeesnek az eredeti parkettázs éleivel.
Ezek elég erős kikötések, mind a fedősokszög alakját, mind a lerakási módot korlátozzák. Több olyan parkettázs nem minősül egyenletesnek, amely egyébként számos szabályszerűséget mutat, pl. a 2., 5. ábrák. Nyilvánvaló viszont, hogy a 3., 6. és 7. ábrák parkettázsai egyenletes lefedések. Megjegyezzük, hogy az egyenletes parkettázs feltételei a három- és négyszögparkettázsok esetében a sokszögek alakját nem korlátozzák. Minden három- és négyszögből lehet készíteni egyenletes lefedést, sőt a tetszőlegesen felvett négyszögből (melyről csak azt használhatjuk ki, hogy négy oldala van, nem hurkolt és belső szögeinek összege

360^{\circ}

) csak egyenletes parkettázs készíthető.
A következőkben megvizsgáljuk, hogy milyen konvex ötszögekből készíthető egyenletes lefedés.
Először meghatározzuk, hogy az ötszögcsúcsokból, mint csomókból hány él indulhat ki. Tekintsünk egy egyenletes ötszögparkettázst, jelöljük valamely ötszögének csúcsaiból, mint csomópontokból kiinduló élek számát (valamilyen sorrendben)

e_{1}

e_{2}

e_{3}

e_{4}

e_{5}

-tel (az alapötszög éleit is beleszámítva). E számok között természetesen egyenlők is lehetnek. Jelöljük az

e_{1}, ..., e_{5}

számok közül

e_{1}

-gyel egyenlők számát ‐ ebbe

e_{1}

-et is beleszámítva ‐

k_{1}

-gyel, az

e_{2}

-vel egyenlők számát

k_{2}

-vel,

...

, az

e_{5}

-tel egyenlők számát

k_{5}

-tel. ¹
A meghatározásból következik, hagy az egyenletes parkettázs minden ötszögének megfelelő csúcsaiból, mint csomópontokból rendre

e_{1}

e_{2}

e_{3}

e_{4}

e_{5}

él indul ki. Alkalmazzuk az V. tétel bizonyításának módszerét és jelöléseit, továbbá jelöljük az

a

oldalú négyzetben levő

e_{i}

élű csomók számát

c_{i}

-vel (

i = 1, 2, 3, 4, 5

), az összes csomók számát

c

-vel. ²
Az

a

oldalú négyzetben

K

számú ötszög teljesen benne van, ezért legalább

K \cdot k_{1}

számú olyan csúcs van, amelynek csomójából

e_{1}

él indul ki. Így

K \cdot k_{1}

nem lehet nagyobb, mint a négyzetben lévő

e_{1}

élű csomókban összeeső csúcsok száma; vagyis

K \cdot k_{1} \leq e_{1} \cdot c_{1}

. Ennélfogva:

\begin{matrix} \frac{K}{e_{1}} \leq \frac{c_{1}}{k_{1}} . \end{matrix}

Hasonló egyenlőtlenségeket kapunk

e_{2}

e_{3}

e_{4}

e_{5}

-re; ezeket összeadva:

\begin{matrix} \frac{K}{e_{1}} + \frac{K}{e_{2}} + \frac{K}{e_{3}} + \frac{K}{e_{4}} + \frac{K}{e_{5}} = K (\frac{1}{e_{1}} + \frac{1}{e_{2}} + \frac{1}{e_{3}} + \frac{1}{e_{4}} + \frac{1}{e_{5}}) \leq \\ \leq \frac{c_{1}}{k_{1}} + \frac{c_{2}}{k_{2}} + \frac{c_{3}}{k_{3}} + \frac{c_{4}}{k_{4}} + \frac{c_{5}}{k_{5}} . \end{matrix}

Itt a jobb oldalon

k_{i}

számú olyan tört áll, melynek nevezője

k_{i}

, ezek számlálója a fentiek szerint azonos, így összegük

c_{i}

, és a jobb oldal értéke éppen¹

c

, eszerint

\begin{matrix} \frac{1}{e_{1}} + \frac{1}{e_{2}} + \frac{1}{e_{3}} + \frac{1}{e_{4}} + \frac{1}{e_{5}} = E \end{matrix}

A nyert egyenlőtlenségből az 1. közleményben bebizonyított

\begin{matrix} K > \frac{{(a - 2 d)}^{2}}{t} \end{matrix}

(2)

egyenlőtlenség figyelembevételével

\begin{matrix} \frac{{(a - 2 d)}^{2}}{t} \cdot E < c . \end{matrix}

(5)

(Természetesen ismét eleve feltesszük, hogy

a

lényegesen nagyobb

d

-nél, mindenesetre

a > 2 d

.)
Meggondolásunkat az

a

oldalú négyzetben levő és oda benyúló

L

számú sokszögre ismételve

K

helyére mindenütt

L

lép, és az egyenlőtlenségek iránya ellentétes a fentiekkel, mert ez az

L

számú sokszög lefedi az

a

oldalú négyzetet. Ennélfogva a korábban megállapított

\begin{matrix} L < \frac{{(a + 2 d)}^{2}}{t} \end{matrix}

(1)

becslést is figyelembe véve

\begin{matrix} L \cdot E \geq c és \frac{{(a + 2 d)}^{2}}{t} \cdot E > c . \end{matrix}

(6)

A lefedés minden csomójában

360^{\circ}

szögtér van. Ahogyan az V. tétel bizonyításában (4)-ben alulról becsültük meg a csomókban levő szögek összegét, hasonlóan itt alulról és felülről becsülve a következő egyenlőtlenséget kapjuk:

\begin{matrix} K \cdot 540^{\circ} \leq c \cdot 360^{\circ} \leq L \cdot 540^{\circ}, \end{matrix}

azaz osztással, valamint (1) és (2) figyelembevételével

\begin{matrix} \frac{{(a - 2 d)}^{2}}{t} \cdot \frac{3}{2} < c < \frac{{(a + 2 d)}^{2}}{t} \cdot \frac{3}{2} . \end{matrix}

(7)

Megmutatjuk, hogy a fenti

E

szám értéke

3 / 2

, mégpedig úgy, hogy az

E : 3 / 2 = q^{2}

hányados értéke 1-gyel egyenlő. (5) és (7) összetevéséből kapjuk:

\begin{matrix} \frac{{(a - 2 d)}^{2}}{t} \cdot E < \frac{{(a + 2 d)}^{2}}{t} \cdot \frac{3}{2}, \end{matrix}

(8)

(6) és (7) összetevéséből pedig:

\begin{matrix} \frac{{(a + 2 d)}^{2}}{t} \cdot E > \frac{{(a - 2 d)}^{2}}{t} \cdot \frac{3}{2} . \end{matrix}

(9)

Eszerint (9)-ből és (8)-ból (

q

-val

q^{2}

pozitív négyzetgyökét jelölve)

\begin{matrix} \frac{a - 2 d}{a + 2 d} < q, és \frac{a + 2 d}{a - 2 d} > q, \end{matrix}

azaz

\begin{matrix} (1 - q) \cdot a < (1 + q) 2 d, (q - 1) \cdot a < (1 + q) \cdot 2 d . \end{matrix}

Csak akkor teljesülhet mind a két egyenlőtlenség tetszés szerinti nagy

a

-ra, ha

1 - q = 0

q = 1

. Így valóban

q^{2} = 1

, tehát

E = 3 / 2

, és így az

e_{i}

, számokra

\begin{matrix} \frac{1}{e_{1}} + \frac{1}{e_{2}} + \frac{1}{e_{3}} + \frac{1}{e_{4}} + \frac{1}{e_{5}} = \frac{3}{2} . \end{matrix}

(10)

Válasszuk már most az indexeket úgy, hogy álljon

e_{1} \leq e_{2} \leq e_{3} \leq e_{4} \leq e_{5}

. Így

\begin{matrix} \frac{1}{e_{1}} \geq \frac{1}{e_{2}} \geq \frac{1}{e_{3}} \geq \frac{1}{e_{4}} \geq \frac{1}{e_{5}}, tehát \\ 5 \cdot \frac{1}{e_{1}} \geq E = \frac{3}{2}, és így e_{1} \leq \frac{10}{3} < 4. \end{matrix}

Másrészt minden csomópontból legalább

3

él indul ki:

e_{1} \geq 3

, ezekből következik, hogy

e_{1} = 3

. ‐ Hasonlóan

\frac{4}{e_{2}} \geq E - \frac{1}{3} = \frac{7}{6}

, vagyis

e_{2} \leq \frac{24}{7} < 4

, tehát

e_{2} = 3

, folytatólag

e_{3} \leq \frac{15}{8} < 4

, tehát

e_{3} = 3

, majd ugyanígy

e_{4} \leq 4

. Eszerint, mivel

e_{4}

megválasztásával (10)-ből

e_{5}

értéke is határozottá válik, két esetet kell tekintenünk:

\begin{matrix} a) ha e_{4} = 3, akkor e_{5} = 6, \\ b) ha e_{4} = 4, akkor e_{5} = 4 \end{matrix}

(mindkétszer teljesül

e_{5} \geq e_{4}

).
Azt kaptuk, hogy ha egyáltalán van egyenletes ötszögparkettázs, abban egy-egy ötszög csúcsai a háromélű csomók mellett vagy egy 6-élű, vagy két 4-élű csomóba illeszkednek. E két esetet külön-külön vizsgáljuk tovább.
a) eset. Az ötszögek szögeinek és oldalainak nagyságától ideiglenesen eltekintünk, csak azt vizsgáljuk, hogy ha egyáltalán van olyan egyenletes lefedés, melynek 6-élű csomói is vannak, akkor milyen a lefedés váza, és a vázban mely csúcsok felelnek meg egymásnak.
Tekintsünk egy hatélű csomót, jelöljük

R_{0}

-lal (14. ábra).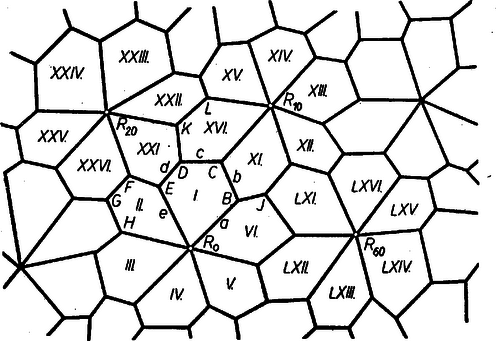

14. ábra

Az ide befutó

I - V I

ötszögek többi csúcsai (pl.

B

C

D

) a lefedésnek háromélű csomói. Az így kapott tizennyolcszög minden harmadik csúcsába már

3

él fut be (pl.

B

E

H

), ezekből már nem indulhat ki több él, a többi csúcsba pedig (pl.

C

D

F

G

) az eddig megrajzolt ötszögeknek 2‐2 éle fut be, s így ezekből a meglevőkön kívül még

1

‐

1

él indul ki.
Az

I

és

V I

ötszögek közös

3

-élű

B

csomópontjába befutó harmadik ötszög legyen

X I

. Mivel

X I

-nek már három csúcsa megvan (

J

B

és

C

), s ezek

I

és

V I

-ból háromélű csomók,

X I

egyetlen hatélű csomóját vagy

J

-vel, vagy

C

-vel él köti össze. Feltehetjük, hogy a

X I

-re illeszkedő hatélű

R_{10}

csomót

C

-vel köti össze egy él (

C R_{10}

X I

ötszög oldala).
Az

R_{10}

csomóba befutó

X I - X V I

ötszögek hatélű csomója

R_{10}

, ezért ezen ötszögek további csúcsai háromélű csomókra illeszkednek.
Az

R_{0}

és

R_{10}

csomókból kiinduló élek másik végpontjára (pl.

B

E

H

;

C

L

), valamint az

I

és

X V I

ötszögek közös

D

és a

V I

és

X I

ötszögek közös

J

csúcsára csak a meglévő élek illeszkednek, az eddig lefedett terület határán levő többi csúcsokban pedig egy-egy újabb él végződik. Ennélfogva a

I I

I

és

X V I

ötszögeknek van egy közös szomszédjuk, legyen ez

X X I

X X I

-nek négy csúcsa:

F

E

D

és

K

már adott, ezek háromélű csomókban vannak, ezért ötödik csúcsa egy

R_{20}

hatélű csomóra illeszkedik.
Hasonlóképpen a

V I

X I

, és

X I I

ötszögeknek is van egy

L X I

közös szomszédja. Ezen ötszögnek is négy csúcsa adott; ezek a lefedésben háromélű csomók, ezért az ötödik csúcs egy

R_{60}

hatélű csomóba esik. Ennélfogva az

R_{20}

és

R_{60}

hatélű csomókba befutó

X X I - X X V I

és

L X I - L X V I

ötszögek váza egyértelműen megrajzolható.
A váz felépítését ehhez hasonlóan, egyértelmű lépések sorozatával folytathatjuk. Látható, hogy az

I - V I

ötszögek egységét hat ugyanilyen egység teljesen körülveszi. A továbbiakban az ilyen egységeket (egy hatélű csomóra illeszkedő hat ötszög) rózsáknak nevezzük, s a hatélű csomójának betűjével utalunk rá, pl. az

I - V I

ötszögek alkotta rózsát

R_{0}

-nak nevezzük.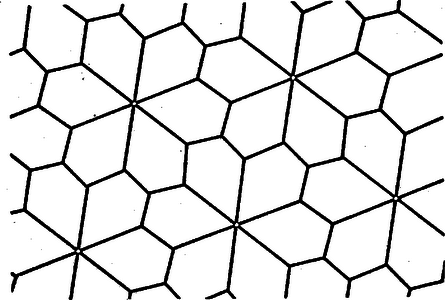

15. ábra

Kimutatjuk, hogy ‐ ha egyáltalán van ilyen vázú lefedés, akkor ‐ egy rózsa ötszögeit a rózsa hatélű csomója körüli forgatással egymásba vihetjük át. Ehhez elegendő bizonyítanunk, hogy pl. az

I

ötszöget forgatással átvihetjük a

I I

ötszögbe.
A definíció szerint van olyan transzformáció, mely

I

-et úgy viszi át

V I

-ba, hogy az eredeti és transzformált parkettázs élei megegyezzenek. Mivel az

R_{0}

pont csakis önmagába mehet át, ez a transzformáció vagy az

R_{0} E

tengelyre való tükrözés, vagy az

R_{0}

csomópont körüli forgatás. Kimutatjuk, hogy az előbbi lehetetlen. Ha ugyanis

I

tengelyes tükrözéssel menne át

I I

-be,

R_{0}

és

E

helyben maradása miatt

D

F

pontba menne át. Ez viszont lehetetlen, mert az eredeti parkettázsban a

D

-re illeszkedő élek háromélű csomókba futnak, az

F

-re illeszkedő élek végpontjai közül viszont

R_{20}

hatélű. Ennélfogva egy rózsán belül az ötszögeket a rózsa hatélű csomója körüli forgatással egymásba vihetjük át, vagyis bármely rózsa hat ötszögében a megfelelő csúcsok azonos körüljárás szerint következnek egymás után.
Bebizonyítjuk, hogy különböző rózsák ötszögei is azonos körüljárásúak. Ehhez elegendő kimutatnunk, hogy két szomszédos rózsa, pl. az

R_{10}

és

R_{20}

rózsa ötszögeinek körüljárási iránya ugyanaz. Fent beláttuk, hogy az

I

ötszöget csak az

R_{0}

csomó körüli forgatás viheti át

I I

-be úgy, hogy az eredeti és transzformált parkettázs vázai megegyezzenek. Ez a forgatás az

R_{10}

csomót az

R_{20}

csomóba, az

R_{10}

rózsa ötszögeit az

R_{20}

rózsa ötszögeibe viszi. Mivel a forgatás nem változtatja meg a sokszög körüljárási irányát, az

R_{10}

és

R_{20}

rózsa ötszögei ugyanolyan körüljárásúak. Hasonlóan látható be, hogy az

R_{20}

és

R_{0}

R_{10}

és

R_{0}

R_{0}

és

R_{60}

rózsa ötszögeinek körüljárási iránya ugyanaz. Mivel bármely rózsából kiindulva eljuthatunk a parkettázs bármely rózsájához úgy, hogy mindig szomszédos rózsára lépünk át, a fentiekből valóban következik, hogy a parkettázs bármely két ötszöge ugyanolyan körüljárású.
Betűzzük meg az

I

öszög oldalait a következőképpen:

R_{0} B = a

B C = b

C D = c

D E = d

E R_{0} = e

, s az

R_{0}

B

C

D

E

csúcsokban levő szöget jelöljük rendre

α

β

γ

δ

ε

-nal. Ekkor a

I I

I I I

I V

V

V I

ötszögek

R_{0}

csúcsában levő szög is

α

nagyságú, ezért

α = \frac{360^{\circ}}{6} = 60^{\circ}

. Az ötszögek körüljárási irányának azonossága miatt a

I I

ötszögben

R_{0} E = a

E F = b

, az

E

-nél levő szög

β

; a

X X I

ötszögben

F E = b

E D = c

D K = d

, az

E

-nél levő szög

γ

, a

D

-nél levő szög

δ

; a

X V I

ötszögben pedig

K D = c

D C = d

, és a

D

-nél levő szög

δ

. Ennélfogva

R_{0} E = a = e

C D = c = d

(ugyanígy:

D E = d = c

). A csomópontokban levő szögek összege

360^{\circ}

, ezért az

E

csomópont alapján:

\begin{matrix} ε + γ + β = 360^{\circ} \end{matrix}

D

csomópontban összefutó szögekre pedig:

\begin{matrix} δ + δ + δ = 3 δ = 360^{\circ}, \end{matrix}

s így

\begin{matrix} δ = 120^{\circ} . \end{matrix}

A lefedésnek a 15. ábrán bemutatott részletéből láthatjuk, hogy a fent kimondott feltételeknek eleget tevő ötszöggel (16. ábra) valóban készíthető lefedés.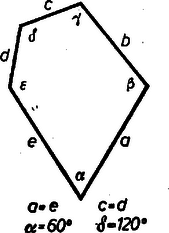

16. ábra

Ez egyben annak is bizonyítása, hogy a) esethez valóban tartozik ötszögparkettázs.
b) eset. Az egyenletes parkettázs feltételeinek eleget tevő ötszögeket ebben az esetben is a lefedés vázából kiindulva határozhatjuk meg. Itt kétféle váz lehetséges, mert egy ötszög négyélű csomóba illeszkedő csúcsait vagy oldal köti össze, vagy nincsenek összekötve. E két váz kiépítése, majd az adódó diszkussziók elvégzése után a következő eredményt kapnók:
Jelöljük a parkettázs ötszögének oldalait és szögeit rendre

a

b

c

d

e

, ill.

α

β

γ

δ

ε

-nal (ahol

a

és

b

szöge

β

b

és

c

szöge

γ

). Ha a parkettázs egy ötszögének négyélű csomóba illeszkedő csúcsait az

e

oldal köti össze, akkor (17. ábra)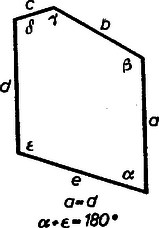

\begin{matrix} a = d \end{matrix}

17. ábra

Ha a négyélű csomókat nem köti össze él, akkor a következő összefüggéseknek kell fennállniuk:
vagy

a = d

c = e

és

α + δ 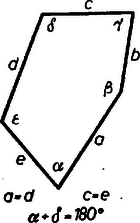= 180^{\circ}

(18. ábra),

18. ábra

vagy

a = e

c = d

és

α = δ 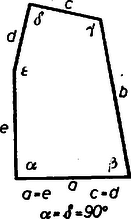= 90^{\circ}

(19. ábra).

19. ábra

A 20., 21. és 22. ábrán látható parkettázsrészletek bemutatják, hogy ezen ötszögekkel milyen rendszer szerint fedhetjük le a síkot.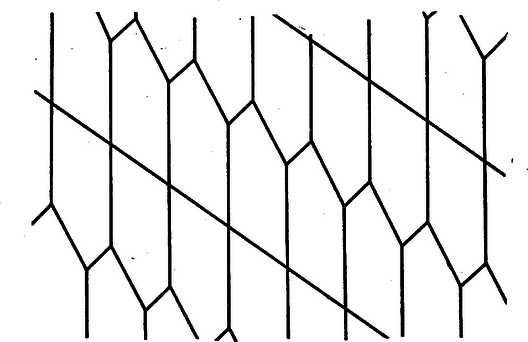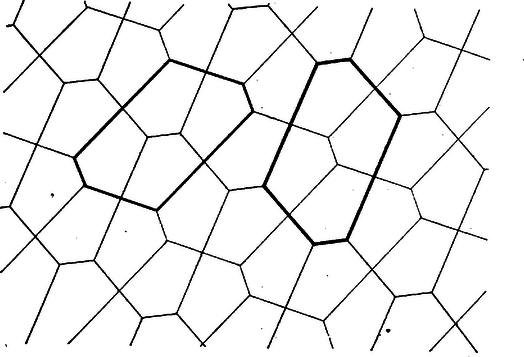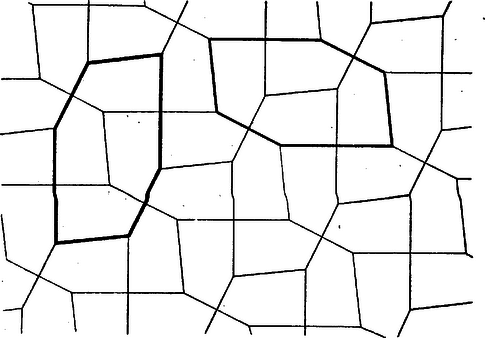

20. ábra

21. ábra

22. ábra

Megállapításainkat a következő tételben foglalhatjuk össze:
VI. tétel: Egy ötszögből akkor és csak akkor készíthető egyenletes lefedés, ha az ötszögben megvannak a 16., 17., 18. és 19. ábra ötszöge közül legalább egynek a tulajdonságai.
Megjegyzendő, hogy az ismert ötszögparkettázsok nem mind egyenletesek.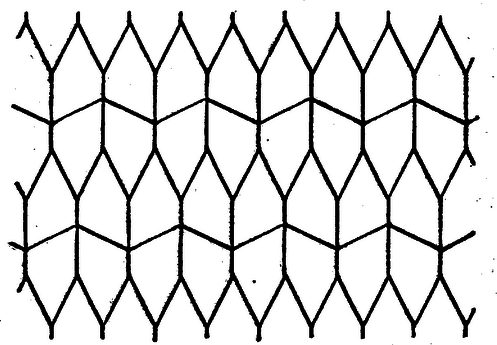

23. ábra

A 23. ábrán látható másodfajú ötszögparkettázs pl. nem egyenletes, és alapötszögével nem is lehet egyenletes parkettázst készíteni. (Ezen ötszögre a

b = c

β = δ

és

α + ε = 180^{\circ}

összefüggések állnak.)
A konvex sokszögekkel történő lefedéshez hasonlóan igen érdekes problémák adódnak a konkáv sokszögekből képezhető parkettázsok körében is. Ott a problémák még szerteágazóbbak, még több megoldatlan kérdést ismerünk. Sok esetben a konvex parkettázsokkal ellenkező, néha viszont megegyező tételek állanak fenn. Könnyen belátható pl. hogy az V. tételnek éppen az ellenkezője érvényes: bármely

n > 3

-ra megadható konkáv

n

-szög, amellyel parkettázs készíthető.

(Ilyet ad

n = 5

-re a 7. ábra konkáv centrálszimmetrikus hatszögének olyan a centrumon átmenő egyenes kettévágása, amely nem megy át csúcson; ilyenek

n = 18

-ra a 14. ábra rózsái,

n = 9

-re ugyanott a

V I

X I

L X I

idomok együttese,

n = 42

-re ugyanott az

R_{0}

R_{10}

R_{20}

R_{60}

rózsák együttese.) Említettük viszont, hogy a II. tétel konkáv négyszögekre is érvényes.

¹Ha pl.

e_{1} = e_{3} = e_{4} \neq e_{2} = e_{5}

, akkor

k_{1} = k_{3} = k_{4} = 3

, és

k_{2} = k_{5} = 2

²Avégett, hogy e jelölések tartalmát világosan lássuk, gondoljuk át a következőket. Ha $k_{i} > 1$ , vagyis az ötszögnek nem csak az $i$ -edik csúcsából indul ki $e_{i}$ számú él, és pl. a $j$ -edik csúcs is ilyen: $e_{j} = e_{i}$ , akkor $c_{i}$ és $c_{j}$ ugyanazt a számot jelölik más alakban; az előző lábjegyzet példájában egyrészt $c_{1} = c_{3} = c_{4}$ , másrészt $c_{2} = c_{5}$ , és így $c = c_{1} + c_{2}$ . (Tehát $c_{1} + c_{2} + c_{3} + c_{4} + c_{5} > c .$ ) ‐ Ha viszont $k_{j} = 1$ , vagyis $e_{i}$ minden más $e_{j}$ -től különböző szám, akkor az illető csomóban levő csúcsok az ötszögek egymásnak megfelelő csúcsai, ezért az itt levő szögek egyenlők, közös értékük $360^{\circ} / e_{i}$ .

¹Az előbbi példában
$\frac{c_{1}}{k_{1}} = \frac{c_{3}}{k_{3}} = \frac{c_{4}}{k_{4}} = \frac{c_{1}}{3}$ és $\frac{c_{2}}{k_{2}} = \frac{c_{5}}{k_{5}} = \frac{c_{2}}{2}$ ; ennélfogva a jobb oldal $3 \cdot \frac{c_{1}}{3} + 2 \cdot \frac{c_{2}}{2} = c_{1} + c_{2} = c$ .