Cím: A sík lefedése egybevágó konvex sokszögekkel 1.
Szerző(k):  Bollobás Béla 
Füzet: 1961/február, 49 - 56. oldal  PDF  |  MathML 
Témakör(ök): Szakmai cikkek

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

A sík lefedése egybevágó konvex sokszögekkel1

(1. közlemény)

 

1. Az elemi geometriának érdekes kérdéscsoportját alkotják az ún. lefedési feladatok. Bár egyrészük igen egyszerű eszközökkel tárgyalható, mégis számos nehéz és még megoldatlan probléma tartozik ebbe a körbe.
Síkidomok valamely rendszere egyrétűen és hézagtalanul fedi le a síkot, ha a sík minden pontja valamely síkidom belsejében vagy a határán van, és nincs a síkon olyan pont, amely benne lenne két síkidom belsejében is. Azt mondhatjuk, hogy a lefedő idomok nem nyúlhatnak egymásba, úgy helyezkednek el, mint a padlózat parkettái; ezért a sík egyrétű lefedését parkettázsnak is szokás nevezni.
A továbbiakban a sík olyan egyrétű és hézagtalan lefedéseivel foglalkozunk, amelyekben a fedőidomok egybevágó konvex sokszögek ‐ tehát eltolással, forgatással, tükrözéssel egymásba átvihetők ‐, lefedésen (parkettázson) a következőkben ilyen lefedést értünk. Néhol utalunk majd arra, hogy állításaink konkáv (de nem hurkolt) fedőidomokra is érvényesek. Ha a sík egy adott konvex sokszöggel egybevágó sokszögeket felhasználva lefedhető, azt mondjuk, hogy a sokszögből lefedés (parkettázs) készíthető, vagy a sík a sokszöggel lefedhető.
Nem minden sokszögből készíthető parkettázs. Közismert pl., hogy a szabályos sokszögek közül csak a három-, négy- és hatszögből készíthető parkettázs, de nem készíthető pl. öt-, hét- és nyolc oldalúból, mert olyan és csak olyan szabályos sokszögből készíthető, melyben egy szög valamely többszöröse 360∘.
Másrészt, ha valamely sokszögből képezhető parkettázs, akkor a lerakás ‐ az idomok egymás mellé illesztése ‐ általában nem tetszés szerinti. Nyilvánvaló pl., hogy a szabályos hatszög egy példányát letéve, az ehhez kapcsolódó 6 hatszög helyzete és folytatólag a lefedés minden hatszögének helyzete egyértelműen meghatározott. Hasonlóképpen egyértelműen meghatározott az idomok csatlakozása a 6. ábrán. Viszont pl. szabályos háromszöggel, melynek magassága m, le lehet fedni a sík olyan végtelen szalagját, melyet két egymástól m távolságban haladó párhuzamos határol; ilyen szalagokat egymás mellé illesztve az egész sík lefedhető, de a szalagok egymás mellett tetszés szerint elcsúsztathatók (1. ábra, ilyenféle az ún. hajópadló és a téglakötés is ‐ 2. ábra ‐, a padlóburkolat, a fal így erősebb).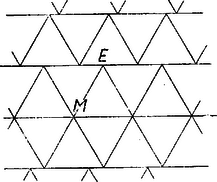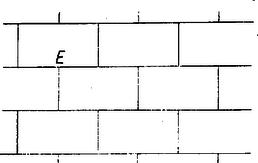
 
 
1. ábra
 

 
 
2. ábra
 

Ezek szerint a lefedő idom alakja mellett a lerakási módot is tekintetbe kell vennünk.
Állapodjunk meg néhány elnevezésben, melyeket gyakran használunk. A sík azon pontjait, melyekben a fedőidomoknak csúcsai vannak, csomópontoknak, röviden csomóknak nevezzük. Egy csomóban tehát több csúcs van, legalább kettő. Azokat a szakaszokat, melyekben a fedőidomoknak oldalai vannak, továbbá melyeknek végpontjai csomópontok és belsejükben nincs csomópont, éleknek nevezzük. A csomót másodfajúnak nevezzük, ha minden rajta átmenő oldalnak végpontja (1. ábra, M), és elsőfajúnak, ha valamely oldalnak belső pontja (1. és 2. ábra, E). Látható, hogy minden elsőfajú csomóban legalább 2, minden másodfajúban legalább 3 csúcs esik egybe. Az egy csomót alkotó csúcsoknál levő szögek összege elsőfajú csomóban 180∘, másodfajúban 360∘. ‐ Ha a lefedés minden csomója másodfajú, vagyis egy csúcs sem esik egy másik sokszög oldalának belsejébe, a lefedést másodfajúnak nevezzük. ‐ Beszélünk majd a parkettázs vázáról is, ezen az élek és csomók olyan rendszerét értjük, melyben hosszúságokra, szögek nagyságára nem vagyunk tekintettel. A váz csak azt határozza meg, hogy egy-egy csomóból hány él indul ki, és hogy mely csomók vannak élekkel összekötve.
2. Felvetődik a kérdés: milyenek azok a konvex sokszögek, amelyekből parkettázs készíthető? A sokszög oldalainak száma tekintetében a probléma meg van oldva: lefedés csak 3-, 4-, 5- és 6-szögből építhető ki. A sokszög alaki tulajdonságaira azonban 5- és 6-szögek esetében még csak részeredmények vannak. Alább elsősorban ezekre a kérdésekre vonatkozó eredményeket mutatunk be, a lerakás kérdését csak mellékesen érintjük. Előkészítésül két egyszerű lefedést mutatunk be.
Mindenki ismeri a paralelogramma rácsot, ez paralelogrammából készített parkettázsnak tekinthető (3. ábra).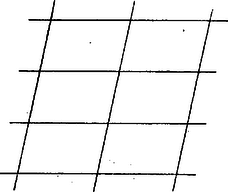
 
 
3. ábra
 

Ilyet bármely paralelogrammából készíthetünk. (A rácsban elsősorban a rácspontokat szokás tekinteni, ezért bármely rácshoz végtelen sok paralelogramma parkettázs tartozik.) A 4. és 5. ábrák két további példát mutatnak arra, hogy a parkettázst az alapparalelogramma nem határozza meg egyértelműen.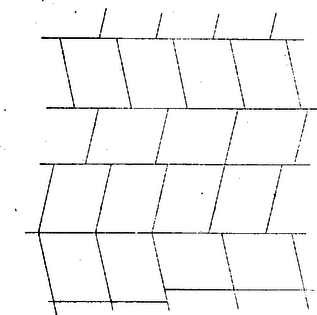
 
 
4. ábra
 

Az 5. ábra példáján a paralelogramma oldalainak aránya racionális szám, ilyen esetekben több, egymásba eltolással át nem vihető paralelogrammából nagyobb paralelogrammákat építhetünk ki.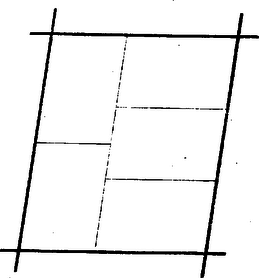
 
 
5. ábra
 

Kevésbé ismert, de szintén igen egyszerű lefedést készíthetünk bármely (konvex vagy konkáv) centrálisan szimmetrikus hatszögből (6. és 7. ábra). Vegyünk egy centrálszimmetrikus hatszöget és toljuk el úgy, hogy egyik oldala a szemközti oldallal essék egybe. Az eltolást ugyanígy folytatva ‐ mindig ugyanazok az oldalpárok essenek egybe ‐ végtelen sok hatszögből álló, fogazott szélű szalagot kapunk.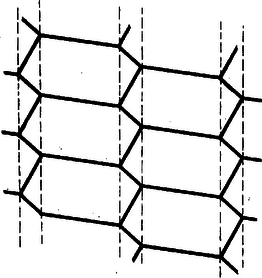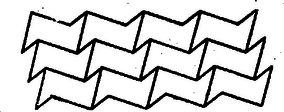
 
 
6. ábra
 

 
 
7. ábra
 

Mivel két ilyen szalag újabb alkalmas (más irányú) eltolással hézagtalanul összeilleszthető, azért akárhány bármilyen hosszú ilyen szalagot egymáshoz illeszthetünk, s így az egész síkot lefedhetjük.
Ezek alapján könnyen választ adhatunk arra a kérdésre, hogy a sík milyen háromszögekkel és négyszögekkel fedhető le.
I. tétel: A sík bármely háromszöggel lefedhető.
Egy tetszés szerinti háromszöget bármelyik oldalának felezőpontjára tükrözve paralelogrammát kapunk. A sík ezzel a paralelogrammával lefedhető. A lefedés paralelogrammáit az eredeti háromszöggel egybevágó háromszögekre bonthatjuk, ezért a sík lefedhető az eredeti háromszöggel.
II. tétel: A sík bármely (konvex vagy konkáv) négyszöggel lefedhető.
Az előzőhöz hasonlóan bármely négyszöget egyik oldalának felezőpontjára tükrözve vagy centrálszimmetrikus hatszöget, vagy paralelogrammát kapunk (8. ábra), ebből pedig készíthető parkettázs.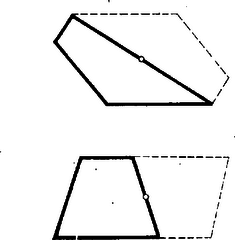
 
 
8. ábra
 

(Konkáv négyszögnek csak egy 180∘-nál nagyobb szöge lehet, így a tükrözés ilyen szög melletti oldal felezőpontján is lehetséges. Konvex négyszögből kiindulva konkáv hatszöghöz is juthatunk.)
Az ötszög parkettázsokra vonatkozó alábbi eredmények részben elégséges, részben szükséges feltételt adnak a lefedésre alkalmas ötszögre. Olyan feltétel, amely szükséges is, elégséges is, eddig nem ismeretes.
IIIa. tétel: A sík bármely olyan ötszöggel lefedhető, melyben két szomszédos szög összege 180∘.
A szóban forgó szögek nem közös szárai párhuzamosak, így az ötszöget a csúcsaik közti oldal felezőpontjára tükrözve centrálszimmetrikus hatszöget kapunk (9. ábra).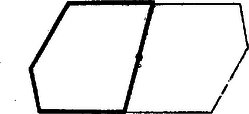
 
 
9. ábra
 

IIIb. tétel: Ha valamely ötszögből parkettázs készíthető, akkor nem lehet az ötszög minden szöge tompaszög.
Tegyük fel, hogy egy ötszögnek minden szöge tompaszög, és mégis készíthető belőle parkettázs. Így a lefedés minden csomója másodfajú, mert két tompaszög összege nagyobb az elsőfajú csomók 180∘-os szög terénél. Ennélfogva minden csomóból pontosan három él indul ki, mert az ötszög bármelyik négy szögének összege nagyobb és bármelyik két szögének összege kisebb 360∘-nál, a másodfajú csomók szögterénél.
Ezek alapján egy ötszögből kiindulva egyértelműen megkezdhetjük a parkettázs vázának kiépítését (10. ábra).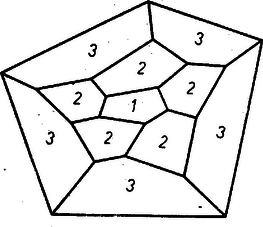
 
 
10. ábra
 

Az 1-es ötszögre támaszkodó öt 2-es ötszög szükségképpen páronként egymáshoz is támaszkodik; így 3‐3 oldalak már foglalt, szabad oldalaik együttes száma 10, az ezeken levő csomók váltakozva máris 2-, ill. még csak 2-élűek. Így az öt 3-élű csomóba befutó, 3-as ötszögek az eddigiekhez két oldalukkal, egymáshoz pedig az öt, eddig 2-élű csomóból kiinduló harmadik élekben egy-egy oldalukkal támaszkodnak, tehát 4 oldaluk foglalt, szabad oldalaik együttes száma 5. Ezek olyan ötszöget alkotnak, melynek minden csomójában már most 3 él fut össze. Eszerint a felépítés nem folytatható, a feltevés helytelen volt. Tehát ha az ötszögből parkettázs építhető ki, akkor van legalább egy 90∘-nál nem nagyobb szöge.
Megvizsgálva, hogy a bizonyításban mit használtunk fel, rájövünk, hogy lényegesen általánosabb tételt bizonyítottunk be: a síkot nem lehet ötszögekkel úgy lefedni, hogy minden csomóból pontosan három él induljon ki, még akkor sem, ha nem követeljük az ötszögek egybevágóságát.
IIIc. tétel: Ha valamely ötszögből másodfajú parkettázs építhető ki, akkor az ötszögnek van két egyenlő oldala.2
Tegyük fel az állítással ellentétben, hogy van csupa különböző oldalú ötszög, amelyből másodfajú parkettázs készíthető. Így az ötszögek csak a megfelelő oldalaik mentén illeszkedhetnek egymáshoz. Könnyű belátnunk, hogy az ebből kiépített parkettázs minden csomójából legalább négy él indul ki. Ha ugyanis lenne egy 3-élű csomója, amelyben az I, II, III ötszögek páronként az a, b, c hosszúságú éleikkel illeszkednének (11. ábra), akkor az I és II ötszögből adódik, hogy a-nak b és c szomszédai, így b és c az I és II ötszögben második szomszédok, mivel nincs az ötszögnek még egy a hosszúságú oldala; viszont b és c a III ötszögben szomszédosak.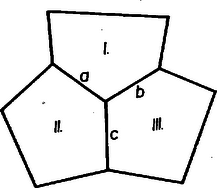
 
 
11. ábra
 

Ellentmondásra jutottunk, így a lefedésnek egy csúcsa sem lehet 3-élű, minden csúcs legalább 4-élű.
Tekintsük a parkettázs egyik P ötszögét az őt körülvevő ötszögekkel együtt (12. ábra).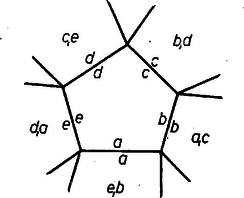
 
 
12. ábra
 

Jelöljük P egymás utáni oldalait a, b, c, d, e-vel. Mivel ezek különbözők, és a parkettázs másodfajú, azért a Pa-oldalához illeszkedő ötszögnek a közös a oldal végpontjaiból mint csomókból kiinduló további élei közül az egyik b, a másik e hosszúságú. Hasonlóan a b oldal végpontjaiból egy-egy további a és c, a c oldal végpontjaiból egy-egy b és d, a d oldal végpontjaiból egy-egy c és e, végül e végpontjaiból egy-egy d és a hosszúságú él indul ki ‐ esetleg további más élek mellett. Vagyis a P összes csúcsaiba mint csomókba befutó élek között mindegyik ötszögél legalább további kétszer szerepel. Másrészt mindegyik csomóból legalább 4 él indul ki, azért az ötszög oldalaihoz támaszkodó ötszögek közé minden egyes csúcsban benyúlik még legalább egy további ötszögnek egy szöge. Ez az öt ‐ vagy több ‐ benyúló szög a bezáró oldalak hossza szerint legalább háromféle (nagyságra természetesen lehetnek egyenlők is), mert ha csak kétféle szög szerepelne, akkor legfeljebb négy különböző él alkotná őket, ennélfogva száraik között nem szerepelhetne mind az öt oldal. Legyen az ötszög három olyan szöge, amely szerepel a benyúló szögek között, α, β, γ. A P öt csúcsánál mint csomóknál levő szögek összege 5⋅360∘=1800∘. Ez összetevődik egyrészt P belső szögeiből (540∘), ezenkívül az oldalakhoz támaszkodó ötszögek szögeiből ‐ amelyek között az ötszög mindegyik szöge kétszer szerepel, és így összegük 2⋅540∘ ‐ végül a benyúló szögekből. Ha a benyúló szögek közül α, β, γ mindegyikét csak egyszer vesszük figyelembe, akkor nyilvánvaló, hogy
1800∘>540∘+2⋅540∘+α+β+γ,
azaz
α+β+γ<180∘.
Így pedig az ötszög további két szögének összege nagyobb 360∘-nál, tehát legalább egyikük nagyobb 180∘-nál, az ötszög nem konvex. Ellentmondásra jutottunk, feltevésünk nem állhat fenn, vagyis az ötszögnek van két egyenlő oldala. Ezt akartuk bizonyítani.
Megjegyezzük, hegy itt a végtelenbe nyúló parkettázs létezését sem használtuk ki, csak az egy ötszöghöz éllel vagy csúccsal csatlakozó ötszögeket vettük tekintetbe. ‐ A bizonyítás első részében azt sem használtuk ki, hogy ötszögről van szó, csak három különböző oldalról beszéltünk. Így ha egy tetszőleges másodfajú parkettázs alapsokszögének ‐ ami legalább háromszög ‐ nincs két egyenlő oldala, akkor minden csomópontjából legalább négy él indul ki.
Hasonlóan látható be a következő állítás:
IV. tétel: Ha valamely hatszögből kiépíthető másodfajú parkettázs, akkor a hatszögnek van két egyenlő oldala. ‐
Bebizonyítjuk, hogy a lefedő sokszög oldalainak száma tovább nem emelhető.
V. tétel: Hatnál nagyobb oldalszámú konvex sokszöggel nem készíthető parkettázs.
Feltesszük, hogy van olyan konvex n-szög (n≥7), amellyel a sík lefedhető. Legyen az n-szög területe t és egy tetszés szerinti, a sokszöget fedő kör átmérője d. (E kört végtelen sokféleképpen választhatjuk, de egyszeri megválasztása után nem változtatjuk.) Eszerint a sokszög bármely két pontjának távolsága nem nagyobb d-nél, hiszen d-nél hosszabb szakaszt nem lehet d átmérőjű körrel lefedni. Be fogjuk látni, hogy nem fedhető le akármilyen nagy négyzet az n-szöggel. Ezt az eredményt egy nagy négyzetben levő sokszögek és csomópontok számának különböző módokon való megbecslésével fogjuk nyerni.
Borítsunk a lefedettnek gondolt síkra egy a oldalú négyzetet. Jelöljük a négyzetben levő első-, ill. másodfajú csomópontok számát s1, ill. s2-vel, a négyzetben teljesen benne levő sokszögek számát K-val, a bennlevő és benyúló sokszögek együttes számát L-lel (egy sokszöget akkor mondunk benyúlónak, ha belső pontja is van a négyzetben).
Húzzunk az a oldalú négyzet oldalaitól d távolságra párhuzamosokat. A négyzeten kívül haladó párhuzamosok egy a+2d oldalú négyzetet határoznak meg, amely magába foglalja az a oldalú négyzetet, a többi párhuzamosok pedig egy a-2d oldalú négyzetet, ez benne van az a oldalúban (13. ábra).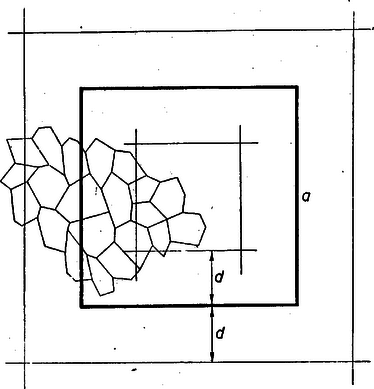
 
 
13. ábra
 

A t, d, a értékek alapján becslést adhatunk a K és L számokra. Az a oldalú négyzet belsejében levő és az abba benyúló sokszögek benne vannak az a+2d oldalú négyzetben. Más szóval az a+2d oldalú négyzet lefedi az a oldalú négyzetben levő és oda benyúló sokszögeket, ezért az L számú sokszög területe kisebb az a+2d oldalú négyzet területénél (még akkor is áll ez, ha L-be tartoznak a csak csúcsukkal az a oldalú négyzethez érő sokszögek is), azaz
L⋅t<(a+2d)2,vagyisL<(a+2d)2t.(1)


Hasonlóan az a oldalú négyzetben levő sokszögek lefedik az a-2d oldalú négyzetet, ezért a K számú sokszög együttes területe nagyobb az a-2d oldalú négyzet területénél, és ebből
K>(a-2d)2t.(2)

(1) és (2) alapján felső és alsó becslést adhatunk az s1 és s2 számokra, ugyancsak t, d, és a, valamint n felhasználásával. Az a oldalú négyzet belső csomópontjaiba csak olyan sokszögek csúcsai eshetnek, amelyek vagy az a oldalú négyzetben vannak, vagy oda benyúlnak. E csomópontokba eső csúcsok száma tehát nem nagyobb az L számú sokszög összes csúcsainak számánál, ami L⋅n. Mivel az elsőfajú csomókba legalább két, a másodfajúakba legalább három csúcs esik, azért
2s1+3s2≤L⋅n.
Másrészt (1) alapján
L⋅n<(a+2d)2t⋅n,
ezért
2s1+3s2<(a+2d)2t⋅n.(3)

Az a oldalú négyzetben levő csomópontokban található szögek tartalmazzák a négyzetben levő K számú sokszög összes szögét és a benyúlók néhány szögét. Ezért a csomópontokban található szögek összege vagy nagyobb a négyzetben teljesen benn levő n-szögek szögeinek összegénél vagy egyenlő avval. Az elsőfajú csomókban 180∘-nyi, a másodfajúakban 360∘-nyi szögtér van, másrészt az n-szög szögeinek összege (n-2)⋅180∘, így
s1⋅180∘+s2⋅360∘≥K(n-2)⋅180∘.(4)
Osszuk egyenlőtlenségünket 180∘-kal és írjuk K helyett a (2) jobb oldalán álló kifejezést. Így nyilván
(n-2)(a-2d)2t<s1+2s2.

Avégett, hogy a jobb oldalon (3)-hoz hasonlóan 3s2 álljon, szorozzuk meg a egyenlőtlenséget 3/2-del, majd írjuk s1 így adódó 3/2 együtthatója helyére a nagyobb 2 értéket:
32⋅(n-2)⋅(a-2d)2t<32s1+3s2≤2s1+3s2.
Ezt (3)-mal egybevetve olyan egyenlőtlenséget kapunk, amelyben lényegében már csak a, d és n szerepel:
32⋅(n-2)⋅(a-2d)2t<(a+2d)2t⋅n.
Innen szorzással, rendezéssel, majd a pozitív n-6-tal való osztás útján
(n-6)(a2+4d2)<(20n-24)ad,a2+4d2<20n-24n-6ad,


a bal oldalról a pozitív 4d2-et elhagyva és a-val osztva
a<20n-24n-6⋅d.
Végül, mivel a jobb oldali első tényezőre
20n-24n-6=20+96n-6≤20+96=116,
azért
a<116d.
Ez azt jelenti, hogy a d-nél 116-szor nagyobb oldalú négyzetet már nem lehet n≥7 oldalú sokszöggel lefedni, és éppen ezt akartuk bizonyítani. Tehát az V. tétel valóban fennáll.
A bizonyításban a feltevéseknél jóval kevesebbet használtunk fel. A sokszögek konvex voltát csak annyiban, hogy nincs olyan másodfajú csomópont, melyben csak két csúcs esnék egybe, vagyis ahol a 360∘-os szögteret csak két csúcs töltené ki. Nem használtuk ki a sokszögek egybevágóságát sem, csak azt, hogy területük egyenlő, és van olyan kör, amellyel a parkettázs valamennyi sokszöge lefedhető.
Nem szabatosan, de szemléletes fogalmazásban a bizonyítást a következőképpen vázolhatjuk. Egy elsőfajú csomóban legalább két csúcs esik egybe, és ezért a csomó 180∘-os szögterében a fedőidomoknak legalább két szöge helyezkedik el. Így egy szögre ,,átlagban'' legfeljebb 180∘/2=90∘ jut. Hasonlóan a másodfajú csomókba befutó szögekre ,,átlagban'' legfeljebb 360∘/3=120∘ jut. Ezek azt jelentik, hogy az n oldalú fedősokszögek ,,átlagos'' szöge nem lehet nagyobb 120∘-nál, vagyis
(n-2)⋅180∘n≤120∘,
és innen
n≤6.
Ha tehát n≥7 lenne, akkor a fedősokszögek szögei ,,nem férnének el'' a csomópontokban rendelkezésre álló szögterekben. ‐ Az a oldalú négyzettel tulajdonképpen akkora területet kerestünk, melyen a kiegyenlítődések ellenére is kitűnik az ellentmondás.
1 A szerzőnek a budapesti Ifjúsági Matematikai Körben 1960. január hóban tartott előadása

2Ezt a tételt Kárteszi Ferenc tűzte ki feladatként, Mat. és Fiz. Lapok 50 (1943) 370. o., 21. feladat. Megoldása a lap megszűnése miatt nem jelent meg.