Kezdőlap


Cím:	A burkológörbékről
Szerző(k):	Vermes Miklós
Füzet:	1960/december, 225 - 227. oldal	PDF \| MathML
Témakör(ök):	Szakmai cikkek

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Ebben a cikkben egy példával kapcsolatban olyan fogalmat ismerünk meg, amely tulajdonképpen a felsőbb matematikába tartozik, mégis hozzáférhető egyszerű eszközökkel.
Adott $A$ pontból meghatározott $c$ kezdősebességgel történő ferde hajítással, el kell találni egy meghatározott helyzetű $B$ pontot. Milyen $α$ szöggel történjék a hajítás?

B

pont helyzetét

x = A C

és

y = C B

koordinátái határozzák meg. Az elhajított tárgy helyzetét, mint az idő függvényét a ferde hajítás közismert törvényei alapján ezek a képletek adják meg:

\begin{matrix} x = c cos α \cdot t, \\ y = c sin α \cdot t - \frac{g}{2} \cdot t^{2} . \end{matrix}

t

idő kiküszöbölésével kapjuk a pálya függvényeit:

\begin{matrix} y = tg α \cdot x - \frac{g}{2 c^{2} cos^{2} α} \cdot x^{2} . \end{matrix}

Célszerű rövidítő jelölésként vezessük be az

F = \frac{c^{2}}{2 g}

mennyiséget, a függőleges felfelé hajítás magasságát. Ezt használva

\begin{matrix} y = tg α \cdot x - \frac{1}{4 F cos^{2} α} \cdot x^{2} . \end{matrix}

Feladatunk azon

α

szög megkeresése, amely mellett a

c

kezdősebességgel elhajított tárgy eltalálja

B

pontot. Ebben az esetben a pályát jellemző függvényben

x

és

y

jelentik a megadott

B

pont koordinátáit,

α

pedig az ismeretlen. Felhasználva az

\frac{1}{cos^{2} α} = 1 + {tg}^{2} α

azonosságot

\begin{matrix} y = tg α \cdot x - \frac{1}{4 F} \cdot (1 + {tg}^{2} α) x^{2} . \end{matrix}

Ezt az egyenletet

tg α

szerint rendezzük:

\begin{matrix} x^{2} {tg}^{2} α - 4 F x \cdot tg α + (4 F y + x^{2}) = 0. \end{matrix}

Megoldjuk

tg α

-ra, és megkapjuk a

B

pont eltalálásához szükséges szöget:

\begin{matrix} tg α = \frac{2 F \pm \sqrt[]{4 F^{2} - 4 F y - x^{2}}}{x} . \end{matrix}

Lássunk egy számpéldát. Legyen

c = 28 m / sec

g = 980 cm / {sec}^{2}

, ekkor

F = 40 m

. Az eltalálandó

B

pont koordinátái legyenek

x = 50 m

y = 21, 875 m

. Ekkora megoldóképlet alapján:

\begin{matrix} tg α = 1, 6 \pm 0, 4, & tg α_{1} = 1, 6 + 0, 4 = 2, & α_{1} = 63^{\circ} 26', \\ tg α_{2} = 1, 6 - 0, 4 = 1, 2, & α_{2} = 50^{\circ} 12' . \end{matrix}

Tehát adott sebesség mellett

B

pont két röppályán található el, amelyek közül az egyik laposabb, és ezen rövidebb idő alatt ér az elhajított tárgy a

B

pontba, a másik pálya meredekebb, ezen később ér

B

-be az elhajított tárgy. Ezt a fizikai körülményt, hogy megadott sebességgel két pályán érhető el

B

pont, az tükrözi vissza, hogy egyenletünknek két megoldása van.
Más a helyzet, ha a célba vett pont másutt van. Legyen például ugyanazon

c = 28 m / sec

sebesség mellett

x = 5000 m

y = 4000 m

. Az adatokra ránézve azonnal feltűnik, hogy itt valami nincs rendben: ilyen messze levő célpont ezzel a sebességgel nem található el. Kiderül ez az egyenlet oldóképletéből is, amelyben a négyzetgyök alatti mennyiség ekkora

x

és

y

mellett negatív.
Ha tehát adott

c

sebességgel hajítunk a legkülönbözőbb irányokba, akkor a tér pontjai két csoportba oszthatók. Vannak olyan pontok, amelyek két hajítási pályán is eltalálhatók (ilyenkor egyenletünk oldóképletében a négyzetgyök alatti mennyiség pozitív). De vannak olyan pontok is, amelyek a megadott elhajítási sebesség mellett semmiféle módon sem érhetők el (ekkor a gyökjel alatti mennyiség negatív). A függőleges sík (a tér) pontjai két tartományra oszlanak: a kétféle pályán eltalálható és az egyáltalán el nem érhető pontok összességére. Ez a két tartomány valahol, egy görbe mentén határos. Ha olyan pontot választunk ki, amely a határoló görbe mentén fekszik, és ennek koordinátáit helyettesítjük a megoldóképletbe, akkor a gyökjel alatti mennyiség nulla:

\begin{matrix} 4 F^{2} - 4 F y - x^{2} = 0. \end{matrix}

Az egyenletnek ilyenkor csak ez az egy megoldása van: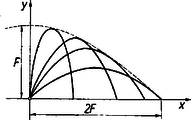

\begin{matrix} tg α = \frac{2 F}{x} . \end{matrix}

Tehát a

4 F^{2} - 4 F y - x^{2} = 0

egyenlet olyan

x

y

koordinátájú pontokat választ ki, amelyek csak egyféle pályán érhetők el. Az egyenlet rendezve:

\begin{matrix} y = F - \frac{1}{4 F} \cdot x^{2} . \end{matrix}

Ez a görbe olyan parabolát jelent, amely az

y

tengelyt

F

, az

x

tengelyt

\pm 2 F

távolságban metszi, és fókusza az origóban van. Neve burkológörbe. Adott kezdősebességű hajításokat tekintve ezen vannak azok a legmesszebb fekvő pontok, amelyek a hajítással elérhetők, és ezek a pontok csak egyetlen hajítási pályával érhetők el.

Valamennyi (adott

c

kezdősebességű, különböző indulási szögű) hajítási pálya belülről érinti a burkológörbét. Természetesen ugyanez a helyzet valamennyi, az

y

tengelyen átmenő függőleges síkban: a burkoló parabolák forgás felületet, forgási paraboloidot alkotnak. Ezt ismerve sok feladatot igen gyorsan tudunk megoldani. Például a legnagyobb hajítási távolságot a burkolófelületnek az

x

tengellyel való metszéspontja jelöli meg. Ekkor a célpont

x

koordinátája

x = 2 F

és az ehhez a pályához tartozó elhajítási szög

tg α = \frac{2 F}{x}

alapján:

tg α = \frac{2 F}{2 F} = 1

, így

α = 45^{\circ}

.
A burkológörbe szerepéről lássunk még egy példát. Adva van egy vízzel telt edény, függőleges oldalfalakkal. A víz felszíne alatt milyen mélységben

(h)

kell lyukat nyitnunk, hogy a vízszintes hajítás törvénye szerint kiömlő vízsugár eltalálja a megadott helyzetű,

x

y

koordinátájú

B

pontot?
Egyszerűség kedvéért helyezzük az origót az edény oldalfalához, a víz felszínére, és az

y

tengelyt irányítsuk lefelé.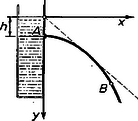

h

mélységből

c = 2 g h

sebességgel ömlik ki a víz és

t

másodperc alatt

x = c t

távolságra,

y = \frac{g}{2} \cdot t^{2} + h

mélységre jut el. A vízsugár ugyanis

h

mélységben indul el, és ehhez kell hozzáadni az esés útját.

t

kiküszöbölésével kapjuk a hajítási pálya függvényét:

\begin{matrix} t = \frac{x}{c}, y = \frac{g}{2} \cdot {(\frac{x}{c})}^{2} + h, y = \frac{g}{2 c^{2}} \cdot x^{2} + h . \end{matrix}

Felhasználva a kezdő sebesség

c = \sqrt[]{2 g h}

értékét:

\begin{matrix} y = \frac{1}{4 h} \cdot x^{2} + h . \end{matrix}

A pálya függvényéből kiesik

g

; az edényből kiömlő víz pályái a Holdon is ugyanazok volnának. Ennek oka: kisebb

g

esetén a gravitáció kisebb mértékben görbíti lefelé a parabolát, viszont kisebb a kezdő sebesség is.
A mi feladatunkban az a kérdés, adott

x

y

koordinátájú

B

pont eltalálásához milyen mélyen nyissunk lyukat az edényen? Egyenletünket adott

x

y

mellett

h

-ra kell megoldanunk. Rendezve:

\begin{matrix} 4 h^{2} - 4 y h + x^{2} = 0. \end{matrix}

Ennek megoldása

\begin{matrix} h = \frac{y \pm \sqrt[]{y^{2} - x^{2}}}{2} . \end{matrix}

Ismét két megoldás adódik, kétféle lyukmélység mellett találja el a vízsugár a

B

pontot. A burkológörbén fekvő pontok

x

y

koordinátáinak összefüggését a négyzetgyök alatti mennyiség eltűnése szolgáltatja:

\begin{matrix} y^{2} - x^{2} = 0. \end{matrix}

Innen

y = x

. Tehát a burkológörbe

45^{\circ}

-ban lefelé haladó egyenes.
Gondolatmenetünk egyszerű eszközökkel vezetett el a burkológörbe fogalmához, ez pedig elősegíti egyes feladatok megoldását. (Lásd a közölt ide tartozó feladatot!)