Kezdőlap


Cím:	A forgómozgásról. Centrifugális és Coriolis-erők
Szerző(k):	Holics László
Füzet:	1960/november, 161 - 166. oldal	PDF \| MathML
Témakör(ök):	Szakmai cikkek, Mozgásegyenletek gyorsuló koordináta-rendszerekben

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Tengelye körül méltóságteljesen forgó Földünk nem sok meglepetéssel bosszantja a mindennapi életben azokat, akik a legkülönbözőbb szélességi és hosszúsági fokokon azzal a feltevéssel végzik méréseiket, hogy a Newton-törvényeknek megfelelő inerciarendszerben vannak. Csak akkor kerülnek felszínre a Föld forgásának ,,furcsa'' következményei, ha rendkívül pontos méréseket kell végezni, vagy ha nagy távolságok és sebességek lépnek fel a folyamatokban.
A Foucault-inga állandóan változtatja lengési síkját, a függőón nem pontosan a gravitációs erő irányába mutat, a testek súlya más az Egyenlítőn, mint a sarkokon, az északról dél felé folyó folyók jobb partjukat jobban kimossák, mint a balt, a magasból leeső kő kelet felé esik, eltérve a függőlegestől, a tüzérségi lövedék ballisztikus pályája a Földhöz viszonyítva nem síkgörbe...
Vizsgáljuk meg, mi az oka ezeknek a ,,szokatlan'' jelenségeknek.

Tehetetlenségi erők

Ha valakinek módjában lenne ég és Föld között, az állócsillagokhoz képest egyenesvonalú pályán egyenletes sebességgel és egy Newton-féle mechanikai tankönyvvel a kezében lebegni és a földi eseményeket figyelemmel kísérni, az általunk furcsának ítélt jelenségeket éppen a legszabályosabbaknak, a dinamika törvényeinek pontosan megfelelőeknek találná. A tüzérségi lövedék pályáját síkgörbének látná, a magasból leeső kő számára nem sietne kelet felé, mindössze megtartaná a vonzóerő irányára merőleges sebességkomponensét (I. törvény), a Foucault-inga is megtartaná lengési síkját, mindössze a Föld fordulna el alatta stb. Visszatérve a Földre, hősünk ismét kénytelen lenne tapasztalni a fentebb említett ,,furcsaságokat'', röviden azt, hogy a Földön a folyamatok a dinamika Newton-féle tankönyveitől eltérően mennek végbe. Mindennek az oka a Föld forgásában keresendő. Bár a lassú forgás miatt ezek a hatások kicsik, mégis bizonyos esetekben számottevőek. Emberünk rövid, de logikus gondolkodás után arra a következtetésre kénytelen jutni, hogy két lehetőség között kell választania. Vagy azt mondja, hogy nem a Newton-féle törvényeknek megfelelő ún. ,,inerciarendszerben'' van (vagyis olyanban, amilyenre Newton törvényeit vonatkoztatta, amelyben pl. a magára hagyott test egyenesvonalú, egyenletes mozgást végez), hanem ettől eltérő ,,rossz'' rendszerben, s ezért itt nem érvényesek a dinamika törvényei, vagy pedig elfogadja, hogy vonatkoztatási rendszere jó, a Newton-törvények is helyesek, csak ‐ hogy ellentmondásba ne kerüljön ‐ kénytelen feltételezni olyan, az inerciarendszerekben nem működő erőket, amelyeket hozzávéve a testre ható összes erőkhöz, a Newton-törvények ismét helyesen adják a mozgások leírását. Hősünkkel együtt ezt a második választási lehetőséget követjük, és a tapasztalattal egyezésben ezeknek az erőknek a fellépését a testek tehetetlenségének és a rendszer gyorsulásának (pl. forgásának) tulajdonítjuk. Ezek az erők okozzák hát a bevezetőben említett ,,szokatlan'' jelenségeket. Érthető okok miatt ezeket az erőket tehetetlenségi vagy inercia-erőknek nevezzük. Nagyon fontos, hogy világosan lássuk a különbséget a ,,valódi'' vagy ,,Newton-féle erők" és a tehetetlenségi vagy inercia-erők között. Amíg egy testre ható ,,Newton-féle erőnek'' fellépte egy másik test jelenlétét feltételezi, amellyel az kölcsönhatásban áll, addig a tehetetlenségi erő nem valamilyen másik testből származik, hanem kizárólag a szóbanforgó test tehetetlenségének és a vonatkoztatási rendszer gyorsulásának a következménye.
A továbbiakban azt fogjuk megvizsgálni, hogy milyen tehetetlenségi erők lépnek fel az egyenletesen forgó rendszerekben olyan megfigyelő szempontjából, aki a rendszerrel együtt forog. (Ilyen pl. Földünk a rajta levő megfigyelőkkel, ha koordináta-rendszerüket földi környezetükhöz rögzítik.)

A centrifugális erő

A körpályán mozgó, ill. forgómozgást végző testeken fellépő centrifugális erőt mindenki ismeri, legalábbis tapasztalatból. A középiskolában találkozik az erő kifejezésének részletes levezetésével is. Tehetetlenségi erő. Ha a villamos kanyarodik, ez az erő lép fel a bennülőkön, és nyomja a kocsi oldalának őket. A kocsi falának rugalmas ereje szolgáltatja a centrifugális erő reakcióerejét. Ez utóbbi nem tévesztendő össze a centripetális erővel. A centripetális erő fogalmának és elnevezésének létjogosultsága kizárólag nyugvó, külső megfigyelő szempontjából van, aki egy a középpont felé mutató valódi, Newton-féle erőt feltételez, mely a testet tehetetlenségi pályájának megváltoztatására kényszeríti. Ennek reakcióját nem mondjuk centrifugális erőnek, hanem külön név nélkül, mint reakcióerőt tartjuk számon.

a) b)
1. ábra

Látjuk, hogy az elnevezések mennyire következetesek: különbséget tesznek a koordináta-rendszer választások között, és határozottan vagy belső, együtt forgó, vagy külső, álló megfigyelőre utalnak. (L. 1. a) és b) ábrákat.)
A centrifugális erő kifejezése a test tömege, tengelytől való távolsága és a szögsebesség függvényében:

\begin{matrix} P_{c} = m \cdot r \cdot ω^{2} . \end{matrix}

Ez a tömeggel arányos erő lép fel minden olyan testen, amely egy

ω

szögsebességgel forgó koordináta-rendszerhez képest nyugszik. Gondoljuk végig, a fent felsorolt jelenségek közül melyek magyarázhatók a centrifugális erőkkel. A centrifugális erő megnövekedésével magyarázható a nyugatról keletre haladó testek súlyának csökkenése is (Eötvös-effektus). Ekkor a testhez rögzített koordináta-rendszer szögsebessége a Földéhez képest megnövekszik

ω' = v / r

értékkel, s a rendszer szögsebességváltozása centrifugális erő növekedést, azaz súlycsökkenést hoz létre.

A Coriolis-erő

Ha a kiszemelt test nyugszik forgó rendszerünkben, rajta más tehetetlenségi erő nem lép fel. Nem ilyen egyszerű a helyzet azonban akkor, ha a test a forgó koordinátarendszerhez képest mozog, pl. a forgó korongon annak széle felé halad. Az alábbiakban részletesen megvizsgáljuk forgó rendszerben a rendszerhez képest mozgó testekre gyakorolt olyan erőhatásokat, amelyek csakis a rendszer gyorsulásának és a test tehetetlenségének következményei. Számításainkat olyan egyszerű esetre végezzük el, amelyben egyenletes szögsebességgel forgó koordináta-rendszert veszünk alapul, s a hozzá képest mozgó test csak sugárirányú, egyenletes sebességű mozgást végez.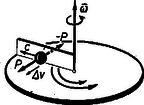

2. ábra

Első pillanatban látszik, hogy ha egy testet, amely sugár irányban pl. kifelé halad, arra kényszerítünk, hogy megtartsa szögsebességét (pl. egy súrlódás nélküli merev, sugárirányú fallal, l. a 2. ábrát), a centrifugális erő (

m r ω^{2}

) megnövekszik. Ezen kívül azonban nyilván fel kell lépnie egy másik erőnek is, amely a test kerületi sebességének a sugárral arányos növekedését biztosítja (ezt képviseli a fal), s ugyanakkor egy reakcióerőnek, amely a sugármenti falra visszahat. Ezt a kényszererőt, s a vele kapcsolatos reakcióerőt amelyet Coriolis-erőnek neveznek ‐ vesszük vizsgálat alá. (Ha a testet nem kényszeríti egy fal szögsebességének megtartására, miközben kifelé halad, nyilván lemarad az induló sugárhoz képest, mégpedig a rendszerhez viszonyítva gyorsulva, amit a külső szemlélő természetes, erőmentes állapotnak tart, míg az együtt forgó megfigyelő ezt a fennálló Coriolis-erőnek tulajdonítja.)
A fellépő erő irányát ebben az esetben azonnal meghatározhatjuk, hiszen a fal, mint kényszerfelület saját irányára merőleges erőt gyakorol a testre, tehát az erő merőleges a testnek a rendszerhez viszonyított haladási sebességére ! Miután a Coriolis-erő (és természetesen a Coriolis-gyorsulás) irányát meghatároztuk, próbáljuk meghatározni annak nagyságát is. Egyik kínálkozó módszer annak a kényszererőnek a kiszámítása, amelyet a sugárirányú fal okoz a test kerületi sebességének egyenletes növelése közben.
Tegyük fel tehát, hogy a test sugár irányban egyenletes

c

sebességgel halad a forgó rendszerhez képest. Ekkor a kerületi sebesség,

v = r \cdot ω

egyenletesen változik a sugár növekedésével, vagyis a fellépő gyorsulás állandó. Tekintsük a forgó korongot és a rajta levő testet egy rendszernek. A rendszer nyilván nem zárt, mert a szögsebesség megtartásához állandóan ható külső forgatónyomatékra van szükség. Alkalmazzuk a forgómozgásnál érvényes impulzusnyomaték-tételt: az impulzusnyomaték

(F t)

egyenlő a mozgásmennyiségnyomaték megváltozásával

(Δ I ω)

(l. XX. kötet 3‐4. számban a forgómozgásról megjelent cikkünket).
Mivel a korong szögsebessége nem változik, az itt szereplő mozgásmennyiségnyomaték megváltozás csak a sugárirányban mozgó testre korlátozódik (érvényes az additivitás), s így

F t = I_{2} ω - I_{1} ω

.
Ha a forgatónyomaték helyébe a fellépő erő és karjának szorzatát írjuk, épp a Coriolis-erő ellenerejét kapjuk kifejezésünkben. Itt azonban figyelembe kell vennünk, hogy a forgatónyomaték egyenletesen növekszik, ezért a kezdő és végérték számtani közepével kell számolnunk (átlag):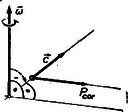

\begin{matrix} P_{cor} \cdot \frac{R + r}{2} \cdot t = I_{1} ω - I_{2} ω = m (R^{2} - r^{2}) \cdot ω = m (R + r) (R - r) \cdot ω, \end{matrix}

ahonnan:

\begin{matrix} P_{cor} = 2 m \frac{R - r}{t}, vagy \frac{R - r}{t} = c \end{matrix}

helyettesítéssel:

\begin{matrix} P_{cor} = 2 m c ω és a_{cor} = 2 c \cdot ω . \end{matrix}

Ezek szerint a Coriolis-erő egyenesen arányos a forgás szögsebességével, a mozgó test sebességével és tömegével. Itt a Coriolis-erő abszolút-értékét számítottuk ki. Iránya merőleges mind a szögsebesség-vektor irányára (tengely irány), mind a

c

sebesség irányára, s a szögsebességgel

(ω)

, valamint a rendszerhez viszonyított haladási sebességgel

(\vec{c})

balrendszert alkot, vagyis az

[\vec{ω}, \vec{c} [

síkra merőlegesen felmérve, irányából visszanézve

\vec{ω}

-t

\vec{c}

-be negatív forgás viszi át. (3. ábra.)

3. ábra

Fenti eredményünkből azonnal látszik, hogy a Földön haladó testeken miért lépnek fel azok az eltérítő hatások, amelyeket említettünk, ha a forgó rendszerhez képest mozgó test sebessége a forgástengelyre, merőleges irányú komponenst is tartalmaz. Az északról délre folyó folyó egyre nagyobb sugarú körön, tehát egyre nagyobb kerületi sebességgel kényszerül együtthaladni a Földdel, így tehetetlenségénél fogva medrének jobb partját jobban kikezdi, mint a balt. (A déli félgömbön ellenkező a helyzet.) A magasról leejtett kő fenti kerületi sebessége nagyobb, mint a földfelszín sebessége, így kerületi sebességét megtartva a Föld forgásának irányában ,,előre'' esik. A földi megfigyelő ezt a vízszintes gyorsulást a Coriolis-erőnek tulajdonítja.
A következőkben megadjuk a Coriolis-erőnek levezetését olyanok számára, akik még nem ismerik a forgómozgásnál szereplő nyomatékok fogalmát. Csak a szögsebesség

(ω = a / t)

ismeretét tételezzük fel.
Egyenletes szögsebességgel forgó korongon gurítsunk ki sugárirányban, egyszerűség kedvéért a középpontból

(r = 0) c

kezdősebességgel súrlódás nélküli golyót. Tekintve, hogy a golyó és a korong között semmilyen mechanikus kapcsolat nincs, a golyó nyilván lemarad az induló sugárhoz képest, s mire a középponttól

R

távolságba ér, a körív irányában

R a

utat tesz meg.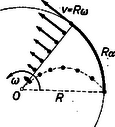

4. ábra

Mivel a koronghoz viszonyított ,,lemaradási'' (kerületi) sebességének változása egyenletes ‐ a kerületi sebesség az egyenletesen változó sugárral arányos ‐ a fellépő erő és ezzel együtt a gyorsulás is állandó. Ebből következik, hogy az erő irányában megtett

R a

út megtételére érvényes a négyzetes úttörvény, azaz

a = ω t

helyettesítéssel írhatjuk egyrészt:

s = R a = R ω t

, másrészt:

\begin{matrix} s = a_{cor} t^{2} / 2. \end{matrix}

A kettőt összehasonlítva:

\begin{matrix} R ω t = \frac{a_{cor} t^{2}}{2} és a_{cor} = \frac{2 R ω}{t} . \end{matrix}

Ha meggondoljuk, hogy

R / t

a sugárirányban megtett út és a megtételéhez szükséges idő hányadosa éppen a sugárirányú egyenletes sebességet adja

(c)

, a Coriolis-gyorsulásra kapjuk:

\begin{matrix} a_{cor} = 2 c ω és a Coriolis-erő: P = 2 m c ω . (L. a 4. ábrát.) \end{matrix}

Alkalmazások

Eredményeinket felhasználva vizsgáljuk meg néhány példán, hogy milyen és nagyságrendileg mekkora hatások lépnek fel a Föld forgása következtében a rajta mozgó testeken.
1. Középnehéz tüzérség a 45. szélességi fokon tőle dél felé kb. 20 km-re fekvő célpontot akar megsemmisíteni. Milyen irányban és mennyire kell eltérnie a löveg csőtengelyének a lövegen és célponton átfektetett függőleges síktól, hogy pontosan a célba találjon ? (Ennyivel térne el a lövedék, ha ,,pontosan'' a célra irányoznák a löveget.) A lövedék sebessége

800 {msec}^{-} 1

. (Tekintsük a lövést közelítőleg vízszintes hajításnak, s a közel egyenes pálya mentén a

v

sebességet állandó irányúnak és nagyságúnak.) Esetünkben az elhanyagolás nem nagy.
Az igen kis lőtávolság miatt feltételezhetjük, hogy e szakaszon a Föld síkkal helyettesíthető, s így a sebesség radiális komponensét végig állandónak vehetjük. Számítsuk ki a Coriolis-gyorsulást. Adatok: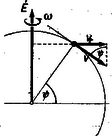

v = 800 {msec}^{-} 1

ψ = 45^{\circ}

s = 20 km

5. ábra

Az 5. ábra szerinti sebességfelbontás értelmében

v_{r} = v \cdot sin ψ

. A gyorsulás értéke tehát:

2 v ω \cdot sin ψ

, vagyis

a_{cor} = 2 \cdot 800 \cdot sin 45^{\circ} \cdot 7, 29 \cdot 10^{- 5} {msec}^{- 2} = 0, 08223 {msec}^{- 2}

, ahol a Föld forgásából eredően koordináta-rendszerünk szögsebessége:

ω = 2 π / T = 7, 29 \cdot 10^{- 5} {sec}^{- 1}

T = 861 64 sec

, vagyis egy csillagnap, mert az állócsillagokhoz kell viszonyítani az inerciarendszer tengelyeit ! A sugárirányra merőleges eltérés

s = a_{cor} \cdot t^{2} / 2

, ahol

t = 20 000 : 800 sec = 25 sec

, s így

s = \frac{1}{2} 0, 08223 {msec}^{- 2} \cdot 25^{2} {sec}^{2} \sim 25, 7 m

, vagyis

25, 7

méter ! Ennyivel kell kelet felé célozni, hogy a ,,lemaradó'' lövedék épp eltalálja a célt.

25, 7

méteres ívhez 20 000 m-es sugáron

a = 0, 00128 radián = 0, 073^{\circ}

, vagy bevezetve a tüzérségi vonást (a körív 6000-ed részéhez tartozó középponti szöget)

a = 1, 2

vonás eltérés tartozik.

2. Forgózsámolyon álló kísérletező kezében 5‐5 kg-os tömegeket tartva karjait kinyújtja. A forgózsámoly

n = 0, 8 {sec}^{- 1}

fordulatszámmal forog. A kísérletező karjait hirtelen,

v = 2 {msec}^{- 1}

sebességgel maga felé behúzza. Mekkora erő hat a súlyokra, amelynek hatására a kerületi sebesség irányában felgyorsulnak, vagy mekkora erőt kell kifejtenie a kísérletezőnek, hogy a súlyok szögsebességét ne engedje megváltoztatni ? (Gondoskodnunk kell a forgózsámoly nagy tehetetlenségi nyomatékáról, vagy állandó külső erőről.)

\begin{matrix} P = m \cdot a_{cor} = 2 m v ω = 2 \cdot 5 kg \cdot 2 {msec}^{- 1} \cdot 2 π \cdot n \end{matrix}

Ha meggondoljuk, hogy a centrifugális erő is növeli az eredőt, láthatjuk, hogy komoly hatások lépnek fel a gyorsuló rendszerekben a bennük mozgó testekre.
Befejezésül megjegyezzük, hogy a Coriolis-erő általánosabb levezetése szerint annak értéke:

P_{cor} = 2 m v ω sin ϑ

, ahol

ϑ =

\vec{v}

és

\vec{ω}

(tengely) által bezárt szög. Ebből láthatjuk, hogy ez az erő a rendszerhez képest bármely irányban mozgó testnél fellép, csak akkor nem, ha a sebesség párhuzamos a forgástengellyel

\vec{(ω)}

.
Kiegészítésül felírjuk, hogy egy általánosan mozgó koordináta-rendszerben egy benne mozgó tömegpontra milyen erők hatnak. Általános esetben 5-féle erő hat. Ezek közül az egyik a környező testektől származó Newton-féle erők eredője, a többi különböző tehetetlenségi erő;
1) magának a rendszernek az inerciarendszerhez viszonyított transzlációs gyorsulásából, 2) a centrifugális gyorsulásból, 3) a pontnak a rendszerhez viszonyított sebessége következtében fellépő Coriolis-gyorsulásból és végül 4) a rendszer szöggyorsulásából, ill. a szögsebesség nagyság, vagy irányváltozásából (tengelyirány változásból) származó erő.
A Newton-féle valódi erő az inerciarendszerben érvényes II. törvény szerint:

P = m \cdot a

. A rendszer gyorsulása miatt fellépő tehetetlenségi erők összege:

P_{i} = m \cdot a_{t r} + m \cdot r \cdot ω^{2} + 2 m v ω \cdot sin ϑ + m \cdot r \frac{Δ ω}{Δ t}

. A gyorsuló koordináta-rendszerünkben is érvényes II. törvény alakja (a fellépő inerciaerők figyelembevételéből):

P' = P + P_{i}

, azaz

P' = P + m (a_{t r} + r ω^{2} + 2 v ω \cdot sin ϑ + r \frac{Δ ω}{Δ t})

, vagy, ha a Newton-féle valódi erő által létrejött inerciarendszerhez viszonyított gyorsulást

a

-val jelöljük, akkor

P' = m (a + a_{t r} + r ω^{2} + 2 v ω sin ϑ + r \frac{Δ ω}{Δ t})

. Itt természetesen minden tagnál az irányokat is figyelembe kell venni (vektori összeg) ! Ebből is látszik, hogy pl. az űrhajózás navigációs problémái mennyi, sokszor egyidejűleg fellépő hatás figyelembevételéből erednek.